- •1.Предел функции. Теоремы о пределах.
- •2.Непрерывность функции. Точки разрыва функции
- •3. Производная функции в точке. Правила, дифференцирования.
- •4.Производная сложной и обратной функции.
- •5.Геометрический и физический смысл производной.
- •6.Монотонность функции. Экстремумы функции.
- •8.Асимптоты.
- •Частные производные. Примеры решений
- •10.Производная сложной и неявной функции двух переменных
- •11.Использование частных производных в геометрии.
- •12.Экстремумы функции двух переменных.
1.Предел функции. Теоремы о пределах.
Преде́л фу́нкции (предельное значение функции) в заданной точке, предельной для области определения функции, — такая величина, к которой стремится рассматриваемая функция при стремлении её аргумента к данной точке.
Предел функции является обобщением понятия предела последовательности: изначально под пределом функции в точке понимали предел последовательности элементов области значений функции, составленной из образов точек последовательности элементов области определения функции, сходящейся к заданной точке (предел в которой рассматривается); если такой предел существует, то говорят, что функция сходится к указанному значению; если такого предела не существует, то говорят, что функция расходится.
Теорема 1. (о предельном переходе в равенстве) Если две функции принимают одинаковые значения в окрестности некоторой точки, то их пределы в этой точке совпадают.
![]() Þ
Þ ![]()
![]() .
.
Теорема 2. (о предельном переходе в неравенстве) Если значения функции f(x) в окрестности некоторой точки не превосходят соответствующих значений функции g(x) , то предел функции f(x) в этой точке не превосходит предела функции g(x).
![]() Þ
Þ ![]()
![]() .
.
Теорема 3. Предел постоянной равен самой постоянной.
![]() .
.
Доказательство. f(x)=с, докажем,
что ![]() .
.
Возьмем произвольное e>0. В качестве d можно взять любое
положительное
число. Тогда при ![]()
![]() .
.
Теорема 4. Функция не может иметь двух различных пределов в
одной точке.
Доказательство. Предположим противное. Пусть
![]() и
и ![]() .
.
По теореме о связи предела и бесконечно малой функции:
f(x)-A=![]() -
б.м. при
-
б.м. при![]() ,
,
f(x)-B=![]() -
б.м. при
-
б.м. при![]() .
.
Вычитая эти
равенства, получим:![]()
B-A=![]() -
-![]() .
.
Переходя к пределам
в обеих частях равенства при ![]() ,
имеем:
,
имеем:
B-A=0, т.е. B=A. Получаем противоречие, доказывающее теорему.
Теорема 5. Если
каждое слагаемое алгебраической суммы
функций имеет предел при ![]() ,
то и алгебраическая сумма имеет предел
при
,
то и алгебраическая сумма имеет предел
при![]() ,
причем предел алгебраической суммы
равен алгебраической сумме пределов.
,
причем предел алгебраической суммы
равен алгебраической сумме пределов.
![]()
![]()
![]()
![]() .
.
Доказательство. Пусть ![]() ,
,![]() ,
,![]() .
.
Тогда, по теореме о связи предела и б.м. функции:
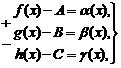 где
где ![]() -
б.м. при
-
б.м. при![]() .
.
Сложим алгебраически эти равенства:
f(x)+g(x)-h(x)-(А+В-С)=![]() ,
,
где ![]() б.м.
при
б.м.
при![]() .
.
По теореме о связи предела и б.м. функции:
![]() А+В-С=
А+В-С=![]()
![]()
![]() .
.
Теорема 6. Если
каждый из сомножителей произведения
конечного числа функций имеет предел при ![]() ,
то и произведение имеет предел при
,
то и произведение имеет предел при![]() ,
причем предел произведения равен
произведению пределов.
,
причем предел произведения равен
произведению пределов.
![]()
![]()
![]() .
.
Следствие. Постоянный множитель можно выносить за знак предела.
![]()
![]()
![]() .
.
Теорема 7. Если
функции f(x) и g(x) имеют
предел при ![]() ,
,
причем ![]() ,
то и их частное имеет предел при
,
то и их частное имеет предел при![]() ,
причем предел частного равен частному
пределов.
,
причем предел частного равен частному
пределов.
 ,
, ![]() .
.
2.Непрерывность функции. Точки разрыва функции
Непрерывная функция — функция без «скачков», то есть такая, у которой малые изменения аргумента приводят к малым изменениям значения функции.
Непрерывная функция, вообще говоря, синоним понятия непрерывное отображение, тем не менее чаще всего этот термин используется в более узком смысле — для отображений между числовыми пространствами, например, на вещественной прямой. Эта статья посвящена именно непрерывным функциям, определённым на подмножестве вещественных чисел и принимающим вещественные значения.
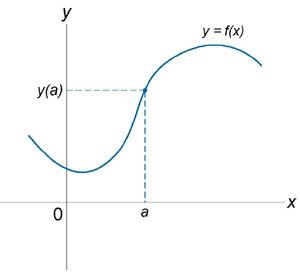
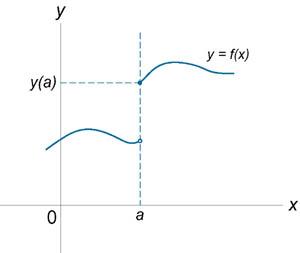
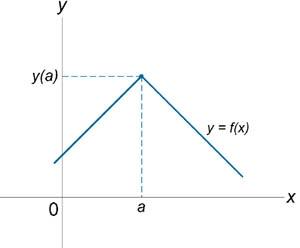
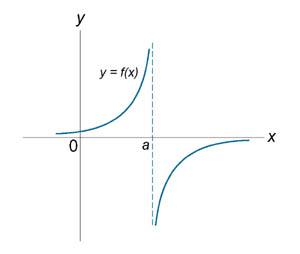
Если функция f (x) не является непрерывной в точке x = a, то говорят, что f (x) имеет разрыв в этой точке. На рисунке 1 схематически изображены графики четырех функций, две из которых непрерывны при x = a, а две имеют разрыв.
|
|
|
|
|
Непрерывна при x = a. |
|
Имеет разрыв при x = a. |
|
|
|
|
|
Непрерывна при x = a. |
|
Имеет разрыв при x = a. |
|
Рисунок 1. | ||
Классификация точек разрыва функции
Все точки разрыва функции разделяются на точки разрыва первого и второго рода. Говорят, что функция f (x) имеет точку разрыва первого рода при x = a, если в это точке
Существуют левосторонний предел
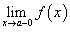 и
правосторонний предел
и
правосторонний предел 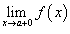 ;
;Эти односторонние пределы конечны.
При этом возможно следующие два случая:
Левосторонний предел и правосторонний предел равны друг другу:
![]()
Такая точка называется точкой устранимого разрыва.
Левосторонний предел и правосторонний предел не равны друг другу:
![]()
Такая
точка называется точкой
конечного разрыва.
Модуль разности значений односторонних
пределов![]() называется скачком
функции.
называется скачком
функции.
Функция f (x) имеет точку разрыва второго рода при x = a, если по крайней мере один из односторонних пределов не существует или равен бесконечности.