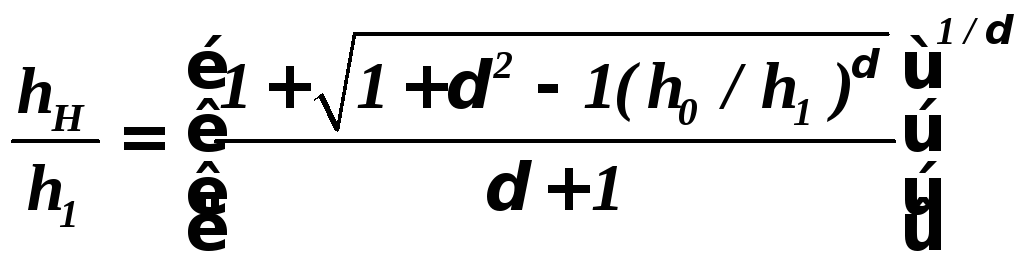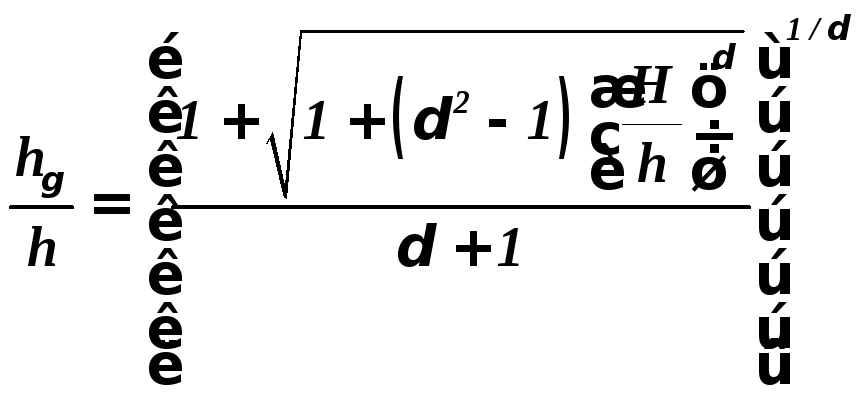18

(15.17)

Формула 15.16 получена при условии равномерной деформации по высоте и поэтому, при расчетах для случаев прокатки с < 1 дает результаты, которые отличаются от действительных. Для учета этой неравномерности Целиков А.И. рекомендует вводить коэффициент .

15.6. Формулы для определения средних нормальных напряжений

В общем случае формула для определения среднего нормального контактного напряжения имеет вид

(15.18)

где – сопротивление деформации,

– коэффициент напряженного состояния,

–коэффициент, учитывающий влияние среднего главного напряжения.

При двухмерной деформации, когда распространением можно пренебречь, = 1,15, а при прокатке со свободным уширением = 1.

Для определения в случае трехмерной деформации Зарощинский М.Л. предложил формулу

(15.19)

где ,, – логарифмические деформации.

В.С. Смирнов получил такие уравнения:

при (15.20)

при (15.21)

Коэффициент называют коэффициентом подпора. По своему физическому смыслу он показывает, насколько среднее контактное давление превышает предел текучести деформируемого металла:

(15.22)

Коэффициент напряженного состояния можно представить в виде произведения четырех коэффициентов

где – коэффициент, учитывающий изменение влияния внешнего трения в связи с уширением.

По Целикову А.И.

при (15.23)

При этом длину дуги захвата можно определить по формуле:

(І5.24)

Когда < 2 скольжение по поверхности почти отсутствует и можно принять = 0,5; тогда:

(15.25)

Коэффициент учитывает влияние внешнего трения и определяется в зависимости от отношения (табл.15.1).

Табл. 15.1 – Формулы для определения коэффициента напряженного состояния

Вид прокатки	Коэффициент напряженного состояния при значении
	1-2	2-4	> 4
Горячая
Холодная

Коэффициент находится по формуле. Коэффициентучитывает влияние внешних недеформированных зон и может быть определен по рекомендациям А.И. Целикова и В.В. Смирнова в интервале 0,5 < < 1 по формуле:

(15.26)

Пушкаревым В.Д. на основе экспериментальных опытов предложены такие формулы для определения :

При (15.27)

При (15.28)

Для случая двухмерной равномерной по толщине деформации (при >1) .

Коэффициент учитывает влияние натяжения. Приблизительно значение может быть найдено по формуле:

, (15.29)

где – давление без учета натяжения.

Согласно данным У. Хесенберга и Р. Симса контактное давление метала на валки р_с с учетом влияния натяжения можно определить так:

, (15.30)

где (15.31)

15.7. Определение сопротивления деформации при горячей прокатке

Согласно с А. Надаи сопротивление деформации описывается уравнением:

(15.32)

Составляющие этого уравнения учитывают влияние на сопротивление деформации температуры, упрочнения, разупрочнения во времени, изменение напряжений в зависимости от скорости деформации с учетом вязкости металла.

До настоящего времени закономерности, которые необходимы для решения уравнения, недостаточно изучены, поэтому на практике для определения σ используют экспериментальные данные в виде конкретных дискретных значений для определенных условий прокатки, или зависимости, которые аппроксимируют экспериментальные данные.

При этом необходимо различать холодную и горячую прокатку. Согласно классической теории обработки металлов давлением, разница между холодной и горячей деформацией заключается в том, что в первом случае рекристаллизация не происходит и возникает существенное деформационное упрочнение; во втором случае деформация происходит при температуре, выше температуры рекристаллизации и упрочнение металла не наблюдается. Однако в последнее время установлено, что такое разделение недостаточно точное. Рекристаллизация происходит во времени и при высокой скорости горячей прокатки не успевает произойти полностью. Это явление в наибольшей степени сказывается при высокой скорости прокатки, что имеет место в чистовых клетях широкополосных станов горячей прокатки.

За реальную характеристику металлов и сплавов может быть принято сопротивление деформации при линейном напряженном состоянии, которое определяется экспериментально испытанием на растяжение или сжатие при термомеханических параметрах, которые совпадают с реальными процессами обработки металлов давлением.

Испытание для определения сопротивления деформации стали и сплавов осуществляют с применением специальных машин, наибольшее распространение среди которых нашли пластометры разных типов. При испытаниях на них можно воспроизвести закон деформации во времени, изменить степень и скорость деформации, проводить испытания при высоких температурах, замерять усилия и деформации в функции времени с помощью тензометрической аппаратуры.

В зависимости от представления результатов испытаний различают разные методы. Рассмотрим некоторые из них.

В графическом методе σ представляют в виде графика с обозначением на линиях температуры и степени деформации.

Иногда σ представляют в виде кривых упрочнения с обозначением на линиях скорости деформации для фиксированных значений температур.

При использовании метода термомеханических коэффициентов значение сопротивления деформации при разных температурах, скорости и степени деформации В.И. Зюзин предлагает определять по зависимости

(15.33)

Среднее или, базисное сопротивление деформации вдинамической зоне деформации определяется при таких параметрах:

t = 1000°С ε = 0,1 и

Метод термомеханических коэффициентов дает возможность расчленить многозначную функциональную зависимость σ () на ряд зависимостей между тремя переменными ,і. Для приведенных ниже сталей и сплавов зависимость сопротивления деформации от температуры выраженной коэффициентом ,может быть представлена в экспоненциальной фор-ме:

, (15.34)

а зависимости коэффициентов и от степени и скорости деформации в степенной форме:

; (15.35, 15.36)

где – постоянные коэффициенты, которые зависят от материала.

Тогда уравнение:

(15.37)

может быть представлено в виде:

(15.38)

Значения коэффициентов уравнения приведены в таблице 15.2.

Таблица 15.2 – Значение постоянных коэффициентов для определения сопротивления деформации

Сталь	, МПа
45	1330	0,0025	0,252	0,143
12ХНЗА	2300	0,0029	0,252	0,143
40Х13	4300	0,0033	0,28	0,087
14Х17Н2	7050	0,0037	0,28	0,087
12Х18Н9Т	3250	0,0028	0,28	0,087
ХН78Т	8900	0,0038	0,28	0,087
ХН75МБТЮ	11000	0,0032	0,35	0,098
ХН10Ю	13300	0,0033	0,35	0,098
ХН50МКВЮ	15000	0,0032	0,35	0,098

Недостатком этого метода является узкий круг исследованных марок сталей.

Большой объем опытов по определению сопротивления деформации металла проведен в НИИМ (Челябинск) под руководством Л.В. Андреюка.

Для определения истинного сопротивления деформации предложена зависимость

(15.39)

где u – скорость деформации, с^-1;

–степень деформации, %;

–температура, ^оС;

–базовое сопротивление деформации, полученное при u = 1с^-1,

ε = 10 % , t = 1000 ^оС

s, а, b, с – постоянные величины, определенные для каждой марки стали (табл.15.3)

При использовании этой формулы нужно учитывать средние по дуге зах-вата значения скорости и степени деформации согласно формул:

А.И. Целикова (15.40)

Е.К. Ларке (15.41)

где n – число оборотов валков, об/мин;

–абсолютное обжатие, мм;

–начальная толщина, мм;

–протяженность дуги захвата.

Таблица 15.3 – Значение постоянных параметров для определения сопротивления деформации по Л.В. Андреюку

Марка стали, сплава		, МПа	а	в	-с
Ст. 3кп	0,885	76,3	0,135	0,164	2,80
Ст. 3сп	0,960	88,8	0,124	0,167	2,54
Ст. 5сп	0,917	87,7	0,144	0,208	3,35
15Г	0,842	100,9	0,126	0,108	2,74
23Г2А	0,962	86,4	0,123	0,229	3,23
35ГС	0,975	87,8	0,136	0,187	2,79
А35Г2	0,940	81,8	0,151	0,122	3,66
30ХГСА	0,966	90,6	0,134	0,250	3,34
15ХСНД	0,880	91,3	0,182	0,226	2,9
20Г2С	1,011	93,8	0,125	0,213	3,65
30ХГСНА	1,051	96,6	0,116	0,140	3,42
15ХГНТА	0,932	105,8	0,108	0,257	3,25
45	1,00	85,7	0,143	0,173	3,05
40Х	0,979	85,8	0,130	0,170	3,62
40ХН	0,935	86,7	0,134	0,234	3,47
10	0,934	87,6	0,125	0,225	2,46
40ХГМ	0,870	100,9	0,173	0,144	2,64
38ХМЮА	1,016	98,0	0,114	0,273	3,72
65Г	1,007	71,2	0,166	0,222	3,02

Продолжение таблицы 15.3

Марка стали, сплава		, МПа	а	в	-с
У7А	0,948	77,1	0,159	0,197	2,87
У10А	0,995	78,9	0,163	0,193	3,57
У12А	1,057	68,6	0,173	0,18	3,26
60С2	0,921	102,9	0,153	0,197	3,46
60С2ХА	0,946	99,0	0,139	0,115	3,84
33А	0,935	47,1	0,198	0,074	3,85
ШХ15	1,01	78,0	0,137	0,220	4,07
12Х2Н4А	0,966	102,0	0,100	0,226	3,20
18Х2Н4ВА	0,971	104,9	0,117	0,165	2,73
ЭП182	0,927	152,9	0,120	0,108	4,63
В2Ф	0,950	121,6	0,135	0,119	3,69
ЭП257	0,947	146,0	0,127	0,103	3,99
30Х5МВНФСА	0,836	182,2	0,124	0,150	4,61
ЭИ962	0,949	157,8	0,101	0,159	3,70
ЗХ2В8Ф	0,895	158,8	0,113	0,113	3,54
40ХНМА	0,966	90,9	0,125	0,175	3,4
Р18	0,780	232,2	0,136	0,100	3,01
1Х13	0,950	142,1	0,102	0,125	3,50
2Х13	0,900	132,2	0,132	0,210	3,26
ВНС14	0,900	134,2	0,124	0,208	4,88
Х17Н2	0,866	123,4	0,130	0,063	4,72
ЭП56	1,23	145,0	0,106	0,136	3,95
ВНС16	0,921	143,0	0,107	0,150	4,93
ЭИ636	0,934	55,4	0,172	0,067	3,64
ЭИ439	1,028	57,3	0,124	0,052	3,70
ЭИ811	0,900	147,0	0,077	0,067	3,23
ЭИ302	0,804	194,0	0,104	0,070	3,00
Х18Н10Т	0,825	217,6	0,112	0,088	4,35
ЭИ654	0,930	186,2	0,155	0,064	4,48
ЭИ448	0,906	213,7	0,072	0,173	2,31
ЭИ432	0,850	212,7	0,122	0,046	3,75
ЭИ319	0,888	188,1	0,093	0,127	3,18
00Х21Н16АГ8	0,887	206,8	0,103	0,128	3,27
Х23Н18	0,848	206,8	0,093	0,105	3,18

Продолжение таблицы 15.3

Марка стали, сплава		, МПа	а	в	-с
000Х21Н21МНБ	0,883	234,2	0,096	0,151	3,21
ЭИ723	0,975	135,2	0,108	0,107	3,94
ЭИ711	1,015	146,0	0,099	0,142	3,12
СП33	0,965	117,6	0,114	0,200	2,95
ЭИ772	0,918	219,6	0,166	0,134	5,38
ЭИ943	0,918	243,0	0,109	0,089	3,46
ЭИ4376	0,885	283,2	0,158	0,037	4,32
ЭИ602	0,809	378,2	0,116	0,153	3,22
ЭИ617	0,753	382,2	0,108	0,118	3,87
ЭП487	0,839	481,1	0,132	0,060	5,47
ЭП109	0,515	753,1	0,124	0,055	6,32
ЭП220	0,694	662,5	0,086	0,026	8,06

В технической литературе приведено большое количество формул для определения среднего контактного давления при прокатке.

(15.42) (15.43)

Формула Экелунда: МПа, (15.42)

где , (15.43)

, (15.44)

, (15.45)

; (15.46)

где η – коэффициент вязкости металла;

Сv – коэффициент, который зависит от скорости прокатки V:

м/с 6 10 15 20

Сv 1 0,8 0,65 0,6

–скорость деформации, с^-1;

–содержание углерода, марганца и хрома в стали.

Формула Гелеи:

МПа (15.47)

где – сопротивление линейной деформации;

–для малолегированных углеродистых сталей;

– для высокоуглеродистых сталей, которые содержат Мn и Сr.

V – угловая скорость, м/с;

с – коэффициент, который зависит от (рис. 57)

Рис. 57 – Значение коэффициента С в зависимости от .

Формула А.Ф. Головина и В.А. Тягунова

, (15.48)

где

– предел прочности стали в холодном отожженном состоянии;

t – температура металла;

при , (15.49)

при , (15.50)

– температура плавления металла.