
- •Методические указания
- •Методические указания
- •Часть 1. Элементы линейной алгебры
- •§ 1. Определители и их скойства
- •§ 2. Матрицы и действия над ними
- •Сложение матриц. Действия над ними
- •§ 3. Системы линейных уравнений
- •Часть 2. Векторная алгебра
- •§ 1. Векторы и линейные операции над ними
- •§ 2. Декартовые прямоугольные координаты в пространстве. Разложение вектора по ортам
- •§ 3. Скалярное произведение векторов
- •§ 4. Векторное произведение векторов
- •§ 5. Смешаноё произведение трёх векторов
- •Часть 3. Аналитическая геаметрия на плоскости и в пространстве
- •§ 1. Предмет аналитической геометрии. Простейшие задачи. Преобразование координат
- •§ 2. Прямая линия на плоскости
- •2.1. Общее уравнение прямой
- •2.2. Уравнение прямой с угловым коэффициентом
- •§ 3. Кривые второго порядка
- •§ 4. Плоскость
- •§ 5. Прямая в пространстве
- •Список использованной литературы
- •Методические указания
- •Методические указания
§ 2. Декартовые прямоугольные координаты в пространстве. Разложение вектора по ортам
Литература: (1, с. 34-42; 2, с. 58-58; 3, с. 222-231)
Координаты точек
Декартова
прямоугольная система координат в
пространстве определяется заданием
единицы масштаба для измерения длин и
трёх пересекающихся в точке
![]() перпендикулярных осей:
перпендикулярных осей:![]() - ось абсцисс, ось
- ось абсцисс, ось![]() - ось ординат и
- ось ординат и![]() - ось аппликат. Если в пространстве
задана точка, то, проектируя её на
соответствующие оси, получим три
координаты точки в пространстве.
- ось аппликат. Если в пространстве
задана точка, то, проектируя её на
соответствующие оси, получим три
координаты точки в пространстве.
Координаты векторов
Положение
координатных осей можно задать с помощью
единичных векторов
![]() ,
,![]() ,
,![]() ,
направленных соответственно по осям
,
направленных соответственно по осям![]() .
Векторы
.
Векторы![]() ,
,![]() ,
,![]() называются основными или базисными
ортами.
называются основными или базисными
ортами.
Пусть задан в
пространстве вектор
![]() своими проекциями на координатные оси:
своими проекциями на координатные оси:![]() ,
,![]() ,
,![]() .
.
Тогда имеет место формула:
![]() (3)
(3)
Формула (3) называется разложением вектора по основным ортам.
Проекции
![]() ,
,![]() ,
,![]() вектора
вектора![]() на координатные оси называются его
координатами. Зная координаты вектора,
можно записать разложение вектора по
основным ортам и, наоборот, зная разложение
вектора по основным ортам, определяют
координаты вектора (коэффициенты при
ортах – есть координаты вектора).
на координатные оси называются его
координатами. Зная координаты вектора,
можно записать разложение вектора по
основным ортам и, наоборот, зная разложение
вектора по основным ортам, определяют
координаты вектора (коэффициенты при
ортах – есть координаты вектора).
Действия над векторами, заданными координатами
Равные вектора имеют равные координаты.
Вектор
![]() ,
направленный из начала координат в
точку
,
направленный из начала координат в
точку![]() ,
называется радиусом – вектором точки
,
называется радиусом – вектором точки![]() .
Проекции радиуса-вектора равны координаты
точки М, т.е.
.
Проекции радиуса-вектора равны координаты
точки М, т.е.
![]() (4)
(4)
Если даны координаты
точек
![]() и
и![]() ,
то координаты вектора
,
то координаты вектора![]() получаются вычитанием из координат его
конца В координат начала А:
получаются вычитанием из координат его
конца В координат начала А:
![]() (5)
(5)
При сложении
(вычитании) векторов их координаты
складываются (вычитаются); при умножении
вектора на число все го координаты
умножаются на это число, т.е. если
![]() ,
,![]() ,
то
,
то
![]() (6)
(6)
![]() (7)
(7)
Если векторы
![]() и
и![]() коллинеарные, то
коллинеарные, то![]() и, следовательно,
и, следовательно,
![]() (8)
(8)
Формула (8) выражает условие коллинеарности двух векторов: для того, чтобы два вектора были коллинеарны, необходимо и достаточно, чтобы их проекции были пропорциональны.
Длинна вектора и его направляющие косинусы
Длина вектора
![]() вычисляется по формуле:
вычисляется по формуле:
![]() (9)
(9)
Если же вектор
![]() задан координатами своих концов А и В,
то длина его вычисляется по формуле:
задан координатами своих концов А и В,
то длина его вычисляется по формуле:
![]() (10)
(10)
С помощью формулы (10) находится расстояние между двумя точками А и В.
Направление вектора
в пространстве определяется углами
![]() ,
которые вектор составляет с осями
координат:
,
которые вектор составляет с осями
координат:![]() ,
,![]() ,
,![]() .
Косинусы этих углов называются
направляющими косинусами.
.
Косинусы этих углов называются
направляющими косинусами.
![]() ,
,
![]() ,
,![]() (11)
(11)
Направляющие
косинусы являются координатами орта
вектора
![]() ,
,
![]() (12)
(12)
Направляющие косинусы связаны между собой соотношением:
![]()
Примеры
1) Определить, при
каких значениях
![]() и
и![]() векторы
векторы![]() и
и![]() коллинеарны.
коллинеарны.
Решение. Из формулы
разложения вектора по ортам (3) определим
координаты данных векторов:
![]() ;
;![]() .
Из условия коллинеарности векторов (8)
получим:
.
Из условия коллинеарности векторов (8)
получим:
![]() .
.
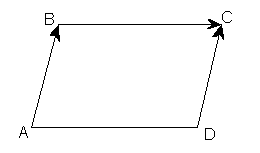
2) Даны три
последовательные вершины параллелограмма
![]() ,
,![]() ,
,![]() .
Найти четвёртую вершину
.
Найти четвёртую вершину![]() ,
противоположную вершине В.
,
противоположную вершине В.
Решение. Так как
![]() - параллелограмм, то
- параллелограмм, то![]()
![]()
![]()
Из равенства
векторов получим :
![]() ;
;![]() ;
;![]() .
Следовательно,
.
Следовательно,![]()
3) Найти длину и
направляющие косинусы вектора
![]() ,
где
,
где![]() и
и![]() .
.
Решение. Используя формулу (10), имеем:
![]()
![]()
Тогда по формулам (11):
![]() ,
,
![]() ,
,![]() .
.
4) Даны векторы
![]() и
и![]() .
Найти координаты вектора
.
Найти координаты вектора![]() .
.
Решение. По формуле (7) найдём:
![]()
![]()
Тогда по формуле (6):
![]()
Вопросы для самопроверки
Как задаётся прямоугольная декартова система координат?
Что такоё основные орты?
Запишите формулу разложения вектора по ортам. Как определяются координаты и компоненты вектора?
Что называется направляющими косинусами вектора и как они определяются?
Как проводятся линейные операции над векторами, заданными своими координатами?
При каких условиях векторы коллинеарны?
Как находится орт
вектора
![]() ,
заданного своими координатами?
,
заданного своими координатами?
Задания для самостоятельного решения
Найти орт вектора
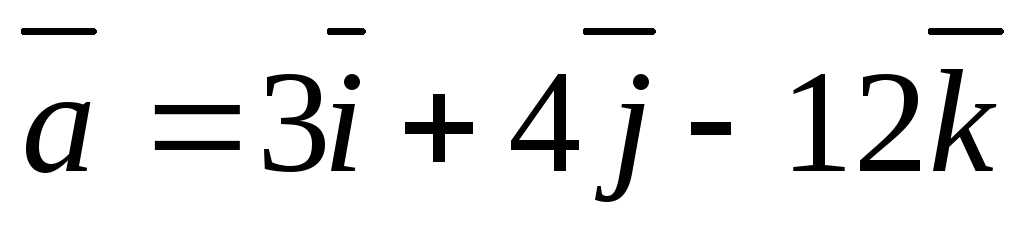 .
.Найти длину и направляющие косинусы вектора
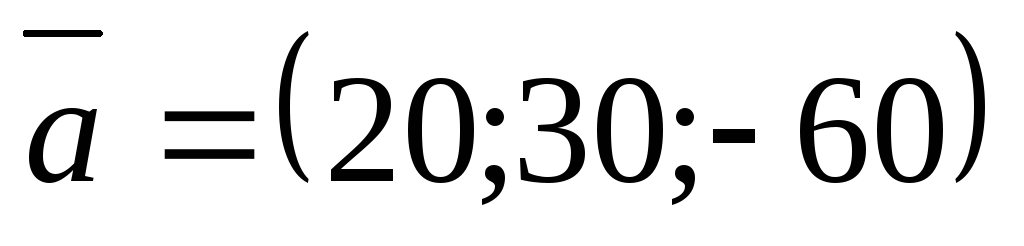
Найти вектор
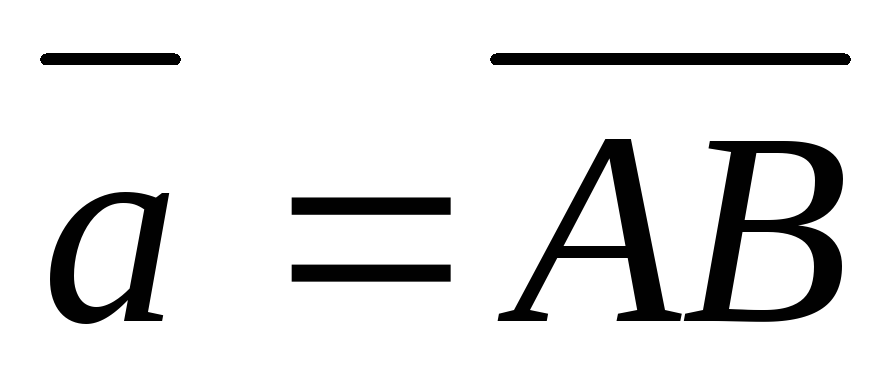 ,
если
,
если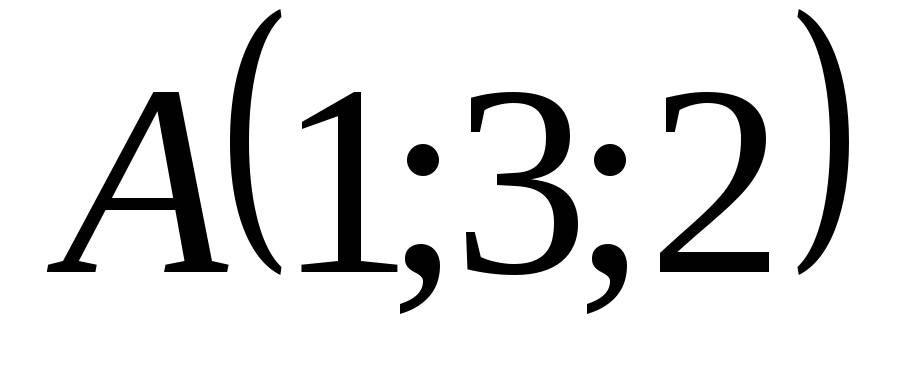 и
и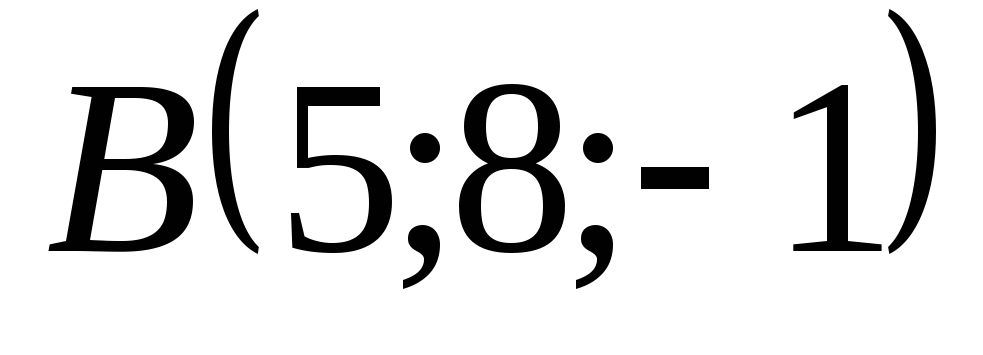 .
.Даны два вектора
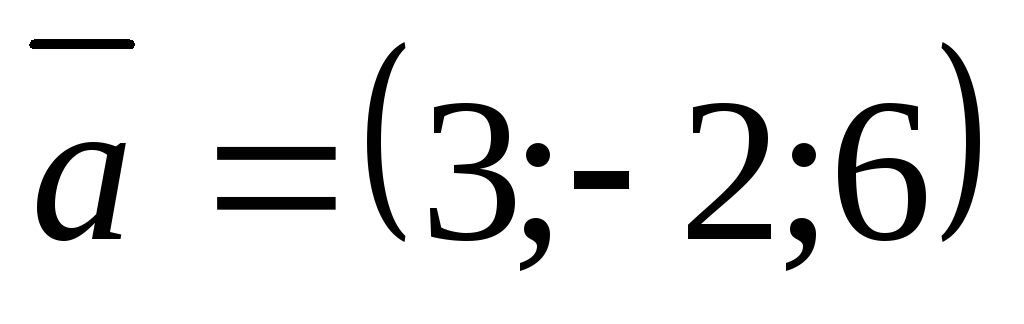 и
и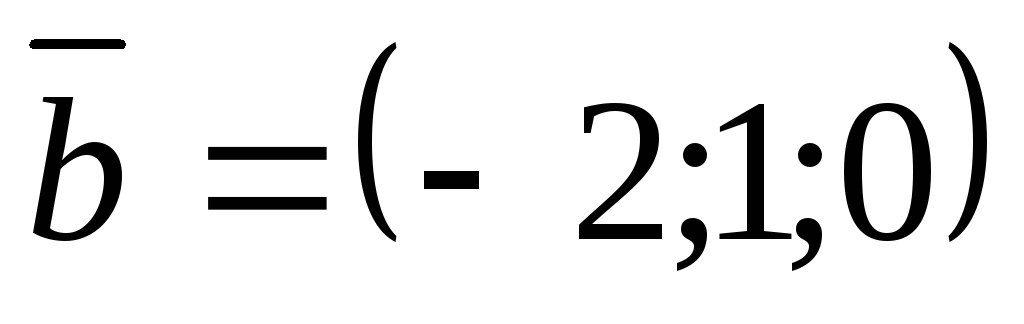 .
Определить проекцию вектора
.
Определить проекцию вектора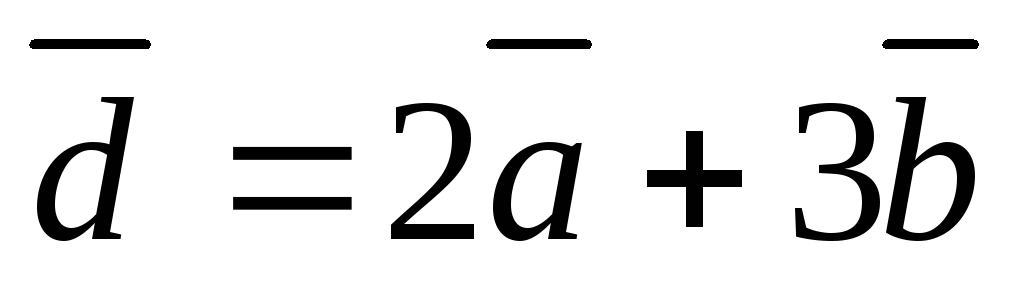 .
.Определить, при каких значениях
 и
и векторы
векторы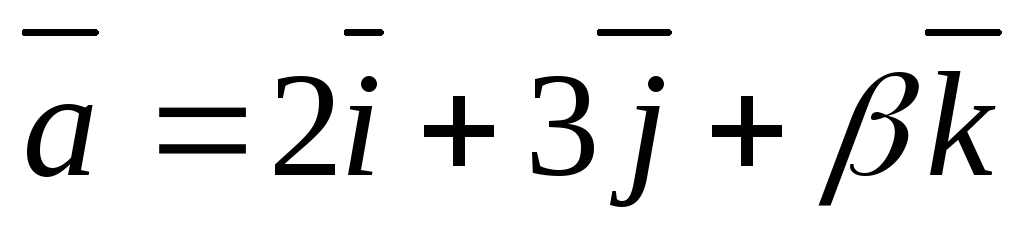 и
и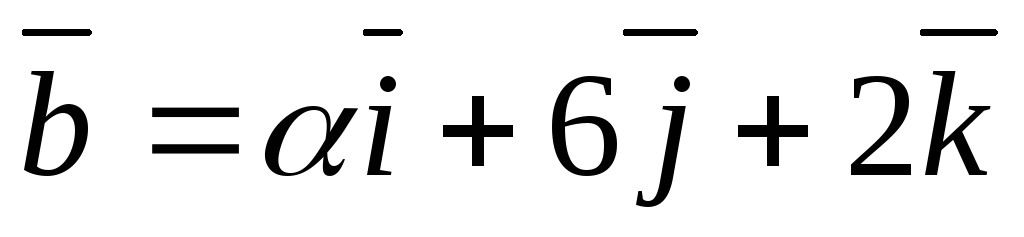 коллинеарны.
коллинеарны.Векторы
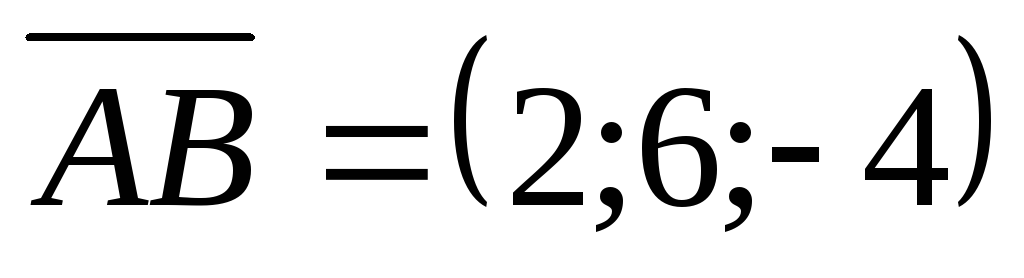 и
и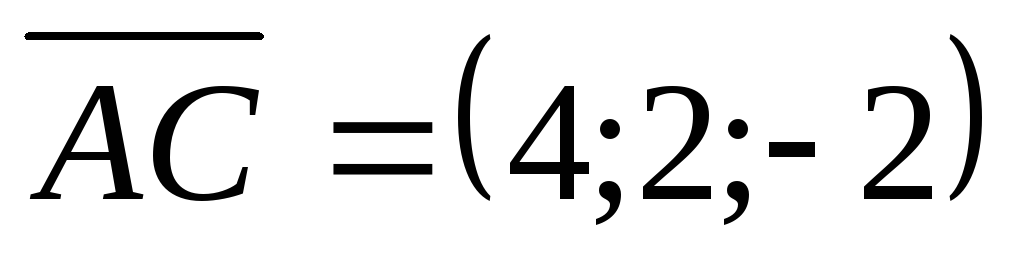 совпадают со сторонами треугольника
АВС. Определить координаты векторов,
приложенных к вершинам треугольника
и совпадающих с его медианами АМ,
совпадают со сторонами треугольника
АВС. Определить координаты векторов,
приложенных к вершинам треугольника
и совпадающих с его медианами АМ,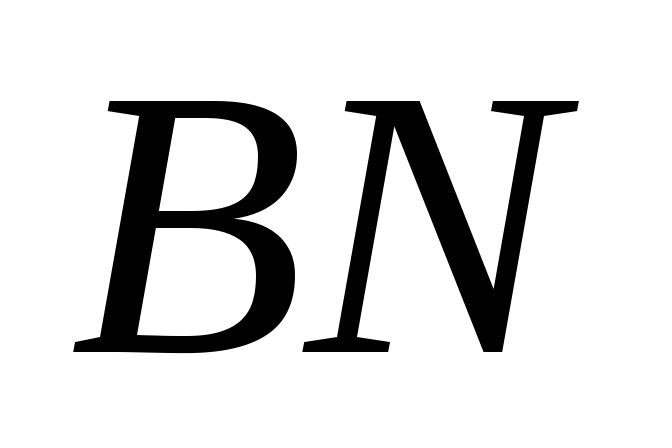 ,
СР.
,
СР.Даны три вектора
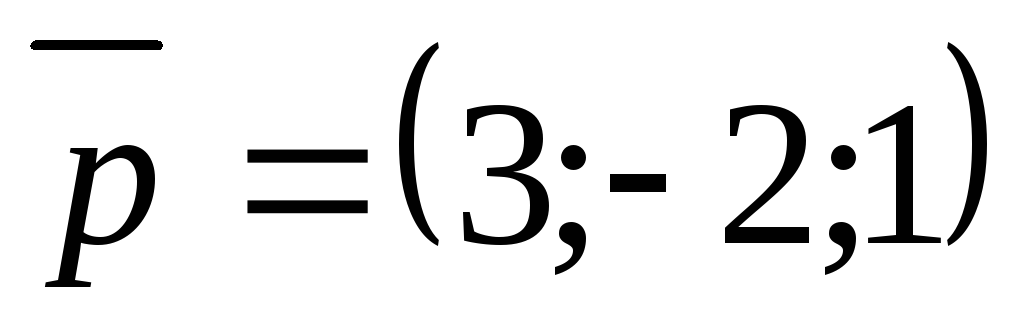 ,
,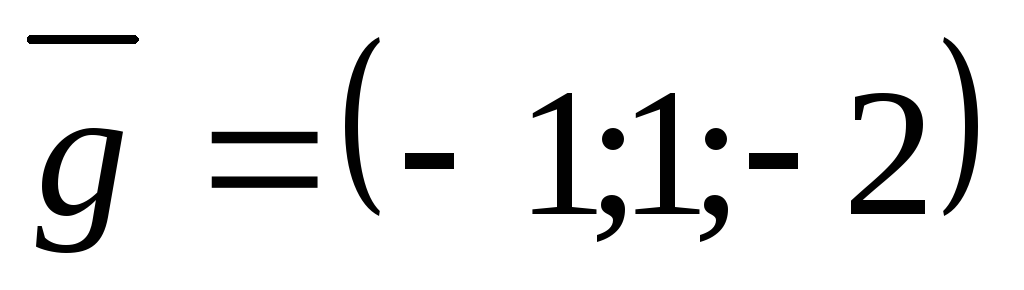 и
и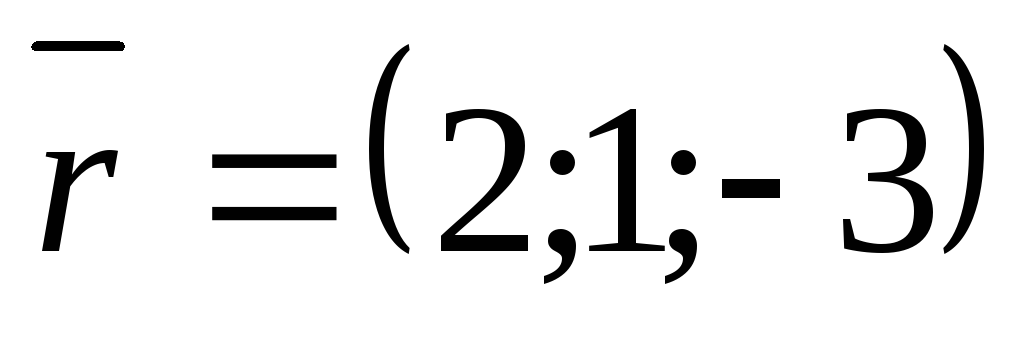 .
Найти разложение вектора
.
Найти разложение вектора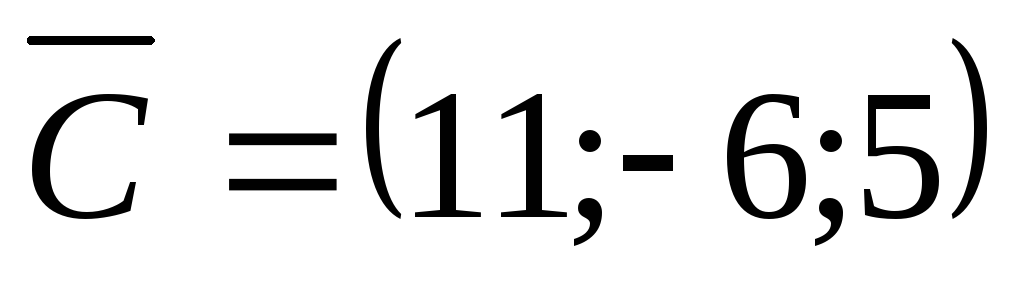 по базису
по базису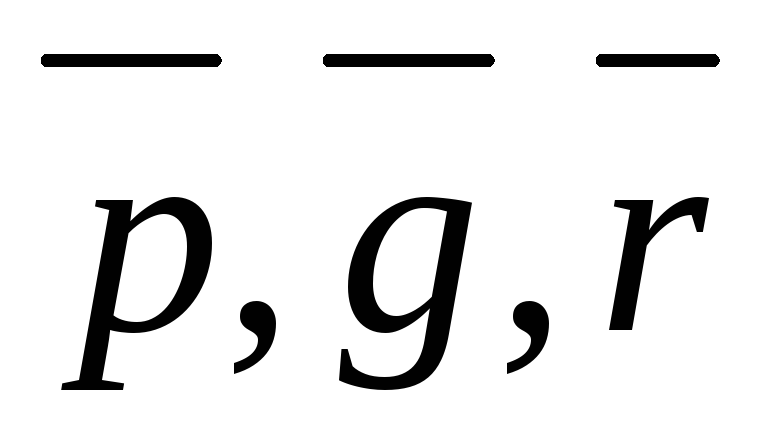 .
.
Ответы к примерам
2.7.1.
![]() 2.7.2.
2.7.2.![]()
2.7.3.
![]() 2.7.4.
2.7.4.![]()
2.7.5.
![]() 2.7.6.
2.7.6.![]()
2.7.7.
![]()
