
- •Методические указания
- •Методические указания
- •Часть 1. Элементы линейной алгебры
- •§ 1. Определители и их скойства
- •§ 2. Матрицы и действия над ними
- •Сложение матриц. Действия над ними
- •§ 3. Системы линейных уравнений
- •Часть 2. Векторная алгебра
- •§ 1. Векторы и линейные операции над ними
- •§ 2. Декартовые прямоугольные координаты в пространстве. Разложение вектора по ортам
- •§ 3. Скалярное произведение векторов
- •§ 4. Векторное произведение векторов
- •§ 5. Смешаноё произведение трёх векторов
- •Часть 3. Аналитическая геаметрия на плоскости и в пространстве
- •§ 1. Предмет аналитической геометрии. Простейшие задачи. Преобразование координат
- •§ 2. Прямая линия на плоскости
- •2.1. Общее уравнение прямой
- •2.2. Уравнение прямой с угловым коэффициентом
- •§ 3. Кривые второго порядка
- •§ 4. Плоскость
- •§ 5. Прямая в пространстве
- •Список использованной литературы
- •Методические указания
- •Методические указания
Список использованной литературы
Бугров Я.С., Никольский С.М. Элементы линейной алгебры и аналитической геометрии. – М.:Наука 1980. – 176 с.
Шнейдер В.Е., Слуцкий А.И.,Шумов А.С. Краткий курс высшей математики. – М: Высш. шк., 1978. – Т.1. – 384 с.
Щипачёв В.С. Высшая математика. – М.: Высш. шк., 1985. – 472 с.
Долгов Н.М. Высшая математика. Киев: Вища шк., 1988. – 416 с.
МЕТОДИЧЕСКИЕ УКАЗАНИЯ
К САМОСТОЯТЕЛЬНОМУ ИЗУЧЕНИЮ ТЕМЫ
«ВЕКТОРНАЯ И ЛИНЕЙНАЯ АЛГЕБРА. ПИЛОЖЕНИЯ К ЗАДАЧАМ АНАЛИТИЧЕСКОЙ ГЕОМЕТРИИ» по курсу «Высшая математика»
(для студентов всех специальностей)
Составитель ШМАНЁВА Лина Васильевна
Редактор Л.Н. Полчанникава
Корректор Е.Р. Иванова
Тех. Редактор С.Х. Аниськова
Пл. изд. № 18 1989 г.
Подп. В печать
24.02.89. Формат 60![]() 84
84![]() .
Бумага тип. № 2. Офсетная печать. Усл.
Печ. Л. 4,65. Усл. Кр.-отт. 4,77. Уч.-изд. Л. 4,72.
Тираж 1050 экз. Зак. 9-2191.
.
Бумага тип. № 2. Офсетная печать. Усл.
Печ. Л. 4,65. Усл. Кр.-отт. 4,77. Уч.-изд. Л. 4,72.
Тираж 1050 экз. Зак. 9-2191.
Бесплатно.
КГМИ, 349104, Коммунарск, пр. Ленина, 16
ДМАПП, 340050, Донецк, ул. Артёма, 69
Бесплатно.
Зак. 9-2191
Министерство высшего и среднего специального образования УССР
КОММУНАРСКИЙ ГОРНО-МЕТАЛУРГИЧЕСКИЙ ИНСТИТУТ
Методические указания
К самостоятельному изучению темы «ВЕКТОРНАЯ И ЛИНЕЙНАЯ АЛГЕБРА»
Коммунарск КГМИ 1991
Министерство высшего и среднего специального образования УССР
КОММУНАРСКИЙ ГОРНО-МЕТАЛУРГИЧЕСКИЙ ИНСТИТУТ
Методические указания
К самостоятельному изучению темы «ВЕКТОРНАЯ И ЛИНЕЙНАЯ АЛГЕБРА»
(для студентов всех специальностей)
Утверждено
На заседании кафедры
Высшей математики
Протокол № 1 от 31.08.90
Коммунарск КГМИ 1991
УДК 512.94 : 517.94
Методические указания к самостоятельному изучению темы «Векторная и линейная алгебра» (для студентов всех специальностей) / Сост. Л.В. Шманёва. – Коммунарск: КГМИ, 1991. – 16 с.
Предлагаемая работа является продолжением ранее изданных методических указаний № 757 (изданных в 1989 году) и содержит индивидуальные задания для каждого студента по основным разделам векторной и линейной алгебры, а также аналитической геометрии.
Составитель Л.В. Шманёва, ст. преп.
Рецензисты: Г.М. Финкельштейн, доц.
Е.Я. Косюга, ст. преп.
Задание 1
Решить систему с помощью определителей и проверить решение методом Гаусса.
1)
 2)
2) 3)
3)
4)
 5)
5) 6)
6)
7)
 8)
8) 9)
9)
10)
 11)
11) 12)
12)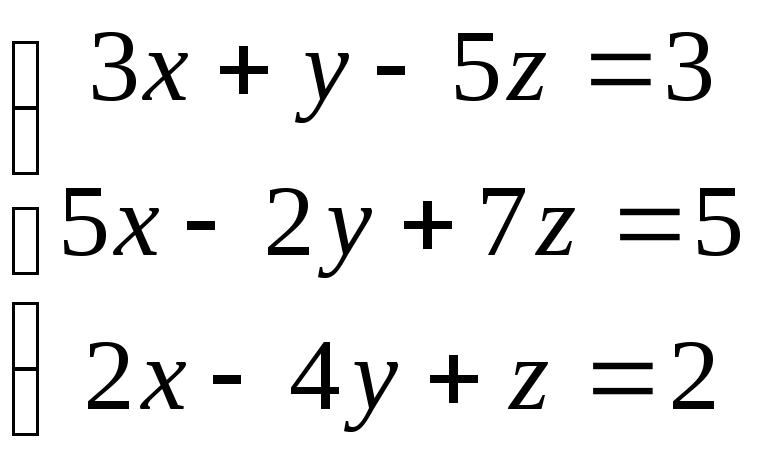
13)
 14)
14) 15)
15)
16)
 17)
17) 18)
18)
19)
 20)
20) 21)
21)
22)
 23)
23) 24)
24)
25)
 26)
26) 27)
27)
28)
 29)
29)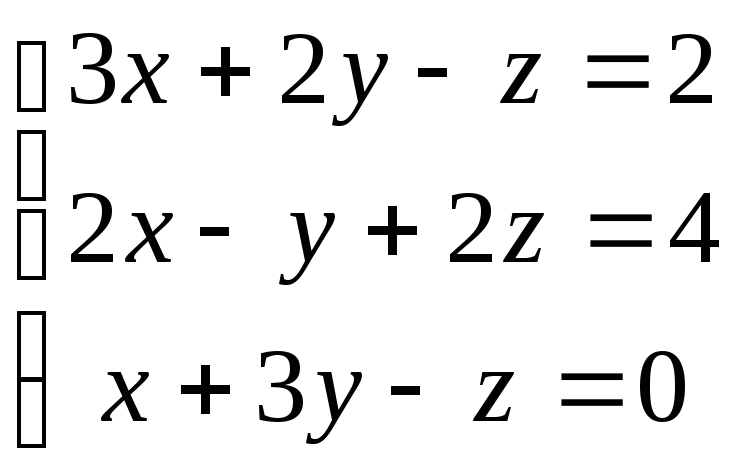 30)
30)
Задание 2
Даны три силы
![]() ,
,![]() ,
,![]() ,
приложенные к одной точке. Вычислить
работу равнодействующей силы, когда её
точка приложения перемещается из точки
,
приложенные к одной точке. Вычислить
работу равнодействующей силы, когда её
точка приложения перемещается из точки![]() в точку
в точку![]() .
.
|
Вариант |
|
|
|
|
|
|
1 |
2, -1, 3 |
1, 2, 0 |
-1, 0, 0 |
1, 1, 1 |
2, 1, 1 |
|
2 |
1, 2, 0 |
-1, 0, -1 |
2, 1, 1 |
1, 2, 3 |
1, 1, 1 |
|
3 |
-1, 1, 1 |
2, 1, 1 |
1, 2, 2 |
1, 0, 0 |
2, 1, -1 |
|
4 |
1, 0, 1 |
1, -2, 2 |
-1, 2, 1 |
2, -1, 0 |
2, 0, 1 |
|
5 |
-1, 2, 1 |
0, 0, -1 |
0, 1, 1 |
3, -1, 2 |
1, 2, 1 |
|
6 |
0, 1, 1 |
1, 2, -2 |
2, 1, 3 |
4, 2, -1 |
2, 1, 1 |
|
7 |
1, -1, 1 |
0, -1, 1 |
1, 2, 1 |
3, 1, 2 |
2, 1, 0 |
|
8 |
2, 1, 3 |
1, 2, -1 |
0, -1, 2 |
1, -1, 0 |
0, 1, 2 |
|
9 |
2, -1, 3 |
2, 1, -3 |
-1, 2, 1 |
2, 0, 1 |
4, 2, 1 |
|
10 |
1, -1, 3 |
-2, 0, -1 |
1, 2, 0 |
0, 2, 1 |
3, 1, 1 |
|
11 |
1, 0, 2 |
-2, 0, 1 |
2, 1, 1 |
0, 0, 1 |
1, -1, 0 |
|
12 |
1, 1, 0 |
2, 0, 0 |
1, -1, 2 |
1, -1, 1 |
2, 1, 1 |
|
13 |
-1, 0, 2 |
2, 1, -1 |
1, -1, 1 |
2, 1, 0 |
1, -1, 1 |
|
14 |
1, 1, 1 |
3, 2, -2 |
-2, 1, 0 |
3, 1, -2 |
1, -1, 2 |
|
15 |
2, -1, 0 |
1, -2, 1 |
-1, 0, 2 |
2, -1, 0 |
2, 1, 1 |
|
16 |
1, -1, 2 |
2, 1, -1 |
-2, 1, 1 |
2, 2, 1 |
1, 1, 1 |
|
17 |
2, 0, 2 |
1, -2, 1 |
0, -1, -2 |
3, 1, -1 |
2, 1, 4 |
|
18 |
2, 1, 0 |
1, 3, -1 |
-2, 1, 3 |
2, -1, 1 |
2, 1, 2 |
|
19 |
1, 2, 3 |
2, 1, 1 |
-1, 2, -2 |
4, 1, -1 |
3, 1, 1 |
|
20 |
1, 0, -2 |
1, 2, 0 |
1, -2, 1 |
3, 2, 2 |
2, 2, 3 |
|
21 |
2, -1, 1 |
1, -1, 1 |
-1, 0, 0 |
3, -1, 1 |
2, 3, 1 |
|
22 |
1, 2, -1 |
2, -1, 3 |
1, -2, 0 |
2, -2, 1 |
1, 1, -1 |
|
23 |
3, 1, 2 |
1, 2, -1 |
2, -1, 0 |
1, 1, 2 |
2, 1, 1 |
|
24 |
2, 1, -3 |
1, 2, 2 |
-2, -1, 3 |
1, 0, 2 |
1, 2, 1 |
|
25 |
-2, 0, 1 |
1, 2, 0 |
-1, 2, 0 |
-1, 0, 1 |
2, -1, 1 |
|
26 |
1, 0, -1 |
2, -1, 3 |
3, 1, -2 |
3, 0, -2 |
1, 2, 3 |
|
27 |
0, 2, 3 |
3, 1, 2 |
0, 2, 0 |
2, -1, 3 |
3, 1, 0 |
|
28 |
1, 2, 3 |
-1, 1, 1 |
2, -1, 3 |
3, -2, 1 |
4, 0, 2 |
|
29 |
3, 2, 1 |
1, -1, 2 |
-1, 2, 1 |
2, 0, -2 |
3, 2, -1 |
|
30 |
2, -1, 2 |
0, -2, 3 |
2, 0, -1 |
1, -2, 1 |
2, 2, 1 |
Задание 3
Вычислить площадь
параллелограмма, построенного на
векторах
![]() и
и![]() ,
если известны:
,
если известны:
|
Вариант |
|
|
|
|
|
|
1 |
|
|
1 |
2 |
30˚ |
|
2 |
|
|
2 |
3 |
45˚ |
|
3 |
|
|
3 |
4 |
60˚ |
|
4 |
|
|
4 |
5 |
90˚ |
|
5 |
|
|
5 |
6 |
120˚ |
|
6 |
|
|
6 |
4 |
150˚ |
|
7 |
|
|
2 |
1 |
135˚ |
|
8 |
|
|
7 |
2 |
120˚ |
|
9 |
|
|
5 |
2 |
90˚ |
|
10 |
|
|
8 |
3 |
30˚ |
|
11 |
|
|
6 |
1 |
45˚ |
|
12 |
|
|
5 |
4 |
135˚ |
|
13 |
|
|
4 |
2 |
150˚ |
|
14 |
|
|
2 |
5 |
120˚ |
|
15 |
|
|
1 |
3 |
135˚ |
|
16 |
|
|
3 |
2 |
90˚ |
|
17 |
|
|
2 |
1 |
30˚ |
|
18 |
|
|
3 |
2 |
60˚ |
|
19 |
|
|
8 |
3 |
45˚ |
|
20 |
|
|
9 |
2 |
120˚ |
|
21 |
|
|
4 |
5 |
135˚ |
|
22 |
|
|
2 |
2 |
30˚ |
|
23 |
|
|
3 |
2 |
45˚ |
|
24 |
|
|
4 |
3 |
90˚ |
|
25 |
|
|
3 |
1 |
30˚ |
|
26 |
|
|
2 |
3 |
45˚ |
|
27 |
|
|
3 |
3 |
120˚ |
|
28 |
|
|
2 |
1 |
135˚ |
|
29 |
|
|
3 |
2 |
60˚ |
|
30 |
|
|
2 |
3 |
90˚ |
Задание 4
Даны вершины треугольника АВС. Найти: 1) длину стороны ВС; 2) уравнение ВС; 3) уравнение высоты АМ; 4) длину высоты АМ; 5) площадь треугольника АВС; 6) величину угла В; 7) координаты точки пересечения медиан треугольника.
|
Вариант |
А |
В |
С |
|
1 |
1, 1 |
-3, -2 |
3, -4 |
|
2 |
1, -1 |
-3, 1 |
3, 3 |
|
3 |
1, 2 |
-3, -1 |
0, -2 |
|
4 |
-1, 1 |
-3, -2 |
2, -2 |
|
5 |
-1, 2 |
6, 0 |
0, -2 |
|
6 |
-1, 0 |
3, 4 |
6, -2 |
|
7 |
0, 1 |
4, 3 |
6, -1 |
|
8 |
1, 0 |
-3, -2 |
3, -3 |
|
9 |
0, -1 |
-6, 1 |
-4, -5 |
|
10 |
2, 1 |
-3, 0 |
-1, -5 |
|
11 |
2, -1 |
0, 6 |
-5, 0 |
|
12 |
2, 3 |
-2, 5 |
-6, 0 |
|
13 |
-3, 2 |
2, 3 |
6, -1 |
|
14 |
3, 2 |
-2, 5 |
-1, 5 |
|
15 |
-3, -2 |
0, -5 |
5, 0 |
|
16 |
3, 0 |
-1, -6 |
-3, 1 |
|
17 |
3, 1 |
-1, 4 |
-3, -1 |
|
18 |
3, -1 |
-1, 1 |
0, -4 |
|
19 |
0, 3 |
6, -1 |
-1, -3 |
|
20 |
0, -3 |
4, 6 |
-1, -2 |
|
21 |
-3, 0 |
2, 3 |
6, -1 |
|
22 |
3, 4 |
-1, 1 |
2, -1 |
|
23 |
4, 3 |
6, -1 |
1, 0 |
|
24 |
4, -3 |
1, 1 |
7, 2 |
|
25 |
-3, 4 |
0, -2 |
6, 1 |
|
26 |
1, 0 |
0, 2 |
-1, 1 |
|
27 |
0, 1 |
-2, 0 |
-1, -1 |
|
28 |
2, 1 |
0, 3 |
-1, 2 |
|
29 |
-1, 0 |
2, 2 |
5, -2 |
|
30 |
0, -2 |
5, 2 |
7, -4 |
Задание 5
Даны вершины
пирамиды
![]() .
Найти: угол между рёбрами АВ и
.
Найти: угол между рёбрами АВ и![]() ;
2) площадь грани АВС; 3) проекцию АВ на
;
2) площадь грани АВС; 3) проекцию АВ на![]() ;
4) объём пирамиды
;
4) объём пирамиды![]() ;
5) длину высоты пирамиды
;
5) длину высоты пирамиды![]() ;
6) каноническое уравнение прямой,
проходящей через точку
;
6) каноническое уравнение прямой,
проходящей через точку![]() перпендикулярно плоскости АВС.
перпендикулярно плоскости АВС.
|
Вариант |
А |
В |
С |
|
|
1 |
1, 0, 0 |
0, 2, 1 |
2, 3, 4 |
-2, 1, 3 |
|
2 |
2, 0, 0 |
1, 2, 2 |
-1, 1, 1 |
3, -1, 1 |
|
3 |
3, 0, 0 |
1, 1, 1 |
2, 1, 0 |
-1, 2, 2 |
|
4 |
-1, 0, 0 |
2, 1, 0 |
3, 2, -1 |
1, 1, 1 |
|
5 |
-2, 0, 0 |
2, 1, 0 |
3, -1, 2 |
1, 2, 1 |
|
6 |
-3, 0, 0 |
3, 1, 1 |
2, -1, 2 |
1, 2, -1 |
|
7 |
1, 1, 0 |
2, 0, 1 |
1, 3, 0 |
0, 0, 4 |
|
8 |
1, 2, 0 |
-2, 0, 1 |
0, 3, 4 |
3, 1, 2 |
|
9 |
1, 3, 0 |
3, 1, 2 |
-1, 2, 1 |
-2, 1, -1 |
|
10 |
1, -2, 0 |
2, 1, 1 |
-1, 2, 2 |
0, 0, 3 |
|
11 |
1, -1, 0 |
2, 0, 0 |
0, -2, 1 |
4, 1, 2 |
|
12 |
1, -3, 0 |
3, 0, 1 |
2, 1, 2 |
-1, 2, 3 |
|
13 |
2, 1, 0 |
3, 2, 2 |
1, 0, 1 |
-1, 3, 3 |
|
14 |
2, 2, 0 |
1, 3, 1 |
-1, 1, 2 |
3, -1, 3 |
|
15 |
2, -2, 0 |
-1, 3, 4 |
-1, 4, 2 |
1, -2, 2 |
|
16 |
-2, 1, 0 |
1, -1, 1 |
2, 2, 2 |
3, 0, 3 |
|
17 |
-2, -1, 0 |
1, 1, -1 |
3, 2, 1 |
4, 0, 2 |
|
18 |
2, 0, 1 |
3, 2, 2 |
-1, 1, 0 |
0, -1, 3 |
|
19 |
3, 0, 1 |
4, 2, 2 |
2, -1, 1 |
-2, 2, 0 |
|
20 |
1, 0, 1 |
2, -2, 3 |
0, 1, 2 |
3, 3, 0 |
|
21 |
-2, 0, 1 |
2, 2, 2 |
1, 1, 3 |
-1, 3, -1 |
|
22 |
-2, 0, -1 |
2, -1, 0 |
1, 1, 1 |
3, 4, 2 |
|
23 |
2, 0, 2 |
3, 1, 1 |
1, 2, -1 |
-1, 3, 0 |
|
24 |
3, 0, 2 |
2, 2, 1 |
4, 1, 0 |
-1, 4, 3 |
|
25 |
3, 0, 4 |
1, 1, 3 |
2, -1, -1 |
4, 2, 1 |
|
26 |
2, 0, 4 |
1, 1, 2 |
-1, 2, 0 |
0, -1, 3 |
|
27 |
2, 0, 0 |
0, 0, 0 |
1, -1, 0 |
1, 1, 0 |
|
28 |
0, 0, 1 |
0, 0, -2 |
1, 0, 0 |
0, -1, 1 |
|
29 |
1, 1, -1 |
1, 0, 0 |
0, 1, 0 |
0, 0, 1 |
|
30 |
1, 1, -1 |
1, -1, 0 |
2, 1, -1 |
3, 2, 1 |
Задание 6
Привести к каноническому виду и построить:
1.
![]()
2.
![]()
3.
![]()
4.
![]()
5.
![]()
6.
![]()
7.
![]()
8.
![]()
9.
![]()
10.
![]()
11.
![]()
12.
![]()
13.
![]()
14.
![]()
15.
![]()
16.
![]()
17.
![]()
18.
![]()
19.
![]()
20.
![]()
21.
![]()
22.
![]()
23.
![]()
24.
![]()
25.
![]()
26.
![]()
27.
![]()
28.
![]()
29.
![]()
30.
![]()
Задание 7
Вычертить область
![]() ,
заданную неравенствами:
,
заданную неравенствами:
1.
![]() ;
;![]() ;
;![]()
2.
![]() ;
;![]() ;
;![]()
3.
![]() ;
;![]() ;
;![]()
4.
![]() ;
;![]() ;
;![]()
5.
![]() ;
;![]() ;
;![]()
6.
![]() ;
;![]() ;
;![]()
7.
![]() ;
;![]() ;
;![]()
8.
![]() ;
;![]() ;
;![]()
9.
![]() ;
;![]() ;
;![]()
10.
![]() ;
;![]() ;
;![]()
11.
![]() ;
;![]() ;
;![]()
12.
![]() ;
;![]() ;
;![]()
13.
![]() ;
;![]() ;
;![]()
14.
![]() ;
;![]() ;
;![]()
15.
![]() ;
;![]() ;
;![]()
16.
![]() ;
;![]() ;
;![]()
17.
![]() ;
;![]() ;
;![]()
18.
![]() ;
;![]() ;
;![]()
19.
![]() ;
;![]() ;
;![]()
20.
![]() ;
;![]() ;
;![]()
21.
![]() ;
;![]() ;
;![]()
22.
![]() ;
;![]() ;
;![]()
23.
![]() ;
;![]() ;
;![]()
24.
![]() ;
;![]() ;
;![]()
25.
![]() ;
;![]() ;
;![]()
26.
![]() ;
;![]() ;
;![]()
27.
![]() ;
;![]() ;
;![]()
28.
![]() ;
;![]() ;
;![]()
29.
![]() ;
;![]() ;
;![]()
30.
![]() ;
;![]() ;
;![]()
Распределение заданий по вариантам
Таблица 1
-
Вари
ант
Номер задания
1-я группа
2-я группа
3-я группа
4-я группа
5-я группа
1
2
3
4
5
6
7
1
2
3
4
5
6
7
1
2
3
4
5
6
7
1
2
3
4
5
6
7
1
2
3
4
5
6
7
1
2
3
4
5
6
1
1
20
9
8
10
2
15
10
2
3
30
1
2
25
4
15
30
1
10
26
25
15
26
2
14
3
6
7
5
14
30
15
1
13
20
2
3
22
7
6
20
12
14
12
5
13
29
2
4
30
8
20
28
4
17
27
23
19
21
4
17
5
28
9
10
16
29
14
2
3
21
3
5
30
3
4
30
22
13
14
8
23
28
3
6
20
12
10
26
7
27
28
21
23
16
6
20
7
26
11
15
18
28
13
3
23
22
4
7
29
5
2
11
1
12
16
11
4
27
4
8
15
16
5
24
5
7
29
19
27
11
8
23
9
24
13
20
22
27
12
4
1
23
5
9
27
1
10
21
11
8
18
14
14
26
5
10
5
20
25
22
30
1
24
17
30
6
10
25
11
22
15
25
20
26
11
5
11
24
6
11
25
2
12
1
21
11
20
17
24
25
6
12
10
24
30
20
3
11
25
14
29
1
12
28
13
20
17
30
24
25
10
6
21
25
7
13
23
4
14
12
13
10
21
20
2
24
7
14
1
28
1
18
28
21
20
13
25
27
14
30
15
18
19
1
26
24
9
7
2
26
8
25
7
14
30
22
23
9
22
23
12
23
8
16
6
30
6
16
26
2
21
11
21
22
16
29
17
16
5
6
28
23
8
8
12
27
9
17
19
8
18
2
3
7
24
26
22
21
9
18
11
26
11
14
24
12
22
9
17
17
18
26
19
14
3
11
30
22
7
9
22
28
10
19
17
11
20
13
4
6
26
29
1
22
10
20
16
22
16
12
22
22
23
8
13
12
20
24
21
12
1
16
12
21
6
10
4
29
11
21
15
13
19
23
14
5
28
30
11
20
11
22
21
18
21
10
20
3
15
7
9
7
22
21
23
10
2
21
10
20
5
30
14
30
12
23
13
15
17
3
24
4
30
28
21
19
12
24
26
14
26
8
18
13
16
6
5
2
24
19
25
8
4
26
8
19
4
29
24
10
13
15
11
17
15
14
5
3
29
25
5
18
13
26
29
10
2
6
16
23
17
5
1
28
26
16
27
4
6
2
6
18
3
28
5
11
14
27
9
19
13
24
15
27
22
15
17
14
28
24
6
7
4
14
4
18
4
2
2
23
28
13
29
2
8
7
4
17
2
27
15
12
15
29
21
10
11
4
25
1
25
19
25
16
15
30
19
2
12
2
12
14
19
1
6
18
30
10
28
1
12
12
2
16
1
26
25
13
16
2
5
12
9
15
6
16
23
16
6
15
16
29
14
3
17
1
10
24
10
2
10
13
1
7
30
3
10
17
1
15
16
25
6
14
17
4
3
6
7
25
16
17
19
13
16
14
17
27
9
7
22
3
8
5
11
3
14
8
3
4
26
5
16
22
3
14
17
24
16
15
18
6
1
16
5
5
26
18
17
10
26
13
18
25
4
11
27
5
4
15
12
10
18
3
5
1
24
7
14
27
5
13
18
23
26
16
19
8
2
18
3
16
7
19
15
7
17
12
19
23
3
15
3
7
2
25
13
12
22
4
7
3
22
9
18
3
7
12
19
22
7
17
20
10
4
20
1
26
17
21
13
4
7
11
20
21
8
19
8
9
29
6
14
15
26
9
9
5
20
11
22
8
9
11
20
21
27
18
21
12
6
22
16
6
27
20
11
1
27
10
21
19
13
23
13
11
27
16
5
16
3
29
11
2
18
13
20
13
11
10
21
20
17
19
22
14
8
24
29
17
8
22
9
3
8
9
22
17
18
27
18
13
25
26
6
18
7
24
13
8
16
15
24
18
13
9
22
19
8
1
23
16
10
26
28
27
18
23
8
6
18
8
23
15
23
29
23
15
23
8
7
20
11
19
15
11
14
30
26
23
15
8
23
18
28
2
24
18
12
28
27
7
28
24
7
9
28
7
24
13
28
25
28
17
19
18
8
22
16
14
17
6
12
29
28
28
17
7
24
17
18
3
25
20
14
30
26
18
9
6
12
9
6
25
11
2
21
4
19
21
28
9
24
25
30
19
9
10
27
20
3
4
19
6
25
16
9
4
26
22
16
29
25
28
19
26
5
15
19
5
26
9
7
17
9
21
17
9
1
30
24
25
21
12
8
25
5
9
21
5
26
15
19
5
27
24
18
27
24
8
29
28
4
18
29
1
27
7
12
13
14
23
15
19
2
29
28
20
23
15
6
23
21
14
23
4
27
14
29
6
28
26
24
25
23
19
10
27
3
21
10
2
28
1
17
9
19
25
13
29
3
28
4
5
25
18
4
21
23
19
25
3
28
13
10
7
29
28
26
23
21
29
20
30
2
24
20
3
29
5
22
5
24
27
11
20
4
27
8
10
27
22
2
19
25
24
29
2
29
12
30
8
30
30
28
21
22
9
30
29
1
27
30
4
30
3
27
1
29
29
9
30
30
26
12
15
29
27
1
17
27
29
27
1
30
11
20
9
Указание.
Предлагается для самостоятельной работы 7 заданий. Для определения перечня задач необходимо знать номер своего варианта в группе, который объявляется преподавателем, ведущим практические занятия по высшей математике, и номер своей группы в потоке, который сообщает лектор потока. Зная эти данные, по таблице найдите номер задач, предлагаемых вашему варианту.
Учебное издание
МЕТОДИЧЕСКИЕ УКАЗАНИЯ
К САМОСТОЯТЕЛЬНОМУ ИЗУЧЕНИЮ ТЕМЫ
«ВЕКТОРНАЯ И ЛИНЕЙНАЯ АЛГЕБРА»
(для студентов всех специальностей)
Составитель ШМАНЁВА Лина Васильевна
Редактор Л.Н. Полчанникава
Тех. Редактор С.Х. Аниськова
Пл. изд. № 52 1991 г.
Подп. В печать
05.05.91. Формат 60![]() 84
84![]() .
Бумага тип. № 2. Офсетная печать. Усл.
Печ. Л. 0,93. Усл. Кр.-отт. 1,04. Уч.-изд. Л. 0,63.
Тираж 1050 экз. Зак. 4-4935.
.
Бумага тип. № 2. Офсетная печать. Усл.
Печ. Л. 0,93. Усл. Кр.-отт. 1,04. Уч.-изд. Л. 0,63.
Тираж 1050 экз. Зак. 4-4935.
Бесплатно.
КГМИ, 349104, Коммунарск, пр. Ленина, 16
ДМАПП, 340050, Донецк, ул. Артёма, 69
Бесплатно.
