§ 4. Плоскость

1. Общее уравнение плоскости

Всякое уравнение первой степени определяет в заданной прямоугольной системе координат плоскость.

Уравнение вида:

(27)

называется общим уравнением плоскости. Вектор , перпендикулярный плоскости, называется нормальным вектором плоскости.

2. Уравнение плоскости, проходящей через точку перпендикулярную вектору

Если плоскость проходит через точку перпендикулярно вектору, то её уравнение имеет вид:

(28)

3. Уравнение плоскости, проходящей через три точки в отрезках

Пусть плоскость проходит через точки ,,.

Имеет вид:

(29)

Если плоскость отсекает по осям координат соответственно отрезку ,, и, то её уравнение имеет вид:

(30)

4. Угол между плоскостями. Условия параллельности и перпендикулярности плоскостей

Угол между плоскостямииопределяется по формуле:

(31)

Условие параллельности плоскостей:

(32)

Условие перпендикулярности плоскостей:

(33)

5. Расстояние от точки до плоскости

Расстояние от точки до плоскостинаходится по формуле:

(34)

Пример 1. Составить уравнение плоскости, проходящей через точку перпендикулярно вектору.

Решение. Воспользуемся уравнением (28). Здесь ;;;;;.

Получим: или.

Пример 2. Найти отрезки, отсекаемые плоскостью на осях координат.

Решение. Преобразуем данноё уравнение плоскости к уравнению в отрезках (30) следующим образом:

;

Следовательно, величины отрезков, отсекаемых на осях, равны:

; ;

Пример 3. Найти расстояние между параллельными плоскостями и

Решение. Возьмём на одной из плоскостей произвольную точку и определим её расстояние от другой плоскости. Например, на первой плоскости выберем точку и найдём её расстояние до плоскости, пользуясь формулой (33):

Пример 4. Определить угол, образованный плоскостями и.

Решение. Воспользуемся формулой (31)

6. Вопросы для самопроверки

Как определяется общее уравнение плоскости?

Какой вектор называется нормальным к плоскости и как определяются его координаты из общего уравнения плоскости?

Как записывается уравнение плоскости, проходящей через точку перпендикулярно вектору?

Запишите уравнения плоскости через три точки; в отрезках.

Как определяется угол между плоскостями? Сформулируйте условия параллельности и перпендикулярности плоскостей.

Как определяется расстояние от точки до плоскости?

7. Примеры для самостоятельного решения

   1. Составить уравнение плоскости, проходящей через точку м перпендикулярной вектору.

   2. Составить уравнение плоскости, проходящей через точку и отсекающей равны отрезки на осях координат.

   3. Составить уравнение плоскости, проходящей через точки . Через точкупровести плоскость, параллельно плоскости.

   4. Составить уравнение плоскости, проходящей через точку перпендикулярно плоскостями.

   5. Найти угол между плоскостями и.

   6. При каких значениях иуравнения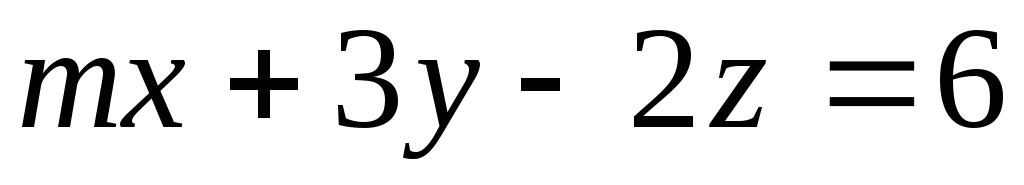иопределяют параллельные плоскости?

   7. При каком значении уравнениеиопределяют взаимно перпендикулярные плоскости?

   8. Найти высоту пирамиды , опущенную из вершинына грань АВС, если,,,. Указание. Данную высоту можно найти как расстояние от точкидо плоскости АВС.

   9. Найти длину перпендикуляра, опущенного из точки 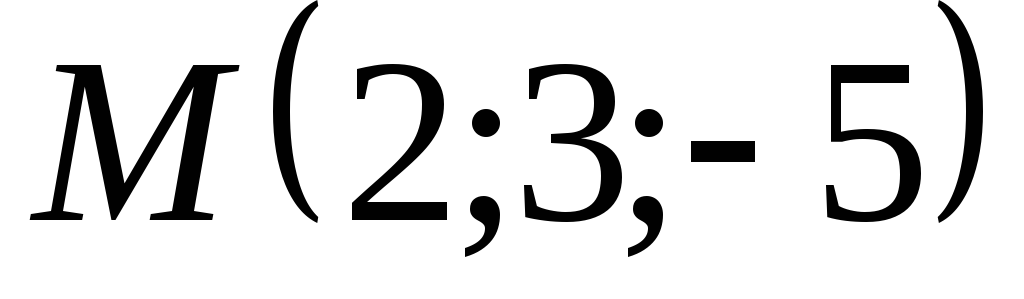на плоскость.

   10. Составить уравнение плоскостей, параллельных плоскости и отстоящих от неё на расстоянии

8. Ответы к примерам

4.7.1. . 4.7.2..

4.7.3. . 4.7.4..

4.7.5. . 4.7.6..

4.7.7. ;. 4.7.8..

4.7.9. . 4.7.10.,