Министерство высшего и среднего специального образования УССР

КОММУНАРСКИЙ ГОРНО-МЕТАЛУРГИЧЕСКИЙ ИНСТИТУТ

Методические указания

К самостоятельному изучению темы «ВЕКТОРНАЯ И ЛИНЕЙНАЯ АЛГЕБРА. ПРИЛОЖЕНИЯ К ЗАДАЧАМ АНАЛИТИЧЕСКОЙ ГЕОМЕТРИИ» по курсу «ВЫСШАЯ МАТЕМАТИКА»

Коммунарск КГМИ 1989

Министерство высшего и среднего специального образования УССР

КОММУНАРСКИЙ ГОРНО-МЕТАЛУРГИЧЕСКИЙ ИНСТИТУТ

Методические указания

К самостоятельному изучению темы «ВЕКТОРНАЯ И ЛИНЕЙНАЯ АЛГЕБРА. ПРИЛОЖЕНИЯ К ЗАДАЧАМ АНАЛИТИЧЕСКОЙ ГЕОМЕТРИИ» по курсу «ВЫСШАЯ МАТЕМАТИКА»

(для студентов всех специальностей)

Утверждено

На заседании кафедры

Высшей математики

Протокол № 10 от 13.04.88

Коммунарск КГМИ 1989

УДК 512.94 : 517.94

Методические указания к самостоятельному изучению темы «Векторная и линейная алгебра. Приложения к задачам аналитической геометрии» по курсу «Высшая математика» (для студентов всех специальностей) / Сост. Л.В. Шманёва. – Коммунарск: КГМИ, 1989. – 79 с.

Содержат подробное решение типовых задач по разделам высшей математики, а также примеры для самостоятельного решения. В конце каждой темы сформулированы вопросы для самопроверки, даны ответы предложенным упражнениям.

Составитель Л.В. Шманёва, ст. преп.

Рецензисты: Г.М. Финкельштейн, доц.

Е.Я. Косюга, ст. преп.

Методические указания состоят из 3 частей: 1 – элементы линейной алгебры, 2 – векторная алгебра, 3 – аналитическая геометрия на плоскости и пространстве.

В каждой части приводится краткий обзор теории, определения, формулы.

Цель работы – научится самостоятельно работать на практических занятиях и решать основные типы задач по указанным темам.

Часть 1. Элементы линейной алгебры

§ 1. Определители и их скойства

Литература: (1, с. 5-16; 2, с. 35-41; 3, с. 263-268)

1. Определители второго порядка

Определителем второго порядка называется число, обозначаемое символом и определяемое равенством

(1)

где ,,,- элементы определителя. Элементы снабжены двумя индексами: первый индекс обозначает номер строки, а второй – номер столбца, где находится данный элемент.

Пример 1.

2. Определители третьего порядка

Определителем третьего порядка называется число, которое обозначается символом и определяется равенством(2)

Пример 2.

Минором элементаопределителя третьего порядка называется определитель второго порядка, который получится, если в исходном определителе вычеркнуть строку и столбец, содержащие данный элемент (i-ю строку и j-й столбец).

Например:

- минор элемента ;

- минор элемента .

Алгебраическим дополнением элементаопределителя называется минор этого элемента, взятый со знаком

(3)

Тогда формулу (2) для вычисления определителя третьего порядка можно записать так

. (4)

Верна общая теорема: Определитель третьего порядка равен сумме произведений элементов любой строки или столбца на их алгебраические дополнения.

3. Свойства определителей

Определитель не изменится, если его строки заменить столбцами, а столбцы – соответствующими строками

Общий множитель какой-либо строки (или столбца) можно вынести за знак определителя

При перестановке двух строк (столбцов) знак определителя меняется на противоположный

Если элементы одной строки (столбца) определителя соответственно равны элементам другой строки (столбца) этого определителя, то определитель равен нулю.

Определитель не изменится, если к элементам одной строки (столбца) прибавить соответственные элементы другой строки (столбца), умноженные на одно и тоже число

4. Определители n-го порядка

Аналогично вводятся определители более высокого порядка, для которых справедливы те же свойства, что и для определителей второго и третьего порядков. Определитель n-го порядка имеет вид:

(5)

Пример 3. Вычислить определитель 4-го порядка:

Замечание. Используя свойство 5 и теорему о разложимости определителя по элементам какой-либо строки (столбца), можно свести вычисление определителя n-го порядка к определителю второго порядка, сделав в какой- либо строке (столбце) нули, кроме одного.

Пример 4.

Сделаем нули, кроме одного, в первом столбце, для этого из элементов второй строки вычтем удвоенные элементы первой строки; из элементов четвёртой строки – элементы первой. Таким образом, определитель 4-го порядка свелся к определителю 3-го порядка, в котором сделаем нули (кроме одного) во втором столбце, для чего к элементам второго столбца прибавим элементы первого, в результате получим определитель 2-го столбца.

1. Вопросы для самопроверки

1. Что называется определителем второго порядка, как он обозначается и считается?

2. Что называется определителем третьего порядка, как он обозначается и считается?

3. Что называется минором и алгебраическим дополнением элемента определителя и какая связь между ними?

4. Сформулируйте теорему о разложимости определителя по элементам какой-либо строки (столбца).

5. Каким свойством обладает определитель?

6. Что называется определителем более высокого порядка 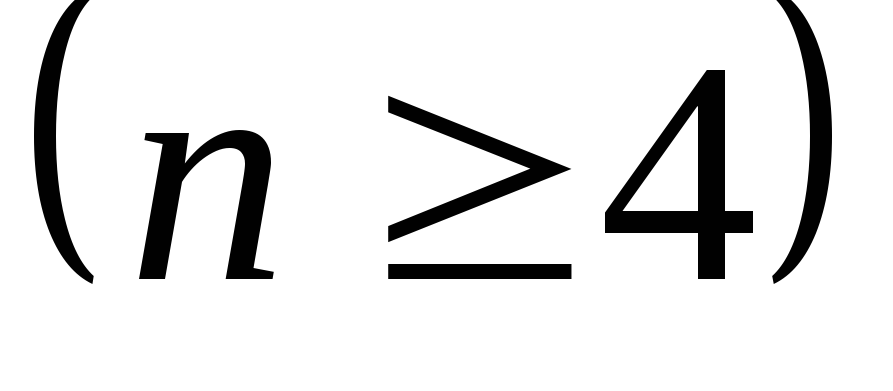и каким образом можно понизить порядок определителя?

6. Примеры для самостоятельного решения

Вычислите определители второго порядка:

1. 2.

3. 4.

5. 5.

Решить уравнения:

7. 8.

9. 10.

11. 12.

Решить неравенства:

13. 14.

15. 16.

Вычислите определители третьего порядка:

17. 18.

19. 20.

21. 22.

Решить уравнения:

23. 24.

Решить неравенства:

25. 26.

27. 28.

Вычислить определители 4-го порядка:

29. 30.

31. 32.

7. Ответы к примерам

1. 10; 2. ;

3. -1; 4. ;

5. ; 6.;

7. ; 8.;

9. ; 10.;

11. ; 12.,;

13. ; 14.;

15. [0;7]; 16.[-3;1];

17. -44; 18. -29;

19. -12; 20. 0;

21. ; 22.;

23. ,; 24.;

25. [3,5;]; 26.[10;2];

27. [;-6][-4;]; 28.[-2;1];

29. 30; 30. -20;

31. 0; 32. 48.