
- •Подпространства линейного пространства Определение линейного подпространства
- •Пересечение и сумма подпространств линейного пространства
- •Пересечение и сумма
- •Евклидово пространство
- •Норма матрицы
- •Объяснение «на пальцах»
- •Неравенство Коши — Буняковского
- •Неравенство треугольника
- •Евклидова геометрия
- •Ортогональная система
- •Ортогонализация
- •Ортогональное разложение
- •Ортонормированный базис
- •Ортогональные системы векторов
- •Свойства
- •Линейные операторы в евклидовом и унитарном пространствах
- •Собственные числа и собственные векторы линейного оператора
- •Правило отыскания собственных чисел и собственных векторов
Собственные числа и собственные векторы линейного оператора
Наиболее
просто устроены матрицы диагонального
вида
 .
Возникает вопрос, нельзя ли найти базис,
в котором матрица линейного оператора
имела бы диагональный вид. Такой базис
существует.
Пусть дано линейное
пространство Rnи действующий в
нем линейный оператор A; в этом случае
оператор A переводит Rnв себя, то
есть A:Rn→ Rn.
.
Возникает вопрос, нельзя ли найти базис,
в котором матрица линейного оператора
имела бы диагональный вид. Такой базис
существует.
Пусть дано линейное
пространство Rnи действующий в
нем линейный оператор A; в этом случае
оператор A переводит Rnв себя, то
есть A:Rn→ Rn.
Определение.Ненулевой
вектор
![]() называется
собственным вектором оператора A, если
оператор A переводит
называется
собственным вектором оператора A, если
оператор A переводит
![]() в
коллинеарный ему вектор, то есть
в
коллинеарный ему вектор, то есть
![]() .
Число λ называется собственным значением
или собственным числом оператора A,
соответствующим собственному вектору
.
Число λ называется собственным значением
или собственным числом оператора A,
соответствующим собственному вектору
![]() .
Отметим некоторые свойства собственных
чисел и собственных векторов.
1. Любая
линейная комбинация собственных векторов
.
Отметим некоторые свойства собственных
чисел и собственных векторов.
1. Любая
линейная комбинация собственных векторов
![]() оператора
A, отвечающих одному и тому же собственному
числу λ, является собственным вектором
с тем же собственным числом.
2.
Собственные векторы
оператора
A, отвечающих одному и тому же собственному
числу λ, является собственным вектором
с тем же собственным числом.
2.
Собственные векторы
![]() оператора
A с попарно различными собственными
числами λ1, λ2, …, λmлинейно независимы.
3. Если собственные
числа λ1=λ2= λm= λ, то
собственному числу λ соответствует не
более m линейно независимых собственных
векторов.
оператора
A с попарно различными собственными
числами λ1, λ2, …, λmлинейно независимы.
3. Если собственные
числа λ1=λ2= λm= λ, то
собственному числу λ соответствует не
более m линейно независимых собственных
векторов.
Итак, если имеется nлинейно
независимых собственных векторов
![]() ,
соответствующих различным собственным
числам λ1, λ2, …, λn, то
они линейно независимы, следовательно,
их можно принять за базис пространства
Rn. Найдем вид матрицы линейного
оператора A в базисе из его собственных
векторов, для чего подействуем оператором
A на базисные векторы:
,
соответствующих различным собственным
числам λ1, λ2, …, λn, то
они линейно независимы, следовательно,
их можно принять за базис пространства
Rn. Найдем вид матрицы линейного
оператора A в базисе из его собственных
векторов, для чего подействуем оператором
A на базисные векторы:
 тогда
тогда
 .
Таким образом, матрица линейного
оператора A в базисе из его собственных
векторов имеет диагональный вид, причем
по диагонали стоят собственные числа
оператора A.
Существует ли другой
базис, в котором матрица имеет диагональный
вид? Ответ на поставленный вопрос дает
следующая теорема.
.
Таким образом, матрица линейного
оператора A в базисе из его собственных
векторов имеет диагональный вид, причем
по диагонали стоят собственные числа
оператора A.
Существует ли другой
базис, в котором матрица имеет диагональный
вид? Ответ на поставленный вопрос дает
следующая теорема.
Теорема.Матрица
линейного оператора A в базисе
![]() (i
= 1..n) имеет диагональный вид тогда и
только тогда, когда все векторы базиса
- собственные векторы оператора A.
(i
= 1..n) имеет диагональный вид тогда и
только тогда, когда все векторы базиса
- собственные векторы оператора A.
Правило отыскания собственных чисел и собственных векторов
Пусть
дан вектор
![]() ,
где x1, x2, …, xn- координаты
вектора
,
где x1, x2, …, xn- координаты
вектора
![]() относительно
базиса
относительно
базиса
![]() и
и
![]() -
собственный вектор линейного оператора
A, соответствующий собственному числуλ, то есть
-
собственный вектор линейного оператора
A, соответствующий собственному числуλ, то есть
![]() .
Это соотношение можно записать в
матричной форме
.
Это соотношение можно записать в
матричной форме
![]() .
(*)
.
(*)
Уравнение
(*) можно рассматривать как уравнение
для отыскания
![]() ,
причем
,
причем
![]() ,
то есть нас интересуют нетривиальные
решения, поскольку собственный вектор
не может быть нулевым. Известно, что
нетривиальные решения однородной
системы линейных уравнений существуют
тогда и только тогда, когда det(A - λE) = 0.
Таким образом, для того, чтобы λ было
собственным числом оператора A необходимо
и достаточно, чтобы det(A - λE) = 0.
Если
уравнение (*) расписать подробно в
координатной форме, то получим систему
линейных однородных уравнений:
,
то есть нас интересуют нетривиальные
решения, поскольку собственный вектор
не может быть нулевым. Известно, что
нетривиальные решения однородной
системы линейных уравнений существуют
тогда и только тогда, когда det(A - λE) = 0.
Таким образом, для того, чтобы λ было
собственным числом оператора A необходимо
и достаточно, чтобы det(A - λE) = 0.
Если
уравнение (*) расписать подробно в
координатной форме, то получим систему
линейных однородных уравнений:
 (1)
где
(1)
где
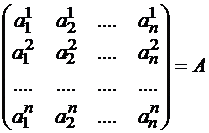 -
матрица линейного оператора.
-
матрица линейного оператора.
Система (1) имеет ненулевое решение, если ее определитель D равен нулю

Получили уравнение для нахождения собственных чисел. Это уравнение называется характеристическим уравнением, а его левая часть - характеристическим многочленом матрицы (оператора) A. Если характеристический многочлен не имеет вещественных корней, то матрица A не имеет собственных векторов и ее нельзя привести к диагональному виду. Пусть λ1, λ2, …, λn- вещественные корни характеристического уравнения, причем среди них могут быть и кратные. Подставляя по очереди эти значения в систему (1), находим собственные векторы.
Пример 12.Линейный
оператор A действует в R3по закону
![]() ,
где x1, x2, .., xn- координаты
вектора
,
где x1, x2, .., xn- координаты
вектора
![]() в
базисе
в
базисе
![]() ,
,
![]() ,
,
![]() .
Найти собственные числа и собственные
векторы этого оператора.Решение.Строим матрицу этого оператора:
.
Найти собственные числа и собственные
векторы этого оператора.Решение.Строим матрицу этого оператора: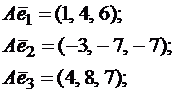
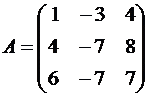 .
Составляем систему для определения
координат собственных векторов:
.
Составляем систему для определения
координат собственных векторов: Составляем
характеристическое уравнение и решаем
его:
Составляем
характеристическое уравнение и решаем
его: .
λ1,2= -1, λ3= 3.
Подставляя
λ = -1 в систему, имеем:
.
λ1,2= -1, λ3= 3.
Подставляя
λ = -1 в систему, имеем: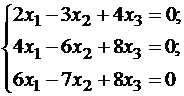 или
или
 Так
как
Так
как
 ,
то зависимых переменных два, а свободное
одно.
Пусть x1- свободное
неизвестное, тогда
,
то зависимых переменных два, а свободное
одно.
Пусть x1- свободное
неизвестное, тогда
 Решаем
эту систему любым способом и находим
общее решение этой системы:
Решаем
эту систему любым способом и находим
общее решение этой системы:
 Фундаментальная
система решений состоит из одного
решения, так как n - r = 3 - 2 = 1.
Множество
собственных векторов, отвечающих
собственному числу λ = -1, имеет вид:
Фундаментальная
система решений состоит из одного
решения, так как n - r = 3 - 2 = 1.
Множество
собственных векторов, отвечающих
собственному числу λ = -1, имеет вид:
![]() ,
где x1- любое число, отличное от
нуля. Выберем из этого множества один
вектор, например, положив x1= 1:
,
где x1- любое число, отличное от
нуля. Выберем из этого множества один
вектор, например, положив x1= 1:
![]() .
Рассуждая аналогично, находим
собственный вектор, отвечающий
собственному числу λ = 3:
.
Рассуждая аналогично, находим
собственный вектор, отвечающий
собственному числу λ = 3:
![]() .
В пространстве R3базис состоит
из трех линейно независимых векторов,
мы же получили только два линейно
независимых собственных вектора, из
которых базис в R3составить нельзя.
Следовательно, матрицу A линейного
оператора привести к диагональному
виду не можем.
.
В пространстве R3базис состоит
из трех линейно независимых векторов,
мы же получили только два линейно
независимых собственных вектора, из
которых базис в R3составить нельзя.
Следовательно, матрицу A линейного
оператора привести к диагональному
виду не можем.
Пример 13.Дана матрица
 .
1. Доказать, что вектор
.
1. Доказать, что вектор
![]() является
собственным вектором матрицы A. Найти
собственное число, соответствующее
этому собственному вектору.
2. Найти
базис, в котором матрица A имеет
диагональный вид.Решение.1. Если
является
собственным вектором матрицы A. Найти
собственное число, соответствующее
этому собственному вектору.
2. Найти
базис, в котором матрица A имеет
диагональный вид.Решение.1. Если
![]() ,
то
,
то
![]() -
собственный вектор
-
собственный вектор .
Вектор (1, 8, -1) - собственный вектор.
Собственное число λ = -1.
Диагональный
вид матрица имеет в базисе, состоящем
из собственных векторов. Один из них
известен. Найдем остальные.
Собственные
векторы ищем из системы:
.
Вектор (1, 8, -1) - собственный вектор.
Собственное число λ = -1.
Диагональный
вид матрица имеет в базисе, состоящем
из собственных векторов. Один из них
известен. Найдем остальные.
Собственные
векторы ищем из системы: Характеристическое
уравнение:
Характеристическое
уравнение:
 ;
(3 + λ)[-2(2-λ)(2+λ)+3] = 0; (3+λ)(λ2- 1) = 0
λ1= -3, λ2= 1, λ3= -1.
Найдем собственный вектор, отвечающий
собственному числу λ = -3:
;
(3 + λ)[-2(2-λ)(2+λ)+3] = 0; (3+λ)(λ2- 1) = 0
λ1= -3, λ2= 1, λ3= -1.
Найдем собственный вектор, отвечающий
собственному числу λ = -3: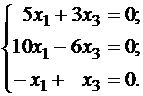 Ранг
матрицы этой системы равен двум и равен
числу неизвестных, поэтому эта система
имеет только нулевое решение x1=
x3= 0. x2здесь может быть
любым, отличным от нуля, например, x2= 1. Таким образом, вектор (0,1,0) является
собственным вектором, отвечающим λ =
-3. Проверим:
Ранг
матрицы этой системы равен двум и равен
числу неизвестных, поэтому эта система
имеет только нулевое решение x1=
x3= 0. x2здесь может быть
любым, отличным от нуля, например, x2= 1. Таким образом, вектор (0,1,0) является
собственным вектором, отвечающим λ =
-3. Проверим: .
Если λ = 1, то получаем систему
.
Если λ = 1, то получаем систему
 Ранг
матрицы равен двум. Последнее уравнение
вычеркиваем.
Пусть x3- свободное
неизвестное. Тогда x1= -3x3,
4x2= 10x1- 6x3= -30x3- 6x3, x2= -9x3.
Полагая
x3= 1, имеем (-3,-9,1) - собственный
вектор, отвечающий собственному числу
λ = 1. Проверка:
Ранг
матрицы равен двум. Последнее уравнение
вычеркиваем.
Пусть x3- свободное
неизвестное. Тогда x1= -3x3,
4x2= 10x1- 6x3= -30x3- 6x3, x2= -9x3.
Полагая
x3= 1, имеем (-3,-9,1) - собственный
вектор, отвечающий собственному числу
λ = 1. Проверка: .
Так как собственные числа действительные
и различны, то векторы, им отвечающие,
линейно независимы, поэтому их можно
принять за базис в R3. Таким образом,
в базисе
.
Так как собственные числа действительные
и различны, то векторы, им отвечающие,
линейно независимы, поэтому их можно
принять за базис в R3. Таким образом,
в базисе
![]() ,
,
![]() ,
,
![]() матрица
A имеет вид:
матрица
A имеет вид: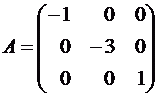 .
Не всякую матрицу линейного оператора
A:Rn→ Rnможно привести к
диагональному виду, поскольку для
некоторых линейных операторов линейно
независимых собственных векторов может
быть меньше n. Однако, если матрица
симметрическая, то корню характеристического
уравнения кратности m соответствует
ровно m линейно независимых векторов.
.
Не всякую матрицу линейного оператора
A:Rn→ Rnможно привести к
диагональному виду, поскольку для
некоторых линейных операторов линейно
независимых собственных векторов может
быть меньше n. Однако, если матрица
симметрическая, то корню характеристического
уравнения кратности m соответствует
ровно m линейно независимых векторов.
Определение.Симметрической
матрицей называется квадратная матрица,
в которой элементы, симметричные
относительно главной диагонали, равны,
то есть в которой
![]() .Замечания.1. Все собственные
числа симметрической матрицы вещественны.
2. Собственные векторы симметрической
матрицы, соответствующие попарно
различным собственным числам, ортогональны.
В качестве одного из многочисленных
приложений изученного аппарата,
рассмотрим задачу об определении вида
кривой второго порядка.
.Замечания.1. Все собственные
числа симметрической матрицы вещественны.
2. Собственные векторы симметрической
матрицы, соответствующие попарно
различным собственным числам, ортогональны.
В качестве одного из многочисленных
приложений изученного аппарата,
рассмотрим задачу об определении вида
кривой второго порядка.
Матрица линейного преобразования в базисе из собственных векторов
В
разделе "Матрица
линейного преобразования"
мы выяснили, что каждое линейное
преобразование
![]() -мерного
линейного пространства в фиксированном
базисе задается матрицей. Если меняется
базис, то, как правило, меняется и матрица.
Возникает вопрос, нельзя ли найти базис,
в котором матрица линейного преобразования
имеет наиболее простой вид. В общем
случае выбрать такой базис довольно
сложно. Это связано с нахождением
нормальной жордановой формы матрицы,
изложение которого можно найти в более
обстоятельных учебниках по линейной
алгебре, например, в [4],
[5].
Следующая теорема отвечает на этот
вопрос в более простом случае.
-мерного
линейного пространства в фиксированном
базисе задается матрицей. Если меняется
базис, то, как правило, меняется и матрица.
Возникает вопрос, нельзя ли найти базис,
в котором матрица линейного преобразования
имеет наиболее простой вид. В общем
случае выбрать такой базис довольно
сложно. Это связано с нахождением
нормальной жордановой формы матрицы,
изложение которого можно найти в более
обстоятельных учебниках по линейной
алгебре, например, в [4],
[5].
Следующая теорема отвечает на этот
вопрос в более простом случае.
Теорема
19.2
Пусть
![]() --
линейное преобразование
--
линейное преобразование
![]() -мерного
линейного пространства. Матрица линейного
преобразования имеет диагональный вид
-мерного
линейного пространства. Матрица линейного
преобразования имеет диагональный вид
|
|
(19.5) |
тогда
и только тогда, когда векторы базиса
являются собственнными векторами
преобразования
![]() ,
соответствующими собственным числам
,
соответствующими собственным числам
![]() .
.
Доказательство.
Пусть преобразование
![]() имеет
имеет
![]() линейно
независимых собственных векторов
линейно
независимых собственных векторов
![]() ,
соответствующих собственным числам
,
соответствующих собственным числам
![]() .
Так как векторы
.
Так как векторы
![]() линейно
независимы, то они образуют базис. Найдем
матрицу преобразования
линейно
независимы, то они образуют базис. Найдем
матрицу преобразования
![]() в
этом базисе. Ее первый столбец является
координатным столбцом вектора
в
этом базисе. Ее первый столбец является
координатным столбцом вектора
![]() .
Так как
.
Так как
![]() --
собственный вектор, то
--
собственный вектор, то
![]()
Координатный
столбец этого вектора
 .
Второй столбец матрицы
.
Второй столбец матрицы
![]() является
координатным столбцом вектора
является
координатным столбцом вектора
![]() .
Так как
.
Так как
![]() --
собственный вектор, то
--
собственный вектор, то
![]()
Координатный
столбец этого вектора
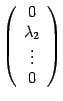 .
Вычисляя аналогично остальные столбцы,
получаем, что матрица линейного
преобразования
.
Вычисляя аналогично остальные столбцы,
получаем, что матрица линейного
преобразования
![]() в
базисе
в
базисе
![]() имеет
вид (19.5).
Первая часть теоремы доказана.
имеет
вид (19.5).
Первая часть теоремы доказана.
Пусть
в некотором базисе
![]() матрица
линейного преобразования имеет
вид (19.5).
Найдем образ вектора
матрица
линейного преобразования имеет
вид (19.5).
Найдем образ вектора
![]() .
Этот вектор имеет координатный столбец
.
Этот вектор имеет координатный столбец
 ,
его образ имеет координатный столбец
,
его образ имеет координатный столбец
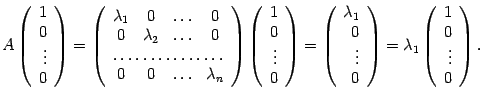
Следовательно,
![]() --
собственное число преобразования
--
собственное число преобразования
![]() ,
а
,
а
![]() --
соответствущий ему собственный вектор.
Аналогично находим, что любой базисный
вектор
--
соответствущий ему собственный вектор.
Аналогично находим, что любой базисный
вектор
![]() является
собственным вектором преобразования
является
собственным вектором преобразования
![]() ,
соответствующим собственному числу
,
соответствующим собственному числу
![]() .
.
Следствие
19.2
Если
у матрицы
![]() порядка
порядка
![]() существует
набор из
существует
набор из
![]() линейно
независимых собственнных векторов,
соответствующих собственным числам
линейно
независимых собственнных векторов,
соответствующих собственным числам
![]() ,
то матрица
,
то матрица
![]() подобна
диагональной матрице с числами
подобна
диагональной матрице с числами
![]() на
диагонали.
на
диагонали.
Теорема
19.3
Пусть
собственные векторы
![]() преобразования
преобразования
![]() соответствуют
собственным числам
соответствуют
собственным числам
![]() ,
среди которых нет равных друг другу.
Тогда система векторов
,
среди которых нет равных друг другу.
Тогда система векторов
![]() является
линейно независимой.
является
линейно независимой.
Доказательство.
Воспользуемся методом математической
индукции по числу векторов. Если
![]() ,
то утверждение теоремы следует из того,
что собственный вектор -- ненулевой.
,
то утверждение теоремы следует из того,
что собственный вектор -- ненулевой.
Пусть
утверждение верно для системы векторов
![]() .
Составим линейную комбинацию векторов
.
Составим линейную комбинацию векторов
![]() и
приравняем ее к нулю
и
приравняем ее к нулю
|
|
(19.6) |
К
обеим частям применим преобразование
![]()
![]()
По определению линейного преобразования получим
![]()
Так
как
![]() --
собственные векторы, то
--
собственные векторы, то
![]()
Умножим
равенство (19.6)
на
![]() и
вычтем из последнего равенства. Получим
и
вычтем из последнего равенства. Получим
![]()
Так
как по предположению индукции векторы
![]() линейно
независимы, то
линейно
независимы, то
![]()
По
условию
![]() ,
следовательно,
,
следовательно,
![]() .
Подставим эти значения в (19.6),
получим
.
Подставим эти значения в (19.6),
получим
![]() .
Получили, что из равенства (19.6)
следует
.
Получили, что из равенства (19.6)
следует
![]() ,
то есть векторы
,
то есть векторы
![]() линейно
независимы.
линейно
независимы.
Следствие
19.3
Если
матрица
![]() порядка
порядка
![]() имеет
имеет
![]() попарно
различных собственных чисел, то она
подобна диагональной матрице.
попарно
различных собственных чисел, то она
подобна диагональной матрице.

