
- •Подпространства линейного пространства Определение линейного подпространства
- •Пересечение и сумма подпространств линейного пространства
- •Пересечение и сумма
- •Евклидово пространство
- •Норма матрицы
- •Объяснение «на пальцах»
- •Неравенство Коши — Буняковского
- •Неравенство треугольника
- •Евклидова геометрия
- •Ортогональная система
- •Ортогонализация
- •Ортогональное разложение
- •Ортонормированный базис
- •Ортогональные системы векторов
- •Свойства
- •Линейные операторы в евклидовом и унитарном пространствах
- •Собственные числа и собственные векторы линейного оператора
- •Правило отыскания собственных чисел и собственных векторов
Линейные операторы в евклидовом и унитарном пространствах
Теорема.
Пусть
![]() --
линейный оператор в евклидовом (унитарном)
пространстве. Сопоставим ему билинейную
(полуторалинейную) функцию
--
линейный оператор в евклидовом (унитарном)
пространстве. Сопоставим ему билинейную
(полуторалинейную) функцию
![]() ,
,
![]() .
Это соответствие является биекцией
между операторами и билинейными
(полуторалинейными) функциями.
.
Это соответствие является биекцией
между операторами и билинейными
(полуторалинейными) функциями.
Рассмотрим
билинейную (полуторалинейную) функцию
![]() ,
заданную формулой
,
заданную формулой
![]() .
Тогда матрица для функции
.
Тогда матрица для функции
![]() в
ортонормированном базисе
в
ортонормированном базисе
![]() --
это матрица
--
это матрица
![]() ,
т.е.
,
т.е.
![]() .
Будем говорить, что функция
.
Будем говорить, что функция
![]() определяет
сопряженный
оператор
определяет
сопряженный
оператор
![]() .
Более подробно
.
Более подробно
Определение.
Сопряженным
оператором
к оператору
![]() называется
такой оператор
называется
такой оператор
![]() ,
который удовлетворяет равенству
,
который удовлетворяет равенству
![]() .
.
Определение.
Оператор
![]() называется
самосопряженным
или симметричным
(эрмитовым),
если
называется
самосопряженным
или симметричным
(эрмитовым),
если
![]() ,
т.е.
,
т.е.
![]() .
Оператор
.
Оператор
![]() называется
кососимметричным
(
косоэрмитовым),
если
называется
кососимметричным
(
косоэрмитовым),
если
![]() ,
т.е.
,
т.е.
![]() .
Оператор
.
Оператор
![]() называется
ортогональным
(унитарным
для
называется
ортогональным
(унитарным
для
![]() ),
если
),
если
![]() .
.
Теорема.
Пусть
![]() --
ортонормальный базис в евклидовом
(унитарном) пространстве
--
ортонормальный базис в евклидовом
(унитарном) пространстве
![]() ,
и
,
и
![]() --
линейный оператор. Оператор
--
линейный оператор. Оператор
![]() является
самосопряженным (эрмитовым)
тогда и только тогда, когда его матрица
является
самосопряженным (эрмитовым)
тогда и только тогда, когда его матрица
![]() в
базисе
в
базисе
![]() симметрична
симметрична
![]() (эрмитова
(эрмитова
![]() ).
).
14
ПРЕОБРАЗОВАНИЕ МАТРИЦЫ ЛИНЕЙНОГО ОПЕРАТОРА ПРИ ПЕРЕХОДЕ К НОВОМУ БАЗИСУ
Пусть
V
– линейное пространство, А
– линейный оператор из
![]() ,
,
![]() и
и
![]() –
два базиса в V
и
–
два базиса в V
и
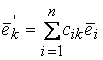 –
формулы перехода от базиса
–
формулы перехода от базиса
![]() к
базису
к
базису
![]() .
Обозначим через
.
Обозначим через
![]() матрицу
перехода от базиса к базису. Отметим,
что ранг матрицы С
равен n.
Пусть
матрицу
перехода от базиса к базису. Отметим,
что ранг матрицы С
равен n.
Пусть![]() и
и
![]() –
матрицы оператора А
в
указанных базисах.
–
матрицы оператора А
в
указанных базисах.
Теорема
7.1.
Матрицы
А
и
![]() оператора
А
в базисах
оператора
А
в базисах
![]() и
и
![]() связаны
соотношением
связаны
соотношением
![]() .
.
Доказательство.
При
воздействии линейного оператора А
вектор
![]() пространства
пространства
![]() переводится
в вектор
переводится
в вектор
![]() этого
пространства, т.е. справедливо равенство
этого
пространства, т.е. справедливо равенство
![]() =
А
=
А![]() (7.3)
(7.3)
(в старом базисе) и равенство
![]() =
А
=
А![]() (7.4)
(7.4)
(в
новом базисе). Так как
![]() –
матрица перехода от старого базиса к
новому, то
–
матрица перехода от старого базиса к
новому, то
![]() (7.5)
(7.5)
![]() (7.6)
(7.6)
Умножим
равенство (7.5) слева на матрицу
![]() ,
получим А
,
получим А![]() =
АC
=
АC![]() и
с учетом (7.3)
и
с учетом (7.3)
![]() =
АC
=
АC![]() .
Заменив левую часть полученного выражения
в соответствии с (7.6), получим: С
.
Заменив левую часть полученного выражения
в соответствии с (7.6), получим: С![]() =
АC
=
АC![]() или
или
![]() =
С–1
АC
=
С–1
АC![]() .
Сравнивая найденное выражение с
равенством (7.4), получим доказываемую
формулу.
.
Сравнивая найденное выражение с
равенством (7.4), получим доказываемую
формулу.
Отсюда следует, что определитель матрицы линейного оператора не зависит от базиса.
15
Переход от одного ортонормированного базиса к другому.
Согласно
определению 5.1.4. матрица
![]() ,
удовлетворяющая соотношению
,
удовлетворяющая соотношению
![]() ,
называется ортогональной, причём для
любой ортогональной матрицы справедливы
равенства
,
называется ортогональной, причём для
любой ортогональной матрицы справедливы
равенства
![]() =||E||
и
=||E||
и
![]() .
Кроме того, в евклидовом пространстве
будут справедливы следующие теоремы.
.
Кроме того, в евклидовом пространстве
будут справедливы следующие теоремы.
Ортогональные
матрицы (и только они) в
![]() могут
служить матрицами перехода от одного
ортонормированного базиса к другому.
могут
служить матрицами перехода от одного
ортонормированного базиса к другому.
Рассмотрим
два различных ортонормированных базиса
![]() и
и
![]() вE
вE![]() с матрицей перехода
с матрицей перехода
![]() от
первого базиса ко второму. Поскольку в
этих базисах матрица Грама единичная,
то из соотношения
от
первого базиса ко второму. Поскольку в
этих базисах матрица Грама единичная,
то из соотношения
![]() следует
равенство
следует
равенство
![]() ,
или
,
или
![]() .
Поскольку матрица перехода
.
Поскольку матрица перехода
![]() невырожденная,
то, окончательно, имеем
невырожденная,
то, окончательно, имеем
![]() .
.
В развернутой
форме равенство
![]() принимает
вид
принимает
вид
![]() ,
которое для частного случая
,
которое для частного случая
![]() было
получено в §2.9.
было
получено в §2.9.
Теорема доказана.
16
