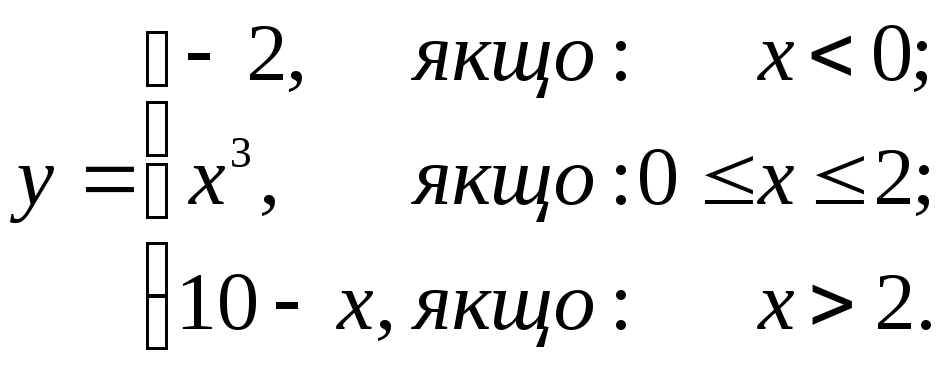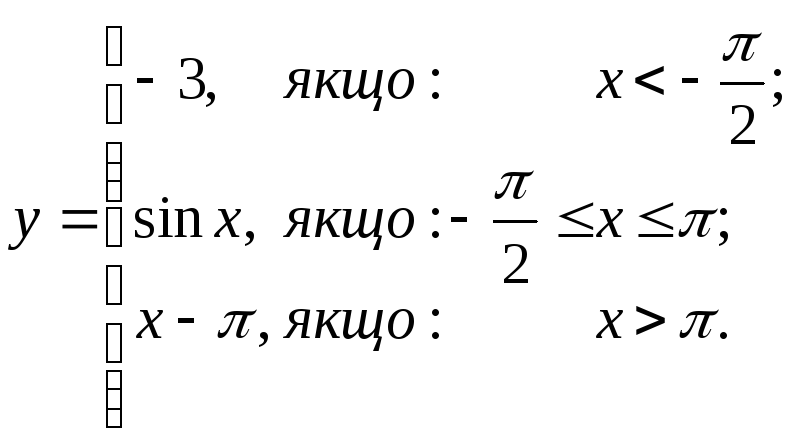7. Даны векторы в некотором базисе. Показать, что векторы образуют базис. Найти координаты вектора в этом базисе.
|
№ |
|
|
|
|
|
1 |
-2, 4, 7 |
0, 1, 2 |
1, 0, 1 |
-1, 2, 4 |
|
2 |
6, 2,-1 |
1, 3, 0 |
2,-1, 1 |
0,-1, 2 |
|
3 |
1,-4, 4 |
2, 1,-1 |
0, 3, 2 |
1,-1, 1 |
|
4 |
-9, 5, 5 |
4, 1, 1 |
2, 0,-3 |
-1, 2, 1 |
|
5 |
-5,-5, 5 |
-2, 0, 1 |
1, 3,-1 |
0, 4, 1 |
|
6 |
13, 2, 7 |
5, 1, 0 |
2,-1, 3 |
1, 0,-1 |
|
7 |
-9, -1, 7 |
0, 1, 1 |
-2, 0, 1 |
3, 1, 0 |
|
8 |
3,-3, 4 |
1, 0, 2 |
0, 1, 1 |
2,-1, 4 |
|
9 |
3, 3,-1 |
3, 1, 0 |
-1, 2, 1 |
-1, 0, 2 |
|
10 |
-1, 7,-4 |
-1, 2, 1 |
2, 0, 3 |
1, 1,-1 |
|
11 |
6, 5,-4 |
1, 1, 4 |
0,-3, 2 |
2, 1,-1 |
|
12 |
5,15, 0 |
1, 0, 5 |
-1, 3, 2 |
0,-1, 1 |
|
13 |
6,-1, 7 |
1,-2, 0 |
-1, 1, 3 |
1, 0, 4 |
|
14 |
2,-1,11 |
1, 1, 0 |
0, 1,-2 |
1, 0, 3 |
|
15 |
11, 5,-3 |
1, 0, 2 |
-1, 0, 1 |
2, 5,-3 |
|
16 |
8, 0, 5 |
2, 0, 1 |
1, 1, 0 |
4, 1, 2 |
|
17 |
3, 1, 8 |
0, 1, 3 |
1, 2,-1 |
2, 0,-1 |
|
18 |
8, 1,12 |
1, 2,-1 |
3, 0, 2 |
-1, 1, 1 |
|
19 |
-9,-8,-3 |
1, 4, 1 |
-3, 2, 0 |
1,-1, 2 |
|
20 |
-5, 9,-3 |
0, 1,-2 |
3,-1, 1 |
4, 1, 0 |
|
21 |
-5, 5,6 |
0, 5, 1 |
3, 2,-1 |
-1, 1, 0 |
|
22 |
8, 9, 4 |
1, 0, 1 |
0,-2, 1 |
1, 3, 0 |
|
23 |
23,-4,30 |
2, 1, 0 |
1,-1, 0 |
-3, 2, 5 |
|
24 |
3, 1, 3 |
2, 1, 0 |
1, 0, 1 |
4, 2, 1 |
|
25 |
-1, 7, 0 |
0, 3, 1 |
1,-1, 2 |
2,-1, 0 |
|
26 |
11,-1, 4 |
1,-1, 2 |
3, 2, 0 |
-1, 1, 1 |
|
27 |
0,-8, 9 |
0,-2, 1 |
3, 1,-1 |
4, 0, 1 |
|
28 |
-3, 2,18 |
1, 1, 4 |
-3, 0, 2 |
1, 2,-1 |
|
29 |
8,-7,-13 |
0, 1, 5 |
3,-1, 2 |
-1, 0, 1 |
|
30 |
2, 7, 5 |
1, 0, 1 |
1,-2, 0 |
0, 3, 1 |
8. Вычислить (без правила Лопиталя) границы:
1). 
2). 
.
3). 
.
4). 
.
5). 
.
6). 
.
7). 
.
8). 
.
9). 
.
10). 
; 
.
11). 
12). 
13). 
14). 
15). 
16). 
17). 
18). 
19). 
20). 
21). 
22). 
23). 
24). 
25). 
26). 
27). 
28). 
29). 
30). 
9. Исследовать на непрерывность функцию и классифицировать точки разрыва:
|
1).
|
2). |
|
3).
|
4).
|
|
5).
|
6).
|
|
7).
|
8).
|
|
9).
|
10).
|
|
11).
|
12). |
|
13). |
14).
|
|
15).
|
16).
|
|
17).
|
18).
|
|
19).
|
20).
|
|
21).
|
22).
|
|
23). |
24). |
|
25).
|
26).
|
|
27).
|
28).
|
|
29).
|
30).
|
10. Найти производные данных функций:
1). 
2). 
3). 
4). 
5). 
6). 
7). 
8). 
9). 
10). 
11). 
12). 
13). 
14). 
15). 
16). 
17). 
18). 
19). 
20). 
21). 
22). 
23). 
24). 
25). 
26). 
27). 
28). 
29). 
30). 
11. Провести полное исследование функций и построить их графики:
1). 
2). 
3). 
4). 
5). 
6). 
7). 
8). 
9). 
10). 
11). 
12). 
13). 
14). 
15). 
16). 
17). 
18). 
19). 
20). 
21). 
22). 
23). 
24). 
25). 
26). 
27). 
28). 
29). 
30). 
