Электротехника / СХА,ЭТ,КП / СВ,фильтры

Напряжение постоянного тока, получаемого путем выпрямления переменного напряжения, характеризуется двумя параметрами: действующим (средним) значением Ud и коэффициентом пульсации К_П :

, где (1) U1_m - амплитуда первой гармоники переменной составляющей напряжения при разложении сигнала в ряд Фурье.

Схемы выпрямления (СВ) для синусоидального однофазного напряжения дают постоянное напряжение с коэффициентами К_Псв =1.57 для однополупериодного выпрямления и К_Псв = 0.67 для двухполупериодного выпрямления.

Для современных электротехнических устройств (компьютеров, приемопередатчиков, усилителей и т.д.) требуется напряжение питания с К_П << 1. Следовательно, СВ не могут обеспечивать их питание напряжением постоянного тока без устройств, уменьшающих величину пульсаций.

Для уменьшения К_П на выходе СВ используются емкостные и индуктивные фильтры.

На рис1. представлена в общем виде расчетная схема для рассмотрения работы фильтров, где обозначено:

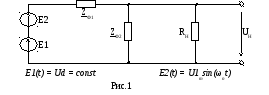
Е1 – источник питания постоянного тока с ЭДС, равной среднему значению выпрямленного напряжения

Е2(t) – источник питания переменного тока с амплитудой, равной амплитуде первой гармоники при разложении переменной составляющей выпрямленного напряжения в ряд Фурье U1_m и частотой f_П , равной частоте пульсации выпрямленного напряжения;

Z_ф1 и Z_ф2 – комплексное сопротивление фильтров включенных последовательно (Z_ф1) и параллельно (Z_ф2) нагрузке;

Rн и Uн – сопротивление нагрузки и напряжение нагрузки.

Очевидным требованием к Uн, является максимальное значение постоянной составляющей и минимальное значение переменной составляющей. Этому условию соответствует:

Для Ф1 – минимальное значение сопротивления для постоянного тока и максимальное для переменного, т.е. индуктивное сопротивление (Z_L = Z_Ф1 = ω_пL_ф >>R_H).

Для Ф2 – максимальное значение сопротивление для постоянного тока и минимальное для переменного, т.е. емкостное сопротивление (Z_C= Z_Ф2 =1/(ω_пС_ф >>R_H).

Следовательно, индуктивные фильтры включаются последовательно нагрузке, емкостные – параллельно.

В сложных радио электронных и вычислительных устройствах наибольшее распространение нашли емкостные фильтры. Рассмотрим работу такого фильтра на примере однофазной однополупериодной СВ (рис.2)

На рис.2. обозначено:

Т1 – трансформатор питания

U1, f1 - действующее значение напряжения сети и частота сети;

U2 – действующие значение на вторичной обмотке трансформатора;

VD1 - выпрямительный диод

С_ф - емкость фильтра;

Rн – сопротивление нагрузки;

Uн; К_Пн – средние значение напряжения нагрузки и коэффициент пульсаций напряжения нагрузки. Диод, обозначенный пунктиром, служит для того, чтобы условно получить выпрямленное напряжение u_d(t) при отсутствии фильтра и сопротивления нагрузки для пояснения работы схемы.

Временные диаграммы, поясняющие работу схемы, представлены на рис.3.

На рис.3а представлена временная диаграмма переменного напряжения на вторичной обмотке трансформатора u2(t) и обозначено:

U2m, U2 – максимальное и действующее значения напряжения;

T1=1/f1 – период переменного напряжения;

t, α – текущее время и соответствующий ему фазовый угол.

На рис.3б представлена временная диаграмма выпрямленного напряжения u_d(t) и обозначено:

Ud_m Ud_m - максимальное и действующее значения выпрямленного напряжения при отсутствии фильтра и сопротивления нагрузки.

На рис.3в представлена временная диаграмма напряжения нагрузки U_H(t) и обозначено:

U_H,U_Hmin , U_Hmax – среднее (действующее), максимальное и минимальное напряжения нагрузки.

Рассматриваемая СВ является нелинейной за счет наличия диода с нелинейной вольтамперной характеристикой (ВАХ), поэтому методы расчета линейных схем для нее неприменимы .Для простоты рассмотрения будем считать, что выходное сопротивление СВ равно нулю, диод VD1 имеет идеальную ВАХ, а момент включения СВ в работу соответствует началу положительной полуволны выпрямленного напряжения (точка «0»).

При включении питания напряжение на конденсаторе и сопротивлении нагрузки при открытом диоде VD1 будет возрастать по синусоиде выпрямленного напряжения (рис.3в, участок 0-1 временной диаграммы).

При уменьшении выпрямленного напряжения u_d(t) потенциал на диоде VD1 станет меньше потенциала на конденсаторе, и диод закроется. При этом конденсатор в точке 2 будет заряжен до значения Uнm и будет обладать максимальным запасом энергии

. (2)

На убывающем участке напряжения U2 (участок 1-2 ) диод VD1 будет закрыт за счет того, что напряжение заряда конденсатора Сф, приложенная к катоду диода, будет превышать значение напряжения на выходе СВ, приложенная к аноду. В этом случае расчетная схема будет иметь вид, представленный на рис.4.

Схема представленная на рис. 4, описывается однородным линейным дифференциальным уравнением с нулевой правой частью, причем начальные условия (напряжение на конденсаторе) ненулевые ( U_C(0) = U2_max ):

, (3)

где: i(t) - ток в цепи;

- напряжение на конденсаторе;

- напряжение на сопротивлении нагрузки.

Согласно расчетной схеме, эти напряжения равны между собой и соответствуют напряжению нагрузки. Если считать за нулевой момент время, соответствующее точке1, то решение уравнения (3) относительно напряжения нагрузки будет иметь вид

, (4)

что соответствует – линии 1-2 на временной диаграмме.

Касательная, проведенная к экспоненте 1-5 в точке 1 (линия 1-5) на временной оси отсекает отрезок времени

, (5)

который называется постоянной времени фильтра.

Если бы импульс выпрямленного синусоидального напряжения был единственным, то Uн с течением времени стремилось бы к нулю по экспоненте (линия 1-6). Но при периодическом повторении импульсов с частотой f_П и периодом Т_П=1/ f_П, в момент времени, когда напряжение нагрузки станет меньше напряжения очередного синусоидального импульса (точка 3), диод откроется и начнется заряд конденсатора Сф по нарастающему фронту синусоиды до достижения максимального значения. После этого начнется цикл разряда конденсатора, затем снова цикл разряда и т.д. Таким образом, процесс будет иметь периодический установившийся характер.

Следовательно, сигнал напряжения нагрузки можно разложить в ряд Фурье и определить для него среднее значение и амплитуду первой гармоники. Но для сигнала указанной формы расчетные соотношения получаются слишком громоздкими и неудобными для практического использования.

На рис.5 представлены временные диаграммы процессов в схеме источника постоянного напряжения, причем данные диаграммы построены по точным аналитическим выражениям в программе MATHCAD14 при следующих параметрах схемы:

U2 = 10 B; U2_max = U_Фmax = 10*√2 = 14,1 B; f1 = 50 Гц; R_H = 400 Ом; C_Ф = 100 мкФ.

. Рис.5

На рис. 5 показаны следующие временные диаграммы:

U1(t) – выпрямленное напряжение при отсутствии фильтра;

U3(t) – напряжение нагрузки;

U4(t) – представление напряжения нагрузки в виде пилообразного напряжения;

U2(t) – среднее значение напряжения нагрузки U4(t) (U_Нср ≈ 10,5 В);

U5(t) – касательная к U3(t) в точке максимума, соответствующая линии 1-5 на рис.3. Данная касательная от точки максимума до точки пересечения с осью t отсекает на оси t отрезок времени τ_ф = С_Ф­∙R_Н = 100∙10^-6∙400 = 0,04 с.

Из рис.3 следует, что для обеспечения малых значений К_П должно выполняться соотношение

τ_Ф= R_HC >> Т_П , (6)

где Т_П – период пульсаций.

Поэтому, можно считать, что на промежутке времени, равному периоду пульсаций, процесс носит не экспоненциальный, а линейный характер, и разложить сигнал в ряд Тейлора с учетом постоянной составляющей и члена первого порядка:

, (7)

что соответствует сигналу U4(t) на рис.5. Линия U5(t) является касательной к U4(t) в точке максимума U3(t) и показывает, что за период пульсаций расстояние по оси времени от точки максимума до момента пересечения касательной оси времени составляет промежуток τ_Ф=R_HC=400*100*10^-6=0,04 с.

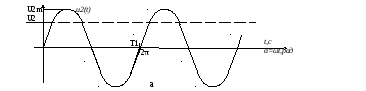
Если считать, что процесс зарядки конденсатора происходит за бесконечно малый временной интервал, то временную диаграмму переменной составляющей напряжения нагрузки можно представить в виде пилообразного напряжения. На рис.6 представлены временные диаграммы для этого случая переменной составляющей напряжения в зависимости от фазового угла (рис.6а) и от времени (рис.6б).

Данный сигнал за период напряжения пульсаций Т_П =1/ f_П (или в угловых величинах в пределах –π ≤ α ≤+π) можно разложить в ряд Фурье. Причем среднее значение напряжения при К_П << 1 можно считать равным максимальному значению

U_Н ≈ U_Нmax ≈ U_Фmax ≈ U2∙√2. (8)

С учетом того, что в пределах периода сигнал симметричен относительно начала координат, разложение в ряд Фурье будет иметь только синусные составляющие, а амплитуды гармоник в функции фазового угла будут определяться по формуле

, (9)

n- порядковый номер гармоники;

Un_max – амплитуда n-гармоники;

К – коэффициент наклона прямой.

Следовательно, амплитуду первой гармоники во временной области можно определить по соотношению

(10)

Знак минус в выражении (10) указывает на то, что разлагаемая в ряд функция является убывающей, и им в дальнейшем пренебрегаем.

Воспользовавшись соотношением (1) можно определить значение коэффициента пульсаций для выходного напряжения: (11)

Для рассматриваемого случая определим коэффициент пульсаций:

Рассмотренная методика определения Кп является приближенной. Для оценки погрешности его вычисления можно воспользоваться точными соотношениями определения амплитуды первой гармоники для сигнала U3(t). Математические соотношения, по которым построены временные диаграммы на рис.5 приведены в приложении 1.

Ниже представлены формулы в программе МС для определения амплитуд синусной и косинусной составляющих первой гармоники с разложения в ряд Фурье сигнала U3(t), суммарной амплитуды первой гармоники, среднего значения сигнала и коэффициента пульсаций.

Амплитуда синусной составляющей

Амплитуда косинусной составляющей

Суммарная амплитуда первой гармоники

Среднее значение напряжения U3(t) за период пульсаций

Точное значение коэффициента пульсаций

Сравнив полученное точное значение со значением, полученным по (11) можно сделать вывод, что данные значения практически совпадают. Следовательно, соотношение (11) можно использовать для определения коэффициента пульсаций.

На рис.7 приведены временные диаграммы представления напряжения нагрузки путем разложения сигнала в ряд Фурье с учетом 1, 5 и 100 гармоник ряда. Последнее представление практически совпадает с пилообразным напряжением U3(t) (рис.5).

Рис.7

Из (11) можно определить значение емкости фильтра, обеспечивающего требуемое значение коэффициента пульсаций

. (12)

Проделав аналогичные выкладки можно получить формулу для определения коэффициента пульсаций L- фильтра или расчета его индуктивности для обеспечения требуемого значения коэффициента пульсаций:

(13)

, (14)

причем постоянная времени L-фильтра определяется по соотношению

(15)

Эффективность фильтров оценивается коэффициентом сглаживания

(16)

где и - амплитуды первых гармоник на входе и на выходе фильтра. Очевидно, что при использовании фильтров и одинаковыми параметрами их эффективность при работе с различными схемами выпрямления будет различной, т.к. у них неодинаковая частота пульсаций.

Приведенные формулы используются для определения параметров фильтров при расчетах вторичных источников питания. Исходными данными для расчетов являются:

- диапазон изменения напряжения нагрузки;

- диапазон изменения тока нагрузки; - частота сети переменного синусоидального напряжения;

- допустимое значение коэффициента пульсаций напряжения нагрузки.

Методика расчетов при этом следующая

1. Для емкостного фильтра определяют минимальное значение эквивалентного сопротивления нагрузки, а для индуктивного – максимальное:

R_Hmin = U_Hmin/I_Hmax , R_Hmax = U_Hmax/I_Hmin. (17)

2. В зависимости от числа фаз выпрямленного напряжения n и числа полупериодов выпрямления m для конкретного вида СВ определяют частоту пульсаций выходного напряжения фильтра по формуле f_П = f1∙m∙n . (18)

3. По соотношениям (12) или (14) рассчитывают величину емкости или индуктивности для соответствующего фильтра.

При необходимости определения коэффициента пульсаций реального устройства необходимо пользоваться осциллографом. На рис.8 приведена модель рассматриваемого источника питания в программе Electronics Workbench.

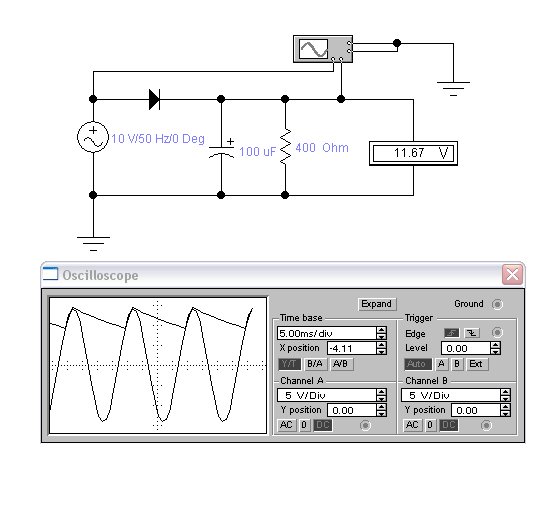
Рис.8

В рассматриваемой модели по каналу А на экран осциллографа выведено переменное напряжение с обмотки трансформатора ( u2(t) ), а по каналу В- напряжение нагрузки ( u_н(t) ). Воспользовавшись настройками осциллографа можно определить максимальное и минимальное значения напряжения нагрузки:

U_Hmax ≈ 14 B, U_Hmin≈ 9 B,

а показания вольтметра составляют 11,67 В. Значения коэффициента пульсаций можно рассчитать по любой из приведенных формул:

или

где U_V – показания вольтметра.

Анализ численных значений коэффициента показывает, что имеется различие в их значениях при различных методиках расчетов, но следует учесть тот факт, что невозможно оценить погрешности модели цепи в программе Electronics Workbench.

Приложение 1. Используемый математический аппарат программы MATHCAD.

ПРИМЕЧАНИЕ: при переносе формул из программы МС в WORD символ С_Ф отображается как No , а символ R_H – как Ri.
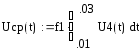