
- •Математическая логика и теория алгоритмов
- •11. Понятие об алгоритмах. Схемы алгоритмов
- •11.1. Понятие об алгоритме и теории алгоритмов
- •11.2. Схемы алгоритмов
- •11.3. Рекурсивные функции
- •11.4. Машина Тьюринга
- •11.5. Машина Поста
- •11.6. Нормальные алгорифмы а.А. Маркова
- •11.7. Универсальная абстрактная машина
- •11.8. Разрешимость в теории алгоритмов. Проблема самоприменимости
- •11.9. Сложность алгоритма
- •11.10. Представление схемы алгоритма эквивалентным автоматом
- •11.11. Представление схемы алгоритма микропрограммой с двумя типами микрокоманд
- •12. Элементы формальной логики
- •12.1. Предмет формальной логики
- •12.2. Понятие и его виды
- •12.3. Отношения между понятиями
- •12.4. Операции над понятиями
- •12.5. Суждение и его характеристика
- •Модальные и категорические суждения.
- •Простые категорические суждения.
- •Виды простых категорических суждений.
- •Распределение терминов в простом категорическом суждении.
- •Логический квадрат.
- •13. Умозаключение
- •13.1. Виды умозаключений
- •13.2. Непосредственное умозаключение
- •Умозаключения путем противопоставления предикату.
- •13.3. Опосредованное дедуктивное умозаключение. Фигуры силлогизма
- •Фигуры пкс.
- •Модусы пкс.
- •13.4. Дополнительные виды силлогизмов
- •13.5. Индуктивные умозаключения. Математическая индукция
- •14. Логика высказываний
- •14.1. Семантика логики высказываний
- •I закон – тождества.
- •14.3. Формализация высказываний
- •14.4. Интерпретации, разрешимость, выполнимость, общезначимость
- •14. 5. Логическая равносильность. Законы логики
- •14.6. Формы представления формул логики высказываний
- •14.7. Проблема дедукции в логике высказываний
- •15. Проверка правильности логических выводов. Метод резолюций
- •15.1. Закон контрапозиции
- •15.2. Логическое следование. Проверка правильности логических выводов
- •15.3. Силлогизмы в логике высказываний
- •Разделительно-категоричные силлогизмы.
- •16. Синтаксис и семантика языка логики предикатов
- •16.1. Понятие предиката
- •16.2. Кванторы и связанные переменные
- •16.3. Синтаксис языка логики предикатов. Формулы логики предикатов и формализация суждений
- •16.4. Семантика формул логики предикатов
- •Общезначимость, выполнимость, невыполнимость.
- •17. Тождественные преобразования формул логики предикатов
- •17.1. Операции над предикатами
- •17.2. Основные равносильности логики предикатов
- •Отрицание предложений с кванторами.
- •17.3. Тождественные преобразования формул
- •17.4. Универсум Эрбрана
- •18. Использование метода резолюций в логике предикатов
- •18.1. Подстановка и унификация
- •18.2. Резольвенция и факторизация
- •18.3. Метод резолюций в логике предикатов
- •18.4. Принцип логического программирования
- •19. Логические исчисления
- •19.1. Понятие о формальных теориях
- •19.2. Исчисление высказываний
- •19.3. Исчисление предикатов
- •19.4. Система натурного вывода
- •19.5. Понятие о математической лингвистике
- •19.6. Формальный язык
- •19.7. Формальные грамматики и их свойства
- •19.8. Теоремы Гёделя
- •20. Неклассические логики
- •20.1. Современные модальные логики
- •20.2. Понятие о теории неопределенности
- •20.3. Элементы теории нечетких множеств и нечеткая логика
- •20.4. Нечеткие алгоритмы
- •Литература
- •Приложение 1 Варианты контрольных заданий по дисциплине «Дискретная математика»
- •Приложение 2 Варианты контрольных заданий по дисциплине «Математическая логика»
13.5. Индуктивные умозаключения. Математическая индукция
Научная индукция – основывается на специальном математическом аппарате, например, на теории вероятностей и математической статистике. Эти методы призваны исключить случайность в выводе.
Математическая индукция – позволяет по некоторой обозримой области объектов с помощью индукционных шагов сделать общее заключение.
Пример. Получить методом математической индукции формулу суммы n первых нечетных чисел [5].

Проверим эту закономерность. Сделаем индукционный шаг: допустим, что эта формула соблюдается для n, следовательно, она соблюдается и для n+1. Докажем это:
![]()
![]() ,
что и требовалось доказать, следовательно,
формула верна для всех n.
,
что и требовалось доказать, следовательно,
формула верна для всех n.
14. Логика высказываний
14.1. Семантика логики высказываний
Если в формальной логике суждения расчленяются на субъект и предикат, то в логике высказываний суждение не расчленяется, а рассматривается как простое, из которого с помощью логических операций строится сложное суждение. С логики высказываний и началась собственно математическая логика.
В логике высказываний используется понятие «Высказывание».
Высказывание – это предложение, которое либо истинно, либо ложно. Высказывание – как правило, повествовательное предложение. Если нет общего мнения об истинности, то это не является высказыванием. Из двух и более высказываний строятся сложные высказывания, с помощью логических операций, рассмотренных ранее (см. «Переключательные функции и способы их задания»):
Конъюнкция: (логическое «И», «логическое умножение»). Обозначения: , , &, AND.
Дизъюнкция (логическое «ИЛИ», «логическое сложение»). Обозначения: , OR.
Импликация («если…, то», «тогда, когда»). Обозначения: , , , IF – THEN.
Эквиваленция (логическое «тогда и только тогда, когда»). Обозначения: , , EQV.
Разделительное «или» (неравнозначность или «сумма по модулю 2», или «исключающее или»). Обозначение: , XOR.
Инверсия (логическое «НЕ», «неверно, что»). Унарная операция. Обозначения: , , NOT.
Особое внимание в логике уделяется импликации, левый член называется антецедент, а правый – консеквент: XY=XY. В логике высказываний переменные обозначаются прописными буквами.
«Штрих Шеффера» и «Стрелка Пирса» – бинарные операции, с помощью которых могут быть выражены все другие операции.
Штрих
Шеффера (логическое «И-НЕ»). Обозначение:
|, A|B=![]() .
.
Стрелка
Пирса (логическое «ИЛИ-НЕ»). Обозначение:
,
АВ=![]() .
.
Символы логических операций называются пропозициональными знаками, а символы переменных – пропозициональными переменными.
В основании математической логики лежат законы Аристотеля. Они уже нам знакомы.
I закон – тождества.
В процессе определенного рассуждения каждое понятие и суждение должно быть тождественно само себе.
Х≡Х или ХХ.
II закон – противоречия.
Невозможно, что одно и то же, в одно и то же время, было и не было присуще одному и тому же в одном и том же отношении.
![]() (ложно),
(ложно),
![]() (истина).
(истина).
III закон – исключенного третьего.
Равным образом не может быть ничего промежуточного между двумя членами противоречия, а относительно чего-то одного необходимо, чтобы то ни было, либо утверждать, либо отрицать.
![]() (истина).
(истина).
Часть логиков считают, что в ситуациях относительных к будущему закон исключенного третьего не применим. Но это уже неклассическая логика.
IV закон – достаточного основания.
Всякая истинная мысль должна быть достаточно обоснована.
Напомним другие основные законы:
Закон идемпотентности.
ХХ≡Х;
ХХ≡Х.
Закон Де Моргана.
![]()
![]()
Закон двойного отрицания.
![]() .
.
14.2. Синтаксис логики высказываний.
Формулы логики высказываний
Логика тесно связана с языком, поэтому ему уделяется большое внимание.
Искусственные языки, создаваемые для научных целей, например, для науки логики, называются формализованными языками. При этом задается алфавит, где каждая последовательность символов называется словом. Затем вводится синтаксис – правила, позволяющие определять правильные слова, которые называются формулами [29].
Алфавит логики высказываний состоит из:
высказывательных или пропозициональных переменных (X, Y, Z, …, W);
логических констант (0 – ложь, 1 – истина);
символов логических операций (, |, , ,,
 …);
…);служебных символов, например, символов скобок ( [, ], {, }, (, )).
Определение формулы:
всякая высказывательная переменная – формула;
всякая логическая константа – формула;
если F1 и F2 – формулы, то формулами являются F1F2, F1F2, F1F2,
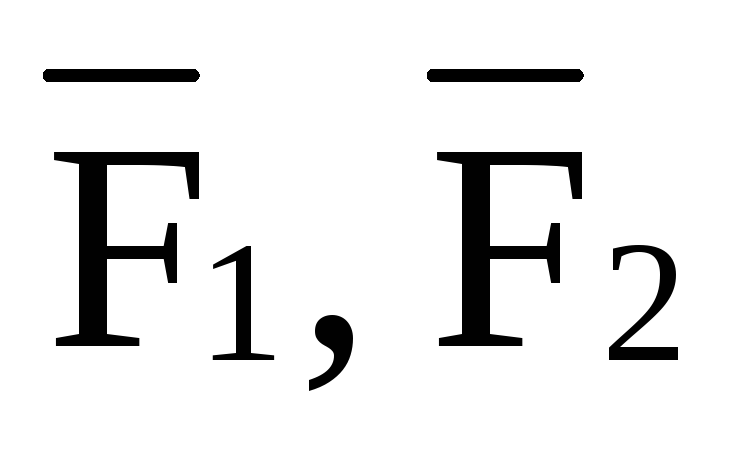 ,…(т.е.
при наличии знака операции над
формулами).
,…(т.е.
при наличии знака операции над
формулами).
Для обозначения переменных и формул, в математической логике приняты прописные буквы
Язык, служащий для объяснения другого языка, называется метаязыком. На таком языке (на естественном русском) написан этот подраздел.
