
- •Инновационный евразийский университет
- •Кафедра «Математика и информатика» Инновационный евразийский университет
- •Содержание (нужно разбить на главы после завершения)
- •Глава 1 Случайные события и их вероятности
- •Тема 1. Случайные события
- •1. Понятие испытаний, события
- •2. Виды случайных событий, пространство элементарных событий
- •3.Теоретико-множественная трактовка, алгебра событий
- •1. ;
- •Тема 2. Элементы комбинаторики и применение
- •1. Правило суммы и произведения.
- •2. Размещение с повторениями
- •3. Размещения без повторений, перестановки, подстановки
- •4. Cочетания, бином Ньютона
- •Тема 3. Определение вероятности, относительная частота, аксиоматическое определение вероятности
- •1. Классическое определение вероятности
- •2. Статистическое определение вероятности
- •3. Геометрическое определение вероятности
- •4. Аксиоматическое определение вероятности
- •5. Конечное вероятностное пространство
- •Тема 4. Теорема суммы вероятностей, формула полной системы событий, условная вероятность, теорема умножения вероятностей
- •2. Теорема умножения вероятностей
- •3. Применение комбинаторики к подсчёту вероятностей
- •4. Теоретические задачи.
- •5. Принцип практической невозможности маловероятных событий
- •Тема 5. Формула полной вероятности, вероятности гипотез,
- •1. Формула полной вероятности (фпв)
- •2. Вероятность гипотез (формулы Байеса).
- •3. Повторные испытания, схема Бернулли
- •4. Наиболее вероятностное число успехов
- •Тема 6. Предельные теоремы в схеме Бернулли,
- •1. Предельная теорема Пуассона
- •2. Простейший поток событий
- •3. Формула для геометрического закона распределения вероятности
- •5. Локальная теорема Муавра – Лапласа
- •6. Интегральная теорема Муавра - Лапласа
3.Теоретико-множественная трактовка, алгебра событий
Определим основные понятия теории вероятностей, следуя теоретико-множественному подходу, разработанные академиком Колмогоровым А.Н. в 1933 году.
Пусть производится некоторый опыт
(эксперимент) со случайным исходом.
Множество![]() всех возможных взаимоисключающих
исходов данного опыта называетсяпространством элементарных событий,
а сами исходы
всех возможных взаимоисключающих
исходов данного опыта называетсяпространством элементарных событий,
а сами исходы
![]() являются элементарными событиями (или
«элементами», «точками» пространства
являются элементарными событиями (или
«элементами», «точками» пространства![]() ).
).
Случайным событием
![]() (или просто событием) называется любое
подмножество множества
(или просто событием) называется любое
подмножество множества![]() ,
если
,
если![]() конечное или счетное (т.е. элементы этого
множества можно пронумеровать с помощью
множества натуральных чисел), при этом
считается
конечное или счетное (т.е. элементы этого
множества можно пронумеровать с помощью
множества натуральных чисел), при этом
считается![]() .
.
Элементарные события, входящие в
подмножество
![]() пространства
пространства![]() ,
называютсяблагоприятствующимисобытиями ксобытию
,
называютсяблагоприятствующимисобытиями ксобытию
![]() .
.
Множество
![]() всегда являетсядостоверным событием.Ему благоприятствует любое элементарное
событие, которое в результате данного
опыта непременно произойдёт.
всегда являетсядостоверным событием.Ему благоприятствует любое элементарное
событие, которое в результате данного
опыта непременно произойдёт.
Пустое множество
![]() всегда являетсяневозможным событием,
то есть в результате данного опыта
оно произойти не может. Над событиями
можно определить основные операции
существующие для множеств.
всегда являетсяневозможным событием,
то есть в результате данного опыта
оно произойти не может. Над событиями
можно определить основные операции
существующие для множеств.
Пусть
![]() являются
элементами пространства
являются
элементами пространства![]() .
.
В формулировках многих задач при случайном выборе (чего-либо) часто употребляется слова «наудачу», «случайным образом». Эти слова означает, что все комбинации элементов, которые могут быть выбраны в рассмариваемом эксприменте, равновозможны.
Приведем основные алгебраические
операции над событиями в данном
элементарном пространстве
![]() .
.
Суммой (или объединением)
двух событий![]() и
и ![]() называется такое событие, которое
выражает появление хотя бы одного из
событийА или В, и обозначаетсяА+В (или АВ).Другими словами, под событиемА+Впонимают событие, которое произошло
при тех исходах, когда произошло или
событие
называется такое событие, которое
выражает появление хотя бы одного из
событийА или В, и обозначаетсяА+В (или АВ).Другими словами, под событиемА+Впонимают событие, которое произошло
при тех исходах, когда произошло или
событие![]() или событие
или событие![]() или оба произошли одновременно, т.е.
произошло хотя бы одно из событий
или оба произошли одновременно, т.е.
произошло хотя бы одно из событий![]() или
или![]() .
Достоверное событие
.
Достоверное событие![]() изображается прямоугольником, элементарные
случайные события-точками прямоугольника.
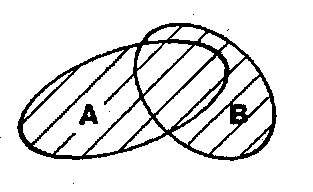
На рисунке 1, приведенадиаграммаЭйлера-Венна
для сложения двух событий по аналогии
с операцией сложения двух множеств:
изображается прямоугольником, элементарные
случайные события-точками прямоугольника.
На рисунке 1, приведенадиаграммаЭйлера-Венна
для сложения двух событий по аналогии
с операцией сложения двух множеств:
![]()
рис. 1
Произведениемдвух событий![]() и
и ![]() называется событие, состоящее из тех
элементарных исходов, которые одновременно
входят как вА так иВ (обозначаетсяА·В (или
называется событие, состоящее из тех
элементарных исходов, которые одновременно
входят как вА так иВ (обозначаетсяА·В (или![]() ).
Другими словами,А·В означает
событие, при котором событияА иВ
происходят одновременно. Действие
произведения над событиями можно
наглядно иллюстрировать с помощьюдиаграммы Эйлера-Венна.Достоверное
событие
).
Другими словами,А·В означает
событие, при котором событияА иВ
происходят одновременно. Действие
произведения над событиями можно
наглядно иллюстрировать с помощьюдиаграммы Эйлера-Венна.Достоверное
событие![]() изображается прямоугольником, случайное
событие - областью внутри прямоугольника.
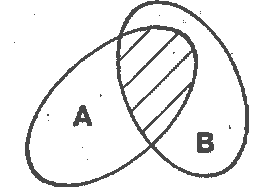
Действие произведения над событиями
можно изобразить геометрически, оно
показано на рис. 2.
изображается прямоугольником, случайное
событие - областью внутри прямоугольника.
Действие произведения над событиями
можно изобразить геометрически, оно
показано на рис. 2.
![]()
![]()
рис. 2
Пример. Каждый из трех стрелков произвел по одному выстрелу по цели. ПустьА–выражает попадание в цель первым стрелком,В– вторым стрелком иС– третьим стрелком. Нужно раскрыть смысл следующих событий:
