3. Геометрическое определение вероятности

Рассмотрим на плоскости некоторую область , имеющую площадь, и внутри областиподобластьс площадью(см. рисунок 3)

В области случайно выбирается точкаX.Этот выбор можно интерпретировать какбросаниеточкиХв область, при этом попадание точки в областьдостоверное событие, а в подобластиD- случайное событие. Предполагается все точки областиравноправны (все элементарные события равновозможные) и брошенная точка может попасть в любую точку из области_,и вероятность попадания в областьDпропорциональна площади этой области при этом, не зависит от её расположения и формы. Пусть событие, т.е. брошенная точка, попадёт в областьD.

Геометрической вероятностью события называется отношение площади областик площади области, т.е.

Геометрическое определение вероятности события применимо и в случаях, когда области иDлинейные или объёмные. Тогда соответстветствующие вероятности определяются равенствами:

;

где длина,объём области. Объединяя все три формулы можно сформулировать следующее общее определение.

Геометрической вероятностьюсобытияА называется отношение меры области (g), благоприятствующих, появлению событияАк мере всей рассматриваемой области (G), т. е

.

Заметим, что это определение, удовлетворяет всем трём условиям, классического определения вероятности (проверьте самостоятельно!).

Пример 5. На плоскости начерчены две концентрические окружности, радиусы которых соответственно 5 и 10 см. Найти вероятность того, что точка, брошенная наудачу в большой круг, попадет в кольцо, образованное построенными окружностями. Предполагается, что вероятность попадания точки в плоскую фигуру пропорциональна площади этой фигуры и не зависит от ее расположения относительно большого круга.

Решение.Площадь кольца (фигурыg): .

Площадь большого круга (фигуры G): .

Искомая вероятность равна .

Пример 5. (Задача о встрече) Два человека договорились о встрече между 12 и 13 часов дня. Условились, что тот, который придёт первым, ждёт второго в течение 15 мин, после чего уходит (если не встретились). Найти вероятность того, что встреча состоится, если каждый на удачу выбирает момент своего прихода.

Решение. Пустьвремя прихода первого человека, авремя прихода второго человека. Возможные значенияи:(в качестве единиц масштаба возьмём минуты), которые на плоскостиопределяют квадрат со стороной, равной 60. Точки этого квадрата изображают время встречи людей,(см. рис.5).

Тогда вероятное пространство выражается областью: все исходы в _-равновозможные, так как лица приходят наудачу. Обозначим через А событие, когда встреча лиц произойдёт, если разность между моментами их прихода будет не более 15 мин по обсалютной величине, следовательно,Неравенство

определяет область точек (на чертеже -заштрихованная область , которая благоприятствуют исходам встрече двух лиц.

Таким образом, искомая вероятность определяет геометрическую вероятность и определяется формулой

,

где соответственно площадь, области , а площадь областиравнаСледовательно

.

Задание.Эту же задачу решите самостоятельно в предположениях:

1. 10 минутного время ожидания первого лица пришедшего на встречу.

2. 45 минутного время ожидания первого лица пришедшего на встречу.

3. Сравните полученные результаты (вероятности)!

4. Если вероятностное пространство ито верна формула

В качестве следующего примера для геометрической вероятности рассмотрим задачу.

Задача 1. Стержен длиноюпроизвольным образом ломают на три части. Какова вероятность того, что из этих частей можно составить треугольник (событиеA)?

Решение. Обозначим черезидлины концевых частей стерженя(рис. 6); длина третьей части будет равнаВозможные значенияисвязаны условиями:

(1)

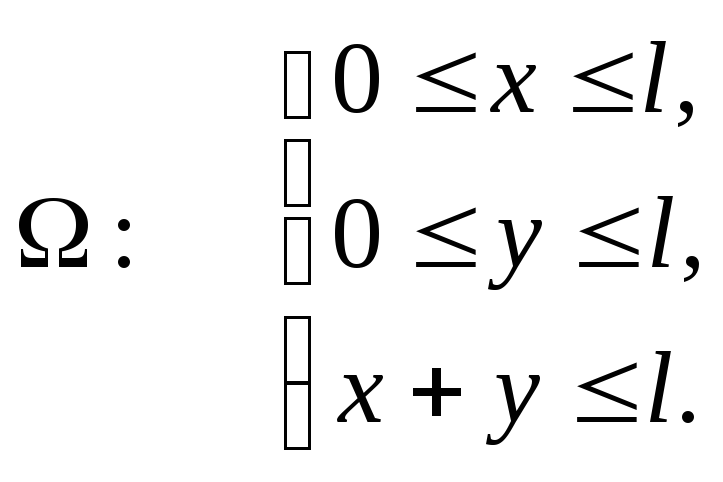
Данная система неравенств определяет на координатной плоскости область. Для того чтобы из трёх частей стерженя можно было сложить треугольник, необходимо и достаточно выполнение условий: каждая сторона треугольника должно быть меньше чем суммы двух других сторон треугольника, т.е. выполняются неравенства

(2) (g):

Система неравенств (2) выделяют из области подобласть, где записано условие, что каждая сторона треугольника должна быть меньше суммы двух других (см. рис.7). Согласно нашему способу разбиения (оно произвольное) легко заметить, что площадь областиравна четвёртой части площади областиОбластьсостоит из четырёх равных частей (треугольников). Следовательно, по формуле геомерической вероятности (основанием для этого служит «произвольность» разлома стержня) получим:

.

рис.7

Задача 2. В сигнализатор поступают сигналы от двух устройств, при этом поступление каждого из сигналов, равновозможно в любой момент промежутка времени длительностью . Моменты поступления сигналов независимы один от другого. Сигнализатор срабатывает, если разность между моментами поступления сигналов меньше

Найти вероятность того, что сигнализатор сработает за время (событие, если каждое устройство пошлёт по одному сигналу.

Решение. Обозначим моменты поступления сигналов первого и второго устройства через иВ силу условия задачи должны выполнятся двойные неравенства:

(3) .

Рассмотрим прямоугольную систему координат В этой системе двойное неравенство (3) выделяет область (квадрат):, координаты точек которой, представляют возможные значения элементов поступления сигналов первого и второго устройства

Сигнализатор срабатывает, если разность между моментами поступления сигналов меньше т.е.,

(4)

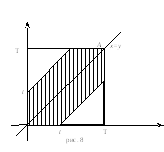
Система неравенств (4) указывают на область , куда поподают сигналы. Эта область указана на рисунке 8 и все точки, координаты которых удовлетворяют системе неравенств (4) принадлежать заштрихованному шестиграннику. Следовательно, этот шестигранник можно рассматривать как фигуру, координаты точек которой являются благоприятствующими моментами времении.

Искомая вероятность определяется равенством

Теперь мы можем рассмотреть аксиоматическое определение вероятности.