3. Примеры вычисления характеристических функций

3.1. Характеристическая функция биномиального закона.

Пусть с.в. , распределена по биномиальному закону. Найти, а затем выразить,, через. Имеет место утверждение.

Теорема 13.5. Для характеристической функции д.с.в., распределённой по биномиальному закону справедлива формула

(17) .

Доказательство.По определению случайная величинапринимает целочисленные значенияс вероятностями. На основании формулы (9) и формулы бинома Ньютона, находим

,

и с учётом , равенство (17) доказано.

Упражнение. Для математического ожидания и дисперсии биномиального распределения и при любом целом,вывести на основании равенства (12) формулы:

1.

2.

3.2. Характеристическая функция закона Пуассона.

Теорема 13.6. Для характеристической функции д.с.в., распределённой по закону Пуассона справедлива формула

(18) .

Доказательство. Согласно условию теоремы с.в.принимает только неотрицательные целые значения, при этом

Найдём характеристическую функцию с.в.

.

Следовательно, теорема доказана.

Упражнение. Для математического ожидания и дисперсии распределения Пуассона при любом целом, ина основании равенства (12) – (15) вывести формулы:

1.2.

Рассмотрим следующую теоретическую задачу, которая раскрывает ещё одну сторону закона Пуассона, где распределение происходит с параметром, равным произведению .

Задача [см. Бородин]. Число космических частиц, попадающих в аппаратный отсек ракеты за время её полёта распределено по закону Пуассона с параметром . При этом условная вероятность для каждой из этих частиц попасть в уязвимый блок равна.

Найти закон распределения количества частиц, попадающих в уязвимый блок.

Решение. Пусть обозначает уязвимый блок ракеты, авыражает наступление события, когда в уязвимый блок ракеты попалочастиц, иобозначает аппаратный отсек ракеты, авыражает наступления событий, когда в аппаратный отсек ракеты попалочастиц. Тогда события,, составляют полную группу событий, по формуле полной вероятностии с учётом того, что для, имеем

Далее, т.к. вероятности гипотез согласно условию задачи равны

, а для случаев , величинаопределяется по биномиальному закону с вероятностью «успеха» (частица попала в уязвимый блок). Поэтому, согласно формуле,Таким образом, окончательно получим

,

отсюда на основании значения биномиальных коэффициентов , получим

.

Таким образом, количество частиц, попадающих в уязвимых блок ракеты также распределены по закону Пуассона, но с параметром, равным произведению .

Напомним, что аналогичными формулами мы раньше встречались в пунктах 6.2. и 9.2. в связи вероятностью наступления потока события в случайные моменты времени (простейшие потоки событий).

3.3. Характеристическая функция геометрического закона.

Пусть проводится неограниченное число независимых одинаковых испытаний, в каждом из которых событие наступает с вероятностьюи пустьобозначает с.в. , равная числу испытаний до момента первого наступления события. Тогда эта вероятность как мы уже знаем (см. п.9.3.) равна

.

Это распределение называется геометрическим,так как вероятность, как числовая последовательность образуют геометрическую прогрессию. Тогда вероятность того, что событиенаступит не раньше момента, задаётся формулой

Так как производящая функция данного распределения (см.п.8.8.) равна , то согласно равенству (10) длябудем иметь

.

Упражнение. Для математического ожидания и дисперсии геометрического закона распределения на основании формул (12) – (15) вывести равенства:

1.2.

3.4. Характеристическая функция равномерного закона.

Вспомним, что равномерное распределение для любых вещественных чисел задается плотностью

Характеристическая функция равномерного распределения вычисляется следующим образом:

В частности, для центрально - симметрического отрезка получим

Следствие 4. В частности, справедливы равенства

Упражнение. Для математического ожидания и дисперсии равномерного распределения на основании формул (12) – (15) вывести равенства:

1.2.

Для случаявывести формулы:3. 4.

3.5. Характеристическая функция показательного закона.

Как было показано в.9.6. плотность с.в. , распределённая по показательному закону

имеет вид:

Характеристическая функция показательного распределения вычисляется следующим образом:

Упражнение. Для математического ожидания и дисперсии показательного распределения на основании формул (12) – (15) вывести равенства:

1.2.

3.6. Характеристическая функция нормального закона ().

Теорема 13.7. Для характеристической функции с.в., распределённой по нормальному закону справедлива формула

(19) .

Доказательство.Согласно формулы (29), пункта 9.9 функция плотности с.в.определена равенством

Характеристическая функция нормального распределения вычисляется следующим образом:

.

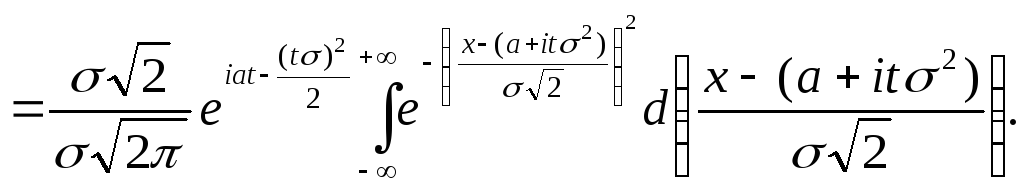Воспользуемся интегралом Пуассона , в итоге для характеристической функции с.в. получим равенство

.

Следствие 5. Для целых значений и всех значения параметрасправедлива формула

.

Пример 1. Для математического ожидания и дисперсии с.в., на основании формул (12) – (15) выведем равенства:

1..

2.=.

Применим формулу (12):

1., т.е..

2.

,

т.е. Получили известные нам результаты. Следовательно, с учётом с.к.о.эти параметры полностью определяют случайные величины, распределённые по нормальному закону.

Из рассмотренных примеров на предмет нахождения характеристических функций случайных величин (дискретных и непрерывных) непосредственно следует, что по законам распределения и функциям плотности, а следовательно, по функциям распределения с.в. всегда можно найти её характеристическую функцию.

Оказывается, имеет место и обратное предположение: а именно по характеристической функции однозначно определяется функция распределения. Рассмотрим ещё два утверждения, относящиеся к формулам «обращения и единственности».

Теорема 13.8 (формулы обращения). Справедливы следующие утверждения:

1.Если с.в. принимает целочисленные значениято

(20)

где мнимая единица,.

2. Если характеристическая функция случайной величиныабсолютно интегрируема, то существует плотности распределенияопределяемая формулой

(21) .

Доказательство. Заметим, что для любого целого числаи вещественногоимеют место равенства

(22)

Действительно, пусть любое вещественное число. Дляравенство очевидно. При любомимеем

,

где мы воспользовались равенством

Используя наше равенство для случая , исогласно, определению характеристической функции с.в.с целыми значениями, получим (с учётом того, что для отрицательных индексов вероятностиопределены)

Тем самым первый пункт теоремы доказан. Перейдём к доказательству второго пункта.

Так как функция абсолютно интегрируема, то для любыхс учётом формулы (22) имеем

(23) .

Используя определение характеристической функции (см. формулу (11)), получим

(24)

(23) .

Используя определение характеристической функции (см. формулу (11)), получим

(24)

На основании значения интеграла Дирихле (см. Лекции по математ. анализ Архипов и др. гл. 17. Лекция 20.)

,

где функция определяется равенствами:

Следовательно, получим равенства

.

Поэтому, по отдельности рассматривая случаи и

, получим

Пусть иточки непрерывности функции. Тогда приправая часть равенства (24)

стремится к равенству

Учитывая это равенство и на основании (23) и (24), имеем

(25) .

Поскольку функция распределения непрерывна слева, то с помощью предельного перехода из последовательности точек непрерывности ифункцииравенство (25) распространяется на произвольные точкии. Теперь из (25) по определению следует, чтоявляется плотностью функции распределении. В итоге, из равенства (23) получим предельное равенство.

В точках инепрерывности функциисправедливо равенство

(26) .

Равенство (26) носит название «формулы обращения». Она используется для вывода весьма важного утверждения -теорема единственности.

Упражнение. Пустьнатуральное число,целое число. Докажите, что

справедливы равенства

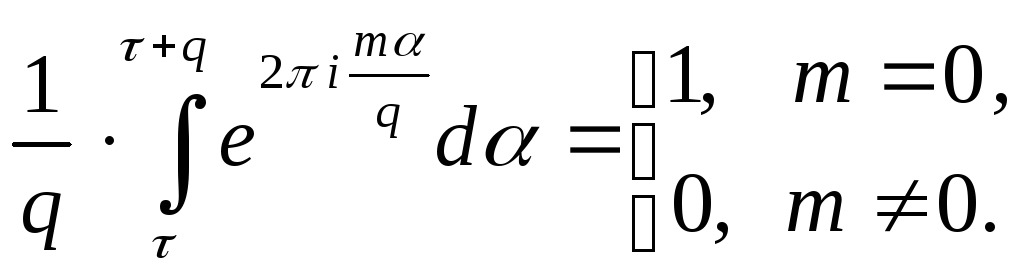
Теорема 13. 9 (единственности). Функция распределения однозначно определяется своей характеристической функцией.

Доказательство. Действительно, из равенства (26) непосредственно следует, что в каждой точке непрерывности функцииприменима формула

.

В последнем интеграле предел относительноберётся относительно множеству точекявляющихся точками непрерывности функции.

Рассмотрим некоторые примеры приложения последней теоремы.

Пример 2. Пусть независимые случайные величиныираспределены по закону Пуассона, причём

.

Покажем, что с.в. распределена по закону Пуассона с параметром.

В теореме 13.6 мы показали, что (см. (18)) . Отсюда имеем

,.

В силу теоремы 13.6. характеристическая функция суммы с.в. равна

,

т.е. является характеристической функцией некоторого закона Пуассона. Согласно теореме 13.9 единственное распределение, имеющее своей характеристической функцией, есть закон Пуассона, для которой вероятность определена равенством

Замечание. Математиком Д. А. Райковым была доказана более глубокое (обратное) утверждение:если сумма двух независимых с.в. распределена по закону Пуассона, то каждое слагаемое также распределена по закону Пуассона, т.е. верно и обратное утверждение.

Пример 3. Если независимые с.в. ираспределены по нормальному закону, то их

сумма также распределена нормально.

Действительно, если то соответствующие их характеристические функции определяются (см. (19)) равенствами

,

На основании теоремы 13.7 имеем

.

Это выражение является характеристическая функция нормального закона с математическим ожиданием и дисперсией. На основании теоремы единственности заключаем, что функция распределения с.в. нормальна.

В качество следующего примера без доказательства сформулируем ещё одно важное свойство характеристических функций.

Пример 4. Характеристическая функция вещественна тогда и только тогда, когда соответствующая ей функция распределения симметрична, другими словами, когда при любом функция распределения удовлетворяет равенству

Доказательство (см. [1], глава 7, параграф 33]).

Теория характеристических функций весьма интересная и имеет множество изящных применений в математике и её приложениях. Но мы этим ограничимся.