3. Примеры Марковских цепей

Большое число процессов: физических, биологических, в случайные блуждания системы, модели теории запасов, ветвящиеся процессы, различные модели в генетике и многие экономические явления описываются Марковскими цепями. Ниже приведём некоторые примеры.

А. Пространственно однородные марковские цепи

Пусть дискретная случайная величина принимает неотрицательные целочисленныезначения, причёмиПустьпредставляют результаты независимых наблюдений с.в..

Опишем две различные марковские цепи, связанные с последовательностью . В обоих случаях пространство состояний совпадает с множеством неотрицательных целых чисел.

1. Определим процесс, положивс заданным начальным значением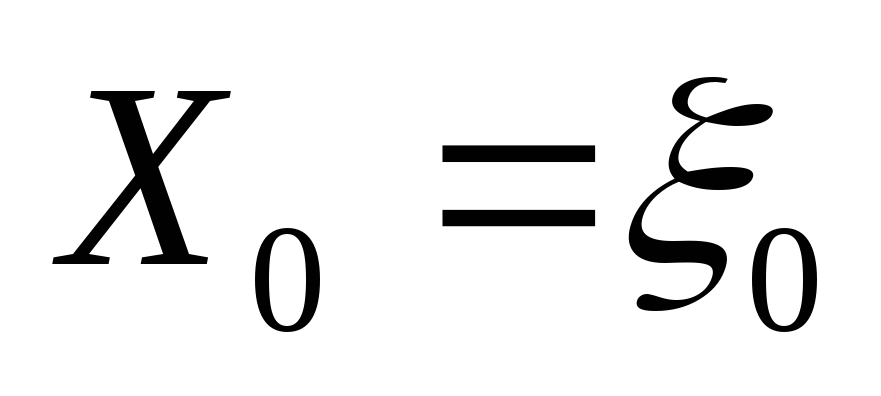. Матрица переходных вероятностей этого процесса имеет вид

Тот факт, что в этом процессе у матрицы все строки одинаковы, означает , что случайная величинане зависит от с.в..

II.Следующий важный класс Марковских цепей возникает при рассмотрении последовательных частичных суммслучайных величин, т.е.

.

Согласно определению считаем . Нетрудно заметить, что этот процесс, является марковским. Найдём его матрицу переходных вероятностей: именно с учётом независимостьюполучим

Следовательно, матрица переходных вероятностей будет иметь вид

(52)

Замечание. Если случайная величинаможет принимать как положительные, так и отрицательные целочисленные значения, т.е. для каждогозначениесодержатся в множестве целых чисел, то в этом случае пространство состояний удобнее отожествить со всеми целыми числами (а не преобразовывать в множество неотрицательных целых). Тогда матрицу переходных вероятностей удобно представить в более симметричной форме

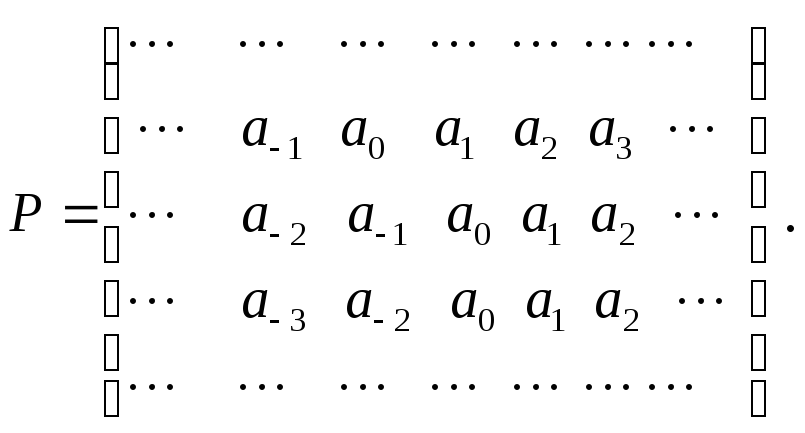
где и.

4. Расчет цепи Маркова для стационарного режима

Для нахождения финальных вероятностей необходимо составить систему алгебраических уравнений исходя из правила: для стационарного режима суммарный поток, переводящий систему из других состояний в состояние равен суммарному потоку вероятностей событий, выводящих систему из состояния

(53) .

К этим уравнениям надо добавить нормировочное условие , отбросив любое (одно) из уравнений. Полученная система уравнений снеизвестными имеет единственное решение.

Пример 4. Вычислительная машина находится в одном из следующих состояний:

система исправно работает;

система неисправна, тестируется;

система неисправна, настраивается программное обеспечение;

система находится на профилактике;

система ремонтируется, модернизируется;

Размеченный граф состояний системы показан на рисунке

(Кн. Белов …стр 63)

Составить систему алгебраических уравнений и найти предельные вероятности состояний.

Решение. Рассмотрим состояниесистемы в размеченном графе. В это состояние направлено две стрелки, следовательно, на основании (53) в левой части уравнения для

будут два слагаемых. Из этого состояния выходит одна стрелка, следовательно, в правой части уравнения будет одно слагаемое. Таким образом, получаем первое уравнение системы:

Аналогично запишем ещё три уравнения для оставшихся состояний (вершин графа):

В качестве пятого уравнения возьмём нормировочное уравнение . При решении системы уравнение дляотбрасываем. Его можно в конце использовать для контроля полученного решения. Таким образом, перепишем систему уравнений в виде:

В результате решения системы методом подстановок получим:

.

Замечание. Для решения этого примера нам не потребовались вероятности «задержек»

Пример 5. В локальной вычислительной сети работают три ЭВМ. По истечению определённого промежутка временивсе ЭВМ тестируются, в результате чего каждая из них признаётся либо исправленной, либо требующего ремонта. Вероятность того, что за время

исправная ЭВМ выйдет из строя, равна , а вероятность того, что неисправная будет отремонтирована, равна. Процессы выхода ЭВМ из строя и их восстановление протекают независимо друг от друга. Пологая

Найти предельные (финальные) вероятности.

Решение. Сначала построим граф состояний (см.рис.).

Рис. 1.15из книги Белов и…стр.64

Пронумеруем состояний системы по числу неисправных ЭВМ:

ни одной неисправной;одна неисправна;

две неисправны;все три неисправны;

Для того чтобы система перешла из состояния в состояние, нужно, чтобы одна из трёх ЭВМ за времявышла из строя.

Эта вероятность в соответствии с законом распределения Бернулли равнаАналогично, находим:

.

Для того, чтобы система из состояния перешла в состояние, нужно, чтобы неисправная ЭВМ за времябыла отремонтирована (событиеА), а две исправные не вышли из строя (событиеВ). Тогда получим

Аналогично находим:

.

Рассуждая подобным образом, находим:

Составим матрицу переходов при и:

.

Для рассматриваемого примера система уравнений (53) может быть записана в следующем виде:

Решая полученную систему линейных уравнений с помощью одним из известных методов (например, методом последовательного исключения неизвестных) получим:

На этом мы закончим этот раздел и для читателей рекомендуем в целях более подробного ознакомления с этим важным разделом теории вероятностей обратиться к фундаментальным книгам [Гнеденко, Феллер и Карлин и др.].

В завершении этой тематики рассмотрим кратко понятие о непрерывном Марковском процессе и системы уравнения Колмогорова.