1. Случайная величина распределена нормально и ее среднее квадратическое отклонениеизвестно

8. Расчёт многоканальной смо с отказами методом Монте – Карло.

Пусть в систему массового обслуживания с отказами (заявка покидает такую систему, если все каналы заняты), состоящую из каналов, поступает простейший поток заявок (см. пример 5, пункт 2, Т.6), при этом плотность распределения промежутка времени между двумя последовательными заявками задана равенствами: при

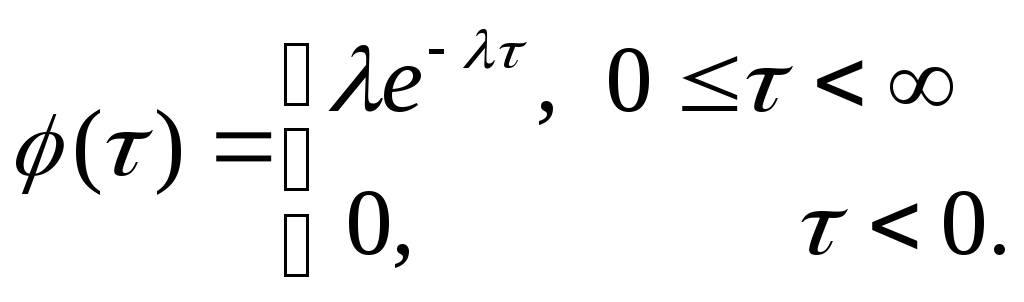
Каждая заявка поступает в первый канал. Если первый канал свободен, то он обслуживает поступившую заявку; если же первый канал занят, то заявка поступает во второй канал, и он обслуживает заявку (если канал в этот момент свободен) или заявка передаётся в третий канал (если первый и второй каналы заняты) и т.д.

В случае, если в момент поступления заявки все каналы заняты, наступает отказ и поступившая заявка не обслуживается и из дальнейшего рассмотрения исключается.

Ведётся подсчёт количества обслуженных заявок и количество отказов. Если заявка обслужена, то в «счётчик обслуженных заявок» добавляют единицу; при отказе единицу добавляют в «счётчик отказов».

Ставится задача:найти математические ожидания количества обслуженных заявок и количества отказов за фиксированный промежуток времени .

Решение.Для решения этой задачи производятиспытаний, каждое длительностью времении определяют в каждом испытании число «обслуженных» заявок и число «отказов».

Обозначим:

число испытаний;

обслуживания заявки каналом;

момент освобожденияго канал;

момент поступленияй заявки;

длительность времени между поступлениямий ий заявок;

момент поступленияй заявки;

Пусть первая заявка поступила в момент времени, т.е. когда все каналы свободны. Эта заявка поступит в первый канал и будет им обслужена за время за время. В счётчик обслуженных заявок надо записать единицу.

Моделируем (разыграем) момент, поступления второй заявки, для чего выбираем случайное числои разыграем(учитывая,распределено по показательному закону): по формуле

(см. Пункт 7. пример 2). Следовательно, вторая заявка поступит в момент времени

.

Если окажется, что (вторая заявка поступила после того, как первый канал освободился), то вторая заявка будет обслужена первым каналом и то первый канал занят, и заявка поступит во второй канал и будет им обслужена, и в счётчик обслуженных заявок надо добавить единицу.

Если же окажется, что то первый канал занят, и заявка поступит во второй канал и будет им обслужена, поскольку расчёт начат в предположении, что все каналы свободны; в счётчик обслуженных заявок надо добавить единицу. и в счётчик обслуженных заявок надо добавить единицу.

Дальнейший расчёт производится аналогично. Если в некоторой момент времени поступления очередной заявки все каналы заняты, то наступает отказ и в счётчик отказов надо добавить единицу.

Испытание заканчивается, если очередная заявка поступит в момент времени, превышающий момент окончания испытания, т.е. если наступит момент .

В итоге о испытания в счётчиках окажутся соответственно число обслуженных заявоки число отказов.

Пусть произведено всего испытаний, каждое с временным интервалом, причём вм испытании зарегистрированообслуженных заявок иотказов. В качестве оценок искомых математических ожиданий принимают соответственно выборочные средние:

.

Для вычисления наименьшего числа испытаний, которые с надёжностью заранее обеспечат заданную верхнюю границу ошибки(см. Т.19, формула (44)). Отсюда следует, что (см. замечание), гденаходят по формуле(см.Т.19, (47)), а

величина с.к.о для показательного распределения определяется равенством .

Пример 10. Предположим, что среднеквадратическое отклонениеи. Тогдаи, по таблице значений функции.

Следовательно, минимальное число испытаний равно

В наших рассмотрениях предполагалось, что время обслуживания - неслучайная величина; если время обслуживания случайно, то расчёт производится аналогично. Разумеется, для моделирования (разыгрывания) случайного времени обслуживания надо знать закон его распределения для каждого канала. На практике обычно расчёт производят на ЭВМ.