5. Смо с неограниченным ожиданием

и ограниченной длиной очереди

Пусть имеется n - канальная СМО с очередью, на которую не наложено ограничений ни по длине очереди, ни по времени ожидания. В силу неограниченности очереди каждая заявка рано или поздно будет обслужена, поэтому Для СМО с неограниченной очередью накладывается ограничениеЕслиэто условие нарушено, то очередь растет до бесконечности, наступает явление «взрыва». Вероятность простоя каналов равна

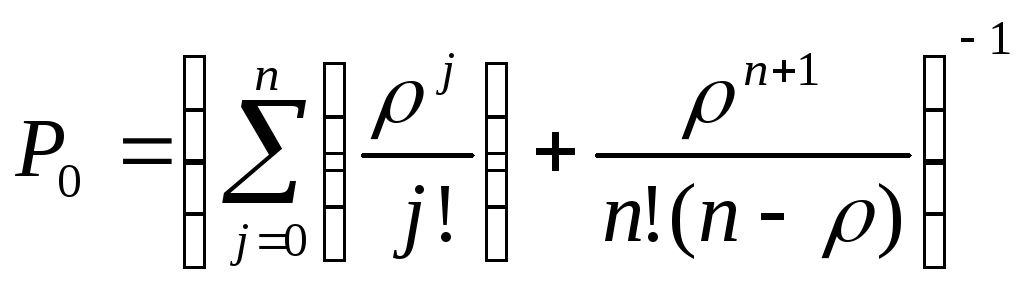
Вероятность занятости обслуживанием каналов равна

.

Вероятность занятости обслуживанием всех каналов при отсутствии очереди равна

Вероятность наличия очереди есть вероятность того, что число требований в системе больше числа каналов:

.

Вероятность попадания заявки в очередь есть вероятность за­нятости всех каналов. Эта вероятность равна сумме вероятностей наличия очереди и занятости всех п каналов при отсутствии очереди:

.

Среднее число занятых обслуживанием каналов равна

.

Доля каналов, занятых обслуживанием равна,

.

Среднее число заявок в очереди (длина очереди) равно

Среднее число заявок в системе равно

M = L+ T =L+p.

Среднее время ожидания заявки в очереди равно

.

Среднее время пребывания заявки в системе равно

Имеется n-канальная система с ожиданием, в которой количество заявок, стоящих в очереди, ограничено числом т, т.е. заявка, заставшая все каналы занятыми, становится в очередь, только если в ней находится менее т заявок. Если число заявок в очереди равно т, то последняя прибывшая заявка в очередь не становится и покидает систему необслуженной.

Системы с ограниченной очередью являются обобщением двух рассмотренных ранее СМО: при т = 0 получаем СМО с отказами, при получаем СМО с ожиданием.

Вероятность простоя каналов

Вероятность отказа в обслуживании равна вероятности того, что в очереди уже стоятт заявок:

Относительная пропускная способность есть величина, дополняющая вероятность отказа до 1, т.е. вероятность обслуживания

.

Абсолютная пропускная способность определяется равенством

,

Среднее число занятых каналов определяется равенством

,

Средняя длина очереди системы, т.е. среднее число заявок в очереди определяется равенством

.

Среднее время ожидания обслуживания в очереди равно

.

Среднее число заявок в СМО равно

M = L+ к.

Среднее время пребывания заявки в СМО равно

.

6. Замкнутые системы массового обслуживания

До сих пор мы рассматривали СМО, в которых входящий поток никак не связан с выходящим. Такие системы называются разомкнутыми. В некоторых же случаях требования, которые были обслужены, после задержки опять могут поступать на вход.

Такие системы массового обслуживания называются замкнутыми. Например, такие объекты, как, поликлиника, обслуживающая данную территорию, бригада рабочих, закрепленная за группой станков, являются примерами замкнутых систем. В замкнутой СМО циркулирует одно и то же конечное число потенциальных требований. Пока потенциальное требование не реализовалось в качестве требования на обслуживание, считается, что оно находится в блоке задержки. В момент реализации оно поступает в саму систему. Например, рабочие обслуживают группу станков. Каждый станок является потенциальным требованием, превращаясь в действующее в момент своей поломки. Пока станок работает, он находится в блоке задержки, а с момента поломки до момента окончания ремонта — в самой системе. Каждый рабо­чий является каналом обслуживания.

Пусть общее число каналов обслуживания, число потенциальных заявок, ,- интенсивность потока заявок каждого потенциального требования,интенсивность обслуживания. Тогда, в соответствии наших обозначений коэффициент загрузки системы равна Вероятность простоя системы определяется формулой

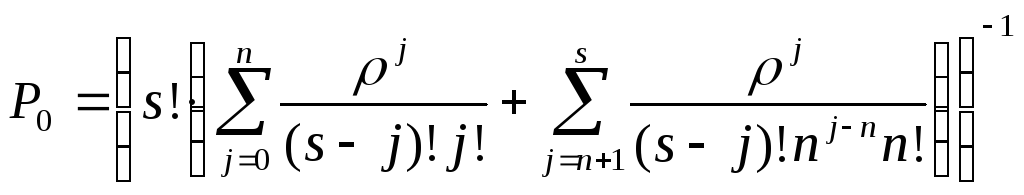
Финальные вероятности состояний системы определяются в виде:

Через эти вероятности выражается среднее число занятых каналов

Через находим абсолютную пропускную способность системы

А = ,

а также среднее число заявок в системе

.

Рассмотрим некоторые примеры.

Пример 3. На вход трехканальной СМО с отказами поступает поток заявок с интенсивностью равной 4 заявки в минуту, время обслуживания заявки одним каналом t_обсл = 1/μ = 0,5 мин. Выгодно ли с точки зрения пропускной способности СМО заставить все три канала обслуживать заявки сразу, при этом среднее время обслужи­вания уменьшается втрое? Как это скажется на среднем времени пребывания заявки в СМО?

Решение. Вероятность простоя трехканальной СМО согласно формуле равна

Вероятность отказа определяем по формуле вероятности отказа:

Относительная пропускная способность системы равна

Абсолютная пропускная способность системы равна

.

Среднее число занятых каналов 1,58, доля каналов, занятых обслуживанием равно,

Среднее время пребывания заявки в СМО находим как вероятность того, что заявка принимается к обслуживанию, умноженную на среднее время обслуживания: t 0,395 мин.

Объединяя все три канала в один, получаем одноканальную систему с параметрами μ = 6, = 2/3. Для одноканальной системы вероятность простоя равна

.

вероятность отказа равна

,

относительная пропускная способность равна

,

абсолютная пропускная способность равна

.

Среднее время пребывания заявки в СМО равно

.

В результате объединения каналов в один, пропускная способность системы снизилась, так как увеличилась вероятность отказа. Тем самым, среднее время пребывания заявки в системе уменьшилось.

Пример 4. На вход трехканальной СМО с неограниченной очередью поступает поток заявок с интенсивностью λ = 4 заявки в час, среднее время обслуживания одной заявки t= 1/μ 0,5 ч. Найти показатели эффективности работы системы.

Решение. Для рассматриваемой системы п = 3, λ= 4, μ = 1/0,5 = 2, =λ /μ = 2,

/n = 2/3 < 1. Определяем вероятность простоя системы:

.

Среднее число заявок в очереди находим по формуле:

.

Среднее время ожидания заявки в очереди определяется по формуле:

ч.

Среднее время пребывания заявки в системе равно

.

Пример 5. В парикмахерской работают 3 мастера, а в зале ожидания расположены 3 стула. Поток клиентов имеет интенсивность X = 12 клиентов в час. Среднее время обслуживания t ⁼ 20 мин. Определить относительную и абсолютную пропускную способ­ность системы, среднее число занятых кресел, среднюю длину очереди, среднее время, которое клиент проводит в парикмахерской.

Решение. Для данной задачи п = 3, т = 3, λ = 12, μ= 3, = 4,/п = 4/3.

Вероятность простоя равна:

.

Вероятность отказа в обслуживании определяем по формуле:

.

Относительная пропускная способность системы, т.е. вероятность обслуживания

.

Абсолютная пропускная способность

.

Среднее число занятых каналов

_.

Средняя длина очереди .

Среднее время ожидания обслуживания в очереди ч.

Среднее число заявок в СМО

.

Среднее время пребывания заявки в СМО

ч.

Пример 6. Рабочий обслуживает 4 станка. Каждый станок отказывает с интенсивностью λ = 0,5 отказа в час, среднее время ре­монта = 1/μ = 0,8 ч. Определить пропускную способность системы.

Решение. Эта задача рассматривает «замкнутую СМО», μ = 1,25, = 0,5/1,25 = 0,4. Вероятность простоя рабочего:

.

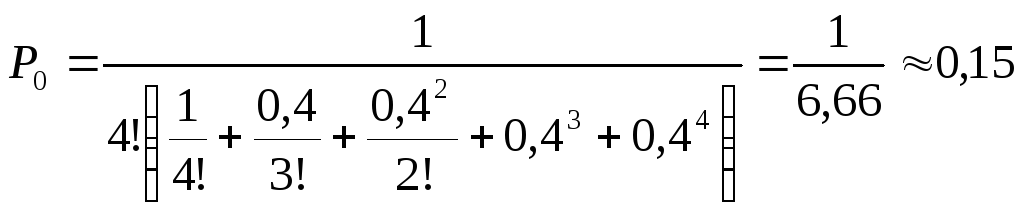Вероятность занятости рабочего P0,85. Если ра­бочий занят, он налаживает μ станков в единицу времени, пропускная способность системыстанков в час.

В заключении читателю рекомендуется обратиться к более обстоятельным учебникам, с целью получения углубленного знания по этому разделу [Карлин С.]