6. Интегральная функция распределения и связь с функцией плотности

Кратко рассмотрим, как между собой связаны функция плотности и функция распределения двумерной непрерывной случайной величины.

Зная дифференциальную функцию можно найти интегральную функцию по формуле (12)

,

что непосредственно следует из определения плотности распределения двумерной непрерывной с.в. (свойство 3).

Пример 7. Найти интегральную функцию распределения двумерной случайной величины по данной плотности распределения вероятности совместного распределения .

Решение. Воспользуемся формулой (9), с учётом имеем

Далее, найти вероятность попадания случайной точки в прямоугольник с вершинами K (1;1), L,M(1; 0) и N (; 0).

Решение. Искомая вероятность

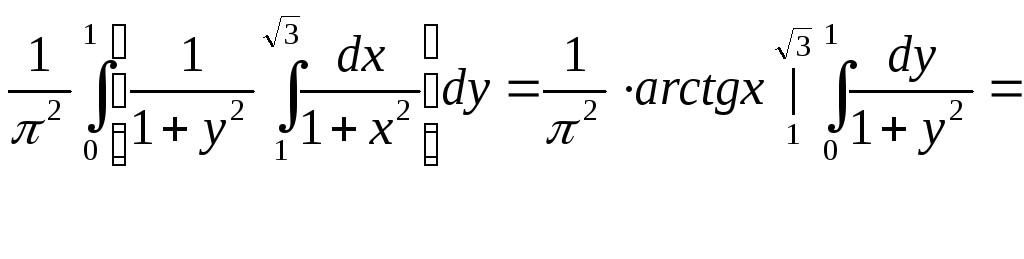
7. Зависимость и независимость двух случайных величин

Зная законы распределения двух с.в. и, входящих в системуможно найти закон распределения системылишь в случае, когда случайные величины иявляются независимы.

С понятием независимых случайных величин мы уже встречались неоднократно: две с.в. называются независимыми, если закон распределения каждой из них не зависит от того, какие значения принимает вторая с.в. В противном случае случайные величины называются зависимыми. Не приводя пока точных определений, рассмотрим несколько примеров. Они иллюстрируют разные степени зависимости между случайными величинами - от сильной почти функциональной зависимости до практической независимости.

- пусть рост наугад выбранного взрослого человека (в сантиметрах), аего вес (в килограммах). Зависимость между ростом и весом является весьма сильной, в начале её можно даже считать функциональной. Формула, приближённо выражающая эту зависимость, обычно пишется:

- пусть высота выбранного наугад дерева в лесу, адиаметр его основания. И здесь кажется зависимость сильной, хотя в реальности и в не такой степени, как в предыдущем примере.

- из груди камней нестандартной формы выбирают один камень. Пусть его масса, амаксимальная длина (скажем в диаметре). Зависимость между ними носит сугубо вероятностный характер.

- рост наугад выбранного взрослого человека (в сантиметрах), аего возрасть. Проведенные опыты показывают, что эти величины практически независимы.

Таким образом, степень зависимости между двумя с.в. могут быть как угодно и каким угодно.

Сформулируем общее определение независимости случайных величин с помощью событий: и.

Случайные величины иназываютсянезависимыми, если независимыми являются события: идля любых действительных чиселиВ противном случае с.в.иназываютсязависимыми.

Справедливо следующее условие независимости случайных величин.

Теорема 11.1. Для того, чтобы случайные величины ибыли независимы, необходимо и достаточно, функция распределения системыбыла равна произведению функций распределения её составляющих, т.е. выполнялось равенство:

(19) .

Доказательство. Пусть случайные величины инезависимы, тогда событияинезависимы. Отсюда следует, что, т.е. . Если же имеет место (16) , то

Значит с.в. инезависимы.

Сформулируем два утверждения относительно независимости двух случайных величин и(д.с.в. и н.с. в. соответственно), образующих систему.

Теорема 11.2. Необходимым и достаточным условием независимости двух дискретных случайных величин и, образующих систему, является равенство

(20) ,

для любых

На практике, как правило, легко проверять зависимость или независимость двух д.с.в.

Здесь ограничимся рассмотрением примера.

Пример 8. В двух ящиках находятся по шесть шаров; в 1-м ящике: один шар с номером 1, два шара с номером 2, три шара с номером 3. Во втором ящике: два шара с номером 1, три шара с номером 2, один шар с номером 3. Пусть номер шара, случайно вынутого из первого ящика,номер шара, случайно вынутого из второго ящика. Из каждого ящика вынули по одному шару. Составить таблицу закона распределения системы случайных величин.

Решение. Случайная точка (1;1) имеет кратность 12 =2;

Случайная точка (1;2) имеет кратность 13 =3;

Случайная точка (1;3) имеет кратность 11 =1;

Случайная точка (2;1) имеет кратность 22 =4;

Случайная точка (2;2) имеет кратность 23 =6;

Случайная точка (2;3) имеет кратность 21 =2;

Случайная точка (3;1) имеет кратность 32 =6;

Случайная точка (3;2) имеет кратность 33 =9;

Случайная точка (3;3) имеет кратность 31 =3;

Всего случайных точек 66=36 . Так как кратности точек отношение точки ко всему количеству точек равно вероятности появления этой точки, то таблица закона распределения системы с.в. имеет вид

X Y	1	2	3
1
2
3

Сумма всех вероятностей , указанных в таблице равна 1.(Проверьте!).

Случайные величины независимы. Поскольку выполняется равенство (17). Проще проверять по следующей таблице:

(21)

Отсюда легко видеть, что Таким образом,

Пример 9. В урне 4 шара: 2 белых, 1 чёрный, 1 синий. Из них наудачу извлекают два шара. Пусть с.в.число чёрных шаров в выборке, с.в.число синих шаров в выборке.

Составить закон распределения для системы Найти:

1) таблицу распределения системы ;

2) законы распределения и;

3) выяснить зависимость или независимость и.

Решение. Случайная величина с.в.. Вычислим соответствующие вероятности:

;

Следовательно, таблица распределения системы имеет вид

Y
0
1

Отсюда следует:

.

Законы распределения составляющих и

X	0	1	и	Y	0	1
p	0,5	0,5		p	0,5	0,5

Теорема 11. 3. Необходимым и достаточным условием независимости двух непрерывных случайных величин и, образующих систему, является равенство

(22)

Доказательство. Если инезависимые непрерывные случайные величины, то имеет место равенство (19).

Дифференцируя это равенство по , а затем по(с учётом равенства (9)), получим

,

Следовательно, необходимость равенство (22) получено. Покажем, что оно и достаточно.

Действительно, пусть выполняется равенство (22). Интегрируя по и по получаем

,

или . Достаточность доказана.

Пример 10. Двумерная случайная величина задана с плотностью распределения вероятностей . Найти:

1) - чтобы выполнялась условие нормированности;

2)

3)

4)

5) Убедитесь в выполнении условии нормировки для найденных функций:

и

1) Легко может быть показано, что величина , для этой цели следует проверить условие нормировки (см. равенство (13)):

.

Следовательно,

2) Используя свойство 3, (см. равенство (12)), находим

3)

4) По формуле (17) получаем

Аналогично, по формуле (18) получаем

.

Следовательно, . Поэтому на основании равенство (20) (теорема 11.2), заключаем, что случайные величиныинезависимы.

Теперь вернёмся к нашим примерам, рассмотренные в начале пункта (см. пример1).

Пример 11. Пусть наосновании некоторого опыта получены данные относительно человеческого роста и веса, которые представлены в виде следующей таблицы, и они могут быть описаны двумерной случайной величины, где обозначаетрост,вес.

X Y

В этой таблице обозначает вероятность того, что человек, обладающим ростом, обладает весом

Требуется найти одномерные законы распределения каждой из случайных величин системы .

Решение. Сложив вероятности по столбцам, получим вероятности возможных значений веса:

Закон распределения составляющей запишется так:распределение вероятности роста

Контроль: 0,26+ 0,38+0,36=1.

Закон распределения составляющей запишется так:распределение вероятности веса

Контроль: 0,56+ 0,44=1.

Пример 12. Система случайных величинхарактеризует рост и вес человека в отклонениях от средних значений: роствеси имеет функцию распределения

Найти плотность распределения вероятностей системы с.в.

Решение. На основании равенство (6) сначала берём частную производную поа затем пополучим:

Задания.

1. Найти функций плотностей одномерных распределений с.в.и.

Воспользуйтесь равенствами (14).

2. Система двух случайных величинподчинена равномерной плотности распределения внутри круга радиусомНаписать выражение для плотности распределения системы с.в.и отдельных случайных величини.

Указание.Воспользуйтесь равенством: