4. Линейная регрессия, прямые линии

среднеквадратической регрессии

Пусть двумерная случайная величина, гдеиявляются зависимые случайные величины. В этом пункте кратко рассмотрим приближённое представление одну из величин как линейную функцию через другой (точную функциональную зависимость, вообще говоря, описать невозможно!). Итак, пусть случайная величиначерез величиныприближенно представлена в виде, гдепараметры, подлежащие определению. Это можно сделать различными способами. Наиболее употребительными из них является «метод наименьших квадратов».

Функцию называют «наилучшим приближением» с.в.в смысле метода наименьших квадратов, если математическое ожиданиепринимает наименьшее возможное значение; функцию называют среднеквадратической регрессией с.в.на. Имеет место утверждение

Теорема 12.6. Линейная среднеквадратическая регрессия наимеет вид

(21) ,

где

коэффициент корреляции с.в. и.

Доказательство. Введём в рассмотрение функцию двух независимых аргументов

и:

(22)

На основании равенств:

и после выполнения некоторых выкладок (с учётом свойства м.о.) получим

Далее, исследуем функцию на экстремум. Для этого найдём частные производные и приравниваем нулю

Решая систему линейных уравнений относительно неизвестных иполучим:

.

Согласно общей теории функция при этих значениях ипринимает своё наименьшее значение (Убедитесь в этом!).

Итак, линейная средняя квадратическая регрессия иимеет вид

.

Утверждение доказано.

Коэффициент называют коэффициентом регрессиина, а прямую

(23)

называют прямой среднеквадратической регрессии на.

Подставляя найденные значения ив равенстве (23), получим минимальное значение функции, равноекоторую называютостаточной дисперсией с.в. относительно с.в.она характеризует величину ошибки, которую допускают при замене с.в.на линейной функцией. Приостаточная дисперсия равна нулю; т.е. при этих крайних значениях коэффициента корреляции не возникает ошибки при заменев виде линейной функции отСледовательно, еслитоимежду собой связаны линейной функциональной зависимостью.

Аналогично, можно получить прямую линию среднеквадратичной регрессии с.в.на:

(24)

(коэффициент регрессиина), а также остаточную дисперсиювеличиныотносительно.

Если , то обе прямые регрессии, как видно из (23) и (24) совпадают.

Из уравнений (23) и (24) вытекает, что обе прямые регрессии проходят через точку, которую называютцентром совместного распределения величин и.

Важной характеристикой условного распределения вероятностей является условное математическое ожидание.

5. Условное математическое ожидание, линейная

корреляция, теорема о нормальной корреляции

При изучении двумерной случайной величины рассматриваются не только числовые характеристики одномерных компонент и, но и числовые характеристики условных распределений: условные м.о. и условные дисперсии.

Условным математическим ожиданием одной из случайной величины, входящих в систему называется её м.о., вычисляемое при условии, что другая с.в. приняла определенное значение (или попала в данный интервал). Обозначается: иилии.вычисляются соответственно (для д.с.в. и для н.с.в.) по формулам:

(25)

где – условная вероятностная плотность случайной величины при . Отметим, что условное математическое ожиданиеесть функция от:, называют функциейрегрессиис.в.на.

Аналогично определяется условное математическое ожидание случайной величины

(26)

и функция регрессии на:.

Графики этих функций называются соответственно линиями (или «кривыми») регрессии с.в.наи с.в.на. Рассмотрим пример для случая д.с.в.

Пример 6. Дискретная двумерная случайная величина задана таблицей

	1	3	4	8
3
6

Найти условное математическое ожидание составляющей при

Решение.Найдем, для этого сложим вероятности, помещенные в первом столбце таблицы.

Найдем условное распределение вероятностей величины при

Вычислим искомое условное математическое ожидание по первой формуле (34):

.

Задание. а) Вычислите величины:;

б) Вычислите величины:

Теперь рассмотрим важный случай, когда обе функции регрессии наиналинейны. В этом случае говорят, что с.в.исвязанылинейной корреляционной зависимостью.

Теорема 12.7. (Теорема о нормальной корреляции). Если двумерная случайная величина распределена по нормальному закону, то с.в.исвязаны линейной корреляционной зависимостью.

Доказательство.Найдём условное м.о.(т.е. функция регрессиина), используя условный закон распределения с.в.прикоторый определяется условной плотностью распределенияНа основании формулы (23) п.13.5

Совместная плотностьзадана формулой (40), а плотность распределения составляющейравна (см.формулу(42))

.

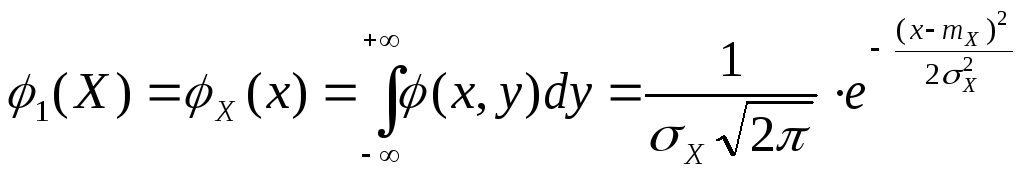Поэтому, имеем

.

Произведём упрощения в экспоненте последней формулы, получим

Следовательно,

(27) .

Отсюда легко заметить, что условный закон распределения является нормальным с условным математическим ожиданием и условной дисперсией, определяемыми равенствами:

(28) и

Аналогично

(29) и

Так как обе функции регрессии (28 и (29) линейны, то корреляция между с.в.илинейная. Утверждение доказано.

Задача. Пустьдвумерная нормальная случайная величина с параметрамиНайти условную плотность распределения с.в.при условии,и с.в.при условии,.

Указание. Воспользоваться формулами (16) и (17).

Рассмотрим пример, когда система с.в. подчинена линейному закону распределения.

Пример 7. Система случайных величинподчинена закону распределения с функцией плотностью

Областьквадрат, ограниченный прямыми линиями:

Требуется:

1) Определить коэффициент

2) вычислить вероятность попадания случайной точки в квадратограниченный прямыми линиями:

3) найти математические ожидания и

4) найти средние квадратичные отклонения

Решение. 1) Коэффициентнаходим из интегрального уравнения (контроль):

.

Вычислим интеграл

Следовательно,

2)

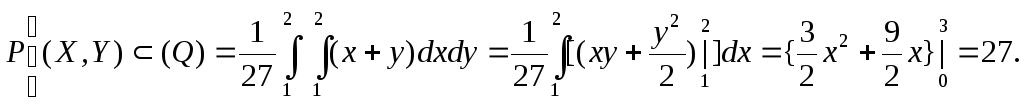
3) Находим математические ожидания иимеем

Аналогично, находится и

4) Находим среднеквадратичные отклонения и: имеем

Задание.

1. Найти в примере 7, ковариациюсистемы случайных величини коэффициент корреляции.

2. Найти законы распределения составляющих дискретной двумерной случайной величины, заданной законом распределения

X Y

Ответ. ,

.

3. Найти вероятность того, что составляющая X двумерной случайной величины примет значение и при этом составляющаяY примет значение , если известна, что интегральная функция системы

Отв.

4. Найти вероятность попадания случайной точки (X, Y) в прямоугольник, ограниченный прямыми: если известна интегральная функция

Отв.

5. Найти дифференциальную функцию системы двух случайных величин по известной интегральной функции

Отв.

6.Системы двух с.в.подчинена равенствами:

Область (D), определяется неравенствами:

Найти:

1) определить коэффициент .

2)

3) математические ожидания и;

4) средние квадратичные отклонения и

5) ковариацию системы случайных величини коэффициент корреляции.

Отв. 1) 2);

3) =.

4)

7. Система двух случайных величин распределена равномерно: в прямоугольнике , ограниченном прямыми линиями: дифференциальная функция сохраняет постоянное значение, а вне этого прямоугольника она равна нулю.

Найти: а)дифференциальную функцию, б) интегральную функцию системы

Ответы. a)

8.Пусть дифференциальная функция системы двух случайных величин имеет вид

Найти: а) величину C, б) интегральную функцию системы

9. Двумерная случайная величина задана дифференциальной функцией

Найти условные законы распределения составляющих

10. Система с.в.подчинена закону распределения с плотностью

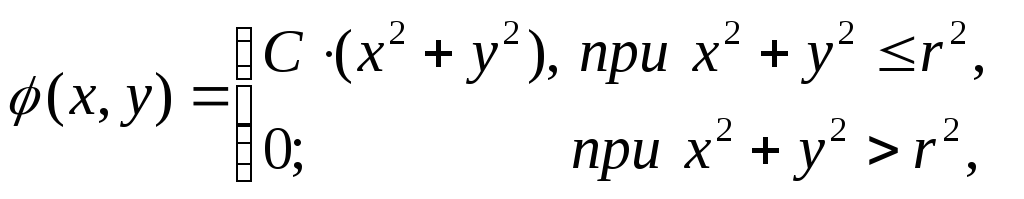
Найти: а) коэффициент . б)?

Указание. Коэффициентследует определить из равенства (контроль)

где круг, ограниченный окружностьюПереходите к полярным координатам, тогда

Функцию совместного распределения нужно определить из (12) (см. Т.11.,п.11.6).