4. Центральная предельная теорема

Центральная предельная теорема (ЦПТ) представляет собой вторую группу предельных теорем, которые устанавливают связь между законом распределения суммы случайных величин и его предельной формой –нормальным законом распределения.

До сих пор мы часто говорили об устойчивости средних характеристик большого числа испытаний, говоря точнее, об устойчивости сумм вида

Однако следует обратить внимание, что величинаслучайная, а значить, она имеет некоторый закон распределения. Оказывается этот замечательный факт, составляет содержание

другой группы теорем, объединяемых под общим названием центральная предельнаятеорема, что при досточно общих условиях закон распределенияблизок к нормальному закону.

Поскольку величина отличается от суммы

лишь постоянным множителем то в общих чертах содержание ЦПТ может быть сформулировано следующим образом.

Распределение суммы большого числа независимых случайных величин при весьма

общих условиях близко к нормальному закону распределению.

Известно, что нормально распределенные случайные величины широко распространены на практике (не только в теории вероятностей, но и в её многочисленных приложениях). Чем такое явление объясняется? Ответ на такой «феномен» впервые был дан выдающимся русским математиком А.М. Ляпуновым в 1901году: «Центральная предельная теорема Ляпунова». Ответ Ляпунова заключается в его условии, при которых справедливо ЦПТ (см. далее).

В целях подготовки точной формулировки ЦПТ, поставим перед собой два вопроса:

1. Какой точный смысл содержит в себе утверждение о том, что «закон распределения суммы «близка» к нормальному закону?».

2. При каких условиях справедлива эта близость?

Чтобы ответить на эти вопросы, рассмотрим бесконечную последовательность случайных величин: Составим «частичные суммы» нашей последовательности с.в.

(23)

От каждой случайных величин перейдём к «нормированной» случайной величине

(24)

Нами было установлено (см.Т.8., п.3, равенства (19)), что .

Ответ на первый вопрос теперь можно сформулировать в виду предельного равенства

(25) , (,

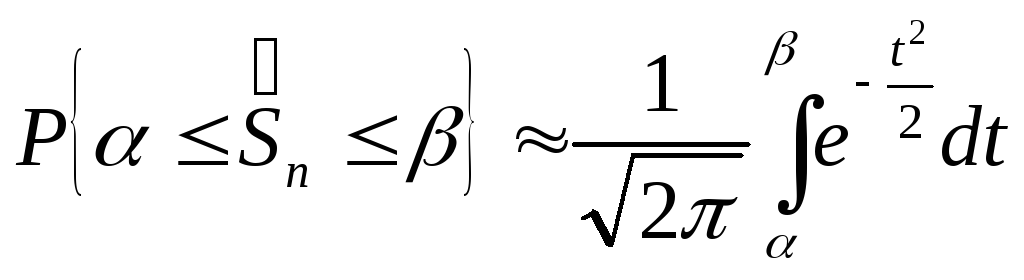означающего, что закон распределения с.в. с ростомприближается к нормальному закону с. Разумеется, из того факта, что величинаимеет приближенно нормальное распределение, следует, что и величинараспределена приближенно нормально,

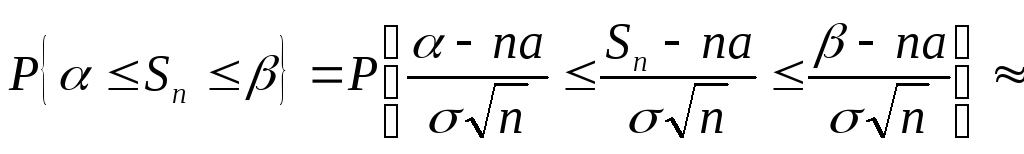
или

(26)

- формула для определения вероятности того, что сумма нескольких с.в. окажется в заданных пределах. Часто ЦПТ используют при

По поводу условий, которые следует наложить на величины можно высказать следующие соображения. Рассмотрим разностьПолучим отклонение с.вот её математического ожидания. Общий смысл накладываемых условий, на величинызаключается в том, что отдельные отклонениядолжны быть равномерно малы по сравнению с суммарным отклонениемТочную формулировку этих условий, при которых справедливо предельное соотношение дал М.А. Ляпунов в 1901 году. Она заключается в следующем.

Пусть для каждой из величин числаконечны, (заметим, чтоесть дисперсия с.в.- «центральный момент третьего порядка»).

Если при

,

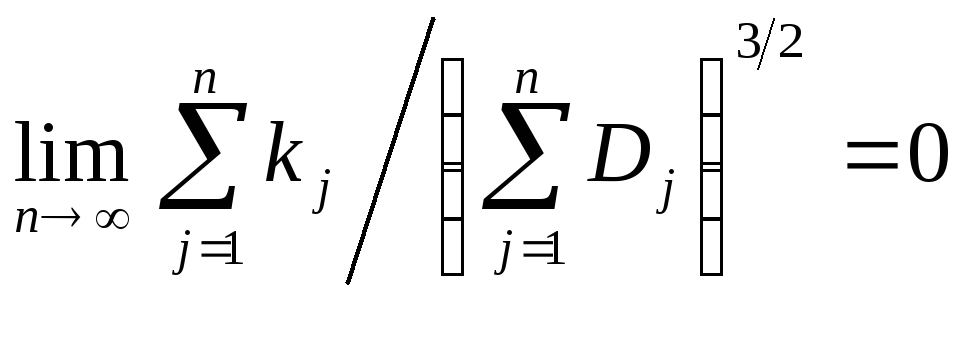то будем говорить, что последовательность удовлетворяетусловию Ляпунова.

В частности, ЦПТ для случаев, когда в сумме случайных величин каждый слагаемый имеет одинаковое распределение, т.е. все ито условие Ляпунова выполняется

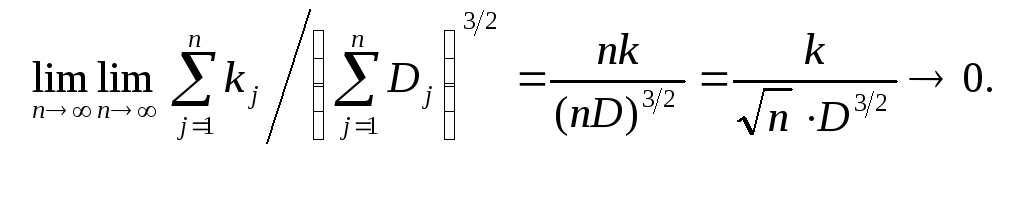
Именно, на практике такой случай ЦПТ чаще всего используется. Потому, что в математической статистике любая случайная выборка с.в. имеют одинаковые распределения, поскольку «выборки» получены из одной и той же генеральной совокупности.

Сформулируем этот случай как отдельное утверждение ЦПТ.

Теорема 10.7 (ЦПТ). Пусть случайные величины независимы, одинаковораспределены, имеют конечные математическое ожидание и дисперсию

Тогда функция распределения центрированной и нормированной суммы этих с.в. при стремится к функции распределения стандартной нормальной случайной величины:

(27)

где

На этом частном случае хорошо осмыслить, в чем находит своё проявление равномерная «малость» слагаемых, где величинаимеет порядок, а величинапорядок, тем самым отношение первой величины ко второй стремится, к 0.

Теперь мы в состоянии сформулировать центральную предельную теорему в форме А.М. Ляпунова.

Теорема 10.8. (Ляпунова). Если последовательность независимых случайных величин удовлетворяет условию Ляпунова, то справедливо предельное соотношение

(28) ,

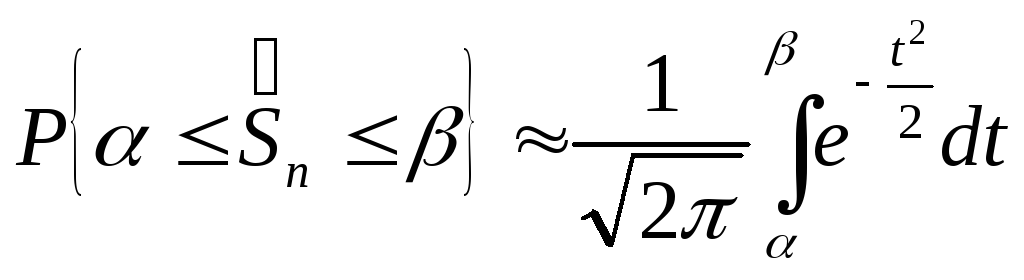для любых и, при этом (.

Иными словами, в этом случае закон распределения нормированной суммы сходится к нормальному закону с параметрами

Следует отметить, что для доказательства ЦПТ А.М. Ляпунов разработал специальный метод, основанный на теорию так называемых характеристических функций. Этот метод оказался весьма полезным и в других разделах математики (см. доказательство ЦПТ например в кн. Бородин […] ). В этой книге мы, о производящих функциях будем давать краткую информацию и некоторые применения к подсчёту числовых характеристик случайных величин.

Краткие сведения об ошибке измерений. Известно, что при повторении измерений одного и того же объекта, выполненными одним и тем же измерительным прибором с одинаковой тщательностью (при одинаковых условиях) не всегда достигаются одинаковые результаты. Разброс результатов измерения вызван тем, что на процесс измерения влияют многочисленные факторы, которые не возможно и не целесообразно учитывать. В этой ситуации ошибку, возникающую при измерении интересующей нас величины часто можно рассматривать как сумму большого числа независимых между собой слагаемых, каждое из которых даёт лишь незначительный вклад в образование всей суммы. Но такие случаи приводят нас как раз к условиям применимости теоремы Ляпунова и можно ожидать, что распределение ошибки измеряемой величины мало отличается от нормального распределения.

В более общем случае, ошибка является функцией большого числа случайных аргументов, каждый из которых лишь немного отличается от своего математического ожидания. Линеаризуя эту функцию, то есть, заменяя её линейной, опять приходят к предыдущему случаю. Накопленный опыт по статистической обработке результатов измерений действительно подтверждает этот факт в большинстве практических случаев.

Аналогичные рассуждения объясняют появление нормального распределения в отклонениях параметров, определяющих выпущенную готовую продукцию (изделия), от нормативных значений при массовом производстве.

Рассмотрим следующий пример.

Пример 5. Независимые случайные величиныраспределены равномерно на отрезке [0,1]. Найти закон распределения с.в., а также вероятность того, что

Решение.Условия ЦПТ соблюдается, поэтому с.в.имеет приближенно плотность распределения

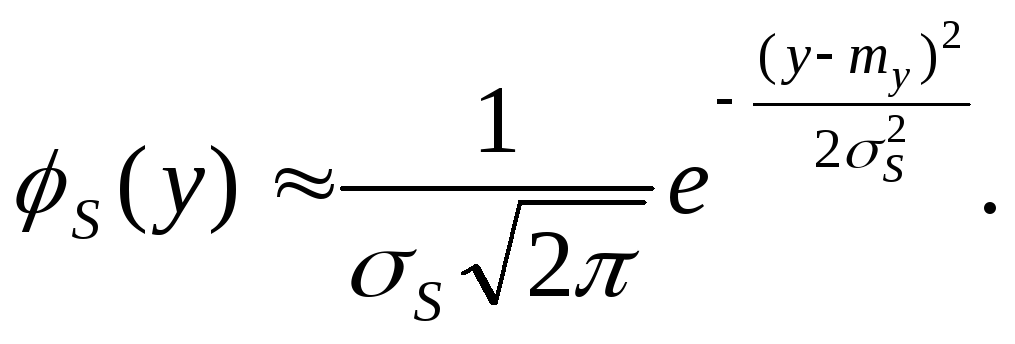
По известным формулам для м.о. и дисперсии в случае равномерного распределения находим: Тогда

.

Поэтому

На основании формулы (26), находим (с учётом табличных значений функции Лапласа)