
- •Тема 13. Многомерная случайная величина (общие сведения)
- •1. Многомерная случайная величина
- •2. Характеристическая функция и её свойства
- •3. Примеры вычисления характеристических функций
- •3.1. Характеристическая функция биномиального закона.
- •3.2. Характеристическая функция закона Пуассона.
- •3.3. Характеристическая функция геометрического закона.
- •Тема14. Функции случайных величин
- •1. Функция одного случайного аргумента
- •2. Функция двух случайных аргументов
- •Тема 15. Распределение функций нормальных
- •2. Распределение Стьюдента
- •3. Распределение Фишера – Снедекора (распределение)
Тема 15. Распределение функций нормальных
случайных величин
Рассмотрим распределение некоторых случайных величин, представленные функцией нормально распределённых с.в., часто используемые в математической статистике.
1. Распределение
«![]() хи-квадрат или
хи-квадрат или
распределения Пирсона»
Пусть
![]() независимые случайные величины,
распределённые по нормальному закону,
при этом предполагается, что математическое
ожидание и дисперсия каждого из них
равны:
независимые случайные величины,
распределённые по нормальному закону,
при этом предполагается, что математическое
ожидание и дисперсия каждого из них
равны:![]()
![]() .
.
Распределением
![]() с
с![]() степенями свободы называется
распределение суммы
степенями свободы называется
распределение суммы
![]()
Плотность вероятности с.в.![]() зависит только от числа слагаемых
зависит только от числа слагаемых![]() .
Например, если
.
Например, если![]() ,
то
,
то![]() где
где![]() а плотность распределения равна
а плотность распределения равна
![]()
Плотность вероятности с.в.![]() при
при![]() определяется равенствами
определяется равенствами
(1)

где
![]() гамма
- функция Эйлера,
гамма
- функция Эйлера,![]() ,
в частности,
,
в частности,![]()
С возрастанием числа
![]() -
степени свободы распределение
-
степени свободы распределение![]() приближается
к нормальному закону распределения
(при
приближается
к нормальному закону распределения
(при![]() распределение
распределение![]() практически
не отличается от нормального распределения),
причём выполняются равенства:
практически
не отличается от нормального распределения),
причём выполняются равенства:
(2)
![]()
На практике, как правило, используют
не плотность вероятности, а квантили
(Т.8.) распределения
![]() .
.
Квантилю распределения![]() ,
соответствующей уровню значимости
,
соответствующей уровню значимости![]() ,
называется такое значение,
,
называется такое значение,![]() при
котором выполняется равенство
при
котором выполняется равенство
(3)
![]() .
.
С геометрической точки зрения нахождение
квантили
![]() заключается
в выборе такого значения
заключается
в выборе такого значения![]() ,
чтобы площадь заштрихованной области
на рис.56 фигуры была равна
,
чтобы площадь заштрихованной области
на рис.56 фигуры была равна![]() .
.
x
Рис. 56 стр 159 Письмен…
Значения квантилей приводятся в специальных таблицах- приложениях (Письмен…стр.286, приложение 3.).
Для стандартного нормального распределения
квантили уровня
![]() обозначаются через
обозначаются через![]() при этом
при этом![]() является
решением интегрального уравнения
является
решением интегрального уравнения
(4)
![]()
Следует заметить, что распределение![]() определяется
одним параметром – числом степеней
свободы
определяется
одним параметром – числом степеней
свободы![]() и с увеличением числа степеней свободы
распределение медленно приближается
к нормальному закону. Распределение
и с увеличением числа степеней свободы
распределение медленно приближается
к нормальному закону. Распределение![]() так
же называют критерием согласия
так
же называют критерием согласия![]() Пирсона[с.м.книгу ТВ.и МС.
А. А. Белов, Баллод, …]. Оно позволяет
проверить статистических гипотез о
распределении вероятностей случайной
величины.
Пирсона[с.м.книгу ТВ.и МС.
А. А. Белов, Баллод, …]. Оно позволяет
проверить статистических гипотез о
распределении вероятностей случайной
величины.
2. Распределение Стьюдента
Пусть
![]() -
стандартная нормальная случайная
величина, независящая от
-
стандартная нормальная случайная
величина, независящая от![]() распределения,
а
распределения,
а![]() независимая
от
независимая
от![]() случайная
величина, распределённая по закону
случайная
величина, распределённая по закону![]()
Распределением Стьюдента (или
![]() распределением)
с
распределением)
с
![]() степенями свободы называется распределение
случайной величины
степенями свободы называется распределение
случайной величины
(5)
![]() .
.
«Стьюдент-псевдоним английского статистика В. Госсета».
Плотность вероятности Стьюдента имеет вид
(6)

При
![]() распределение Стьюдента приближается
(начиная уже с
распределение Стьюдента приближается
(начиная уже с![]() почти
совпадает) к нормальному закону с
математическим ожиданием и дисперсией:
почти
совпадает) к нормальному закону с
математическим ожиданием и дисперсией:
(7)
![]() .
.
На практике используют квантили
![]() распределения.
Это такое значение
распределения.
Это такое значение![]() что
что
(8)
![]()
С геометрической точки зрения задача
нахождение квантилей заключается в
выборе такого значения
![]() ,
чтобы площадь заштрихованной фигуры
на рис. 57 была равна
,
чтобы площадь заштрихованной фигуры
на рис. 57 была равна![]()
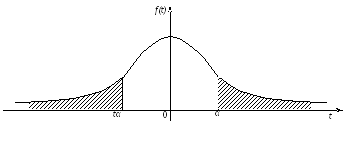 Рис.57,
сир 160.
Рис.57,
сир 160.![]()
Мы ещё вернёмся к этому распределению в разделе Математической статистики …
