
- •Тема 13. Многомерная случайная величина (общие сведения)
- •1. Многомерная случайная величина
- •2. Характеристическая функция и её свойства
- •3. Примеры вычисления характеристических функций
- •3.1. Характеристическая функция биномиального закона.
- •3.2. Характеристическая функция закона Пуассона.
- •3.3. Характеристическая функция геометрического закона.
- •Тема14. Функции случайных величин
- •1. Функция одного случайного аргумента
- •2. Функция двух случайных аргументов
- •Тема 15. Распределение функций нормальных
- •2. Распределение Стьюдента
- •3. Распределение Фишера – Снедекора (распределение)
2. Функция двух случайных аргументов
При рассмотрении данного раздела в основном будем следовать книге [Письм. гл.4].
Для успешного решения ряда практических
задач нужно знать закон распределения
(или числовые характеристики) следующих
случайных величин:![]()
![]()
![]()
![]() и
других.
и
других.
Приведём общее определение функции для двух случайных величин.
Каждой паре с.в.
![]() ;
;![]() по заданному правилу
по заданному правилу![]() ,
ставим в соответствие вполне определённое
значение с.в.
,
ставим в соответствие вполне определённое
значение с.в.![]() то
то![]() называется функциейдвух случайных
аргументов
называется функциейдвух случайных
аргументов ![]() и
и![]() ,
и обозначают в виде:
,
и обозначают в виде:![]() .
.
Рассмотрим закон распределения с.в.
![]() ,
наиболее часто встречающийся на практике.
Пусть система двух непрерывных с.в.
,
наиболее часто встречающийся на практике.
Пусть система двух непрерывных с.в.![]() имеет совместную плотность распределения
имеет совместную плотность распределения![]() .
Тогда в соответствии со свойствами
плотности двумерной с.в.
.
Тогда в соответствии со свойствами
плотности двумерной с.в.![]()
(см.11.6. равенство (11)) найдём функцию
распределения с.в.
![]() .
.
![]() .
.
Здесь
![]() множество
точек плоскости
множество
точек плоскости![]() ,
координаты которых удовлетворяют
неравенству
,
координаты которых удовлетворяют
неравенству
![]() (см.47.)
(см.47.)

Рис. 47.(Письм)
Следовательно, имеем
![]() .
.
Дифференцируя полученное равенство по
переменной
![]() ,
входящей в верхний предел внутреннего
интеграла, получаем выражение для
плотности распределения с.в.
,
входящей в верхний предел внутреннего
интеграла, получаем выражение для
плотности распределения с.в.![]() :
:
![]() (6)
(6)![]() .
.![]()
Если с.в.
![]() и
и![]() являютсянезависимыми, то согласно равенству
являютсянезависимыми, то согласно равенству![]() ,
то из (6) получим
,
то из (6) получим
![]() (7)
(7)![]() .
.![]()
Закон распределения суммы независимых
с.в. называется композициейилисвёрткойзаконов распределения
слагаемых. Для них принято специальное
обозначение:
![]() ,
,
где
![]() знак
свёртки, а формул (7) называют формулой
свёртки или формулой композиции двух
распределений. В равенстве (6) записав
знак
свёртки, а формул (7) называют формулой
свёртки или формулой композиции двух
распределений. В равенстве (6) записав![]() в
виде
в
виде![]() ,
можно получить и другое представление
для
,
можно получить и другое представление
для![]() ,
а именно
,
а именно
![]() ,
,
и для
независимых случайных величин
![]() и
и![]() формулу
(7) можно переписать в виде
формулу
(7) можно переписать в виде
(8)
![]() .
.
Аналогично решаются задачи нахождения
законов распределения с.в.
![]() и других. Рассмотрим некоторые примеры.
и других. Рассмотрим некоторые примеры.
Пример 4. Независимые с.в.![]() и
и![]() распределены
равномерно
распределены
равномерно![]() и
и![]() .
Найти плотность распределения вероятностей
с.в.
.
Найти плотность распределения вероятностей
с.в.![]() (рис.
50)
(рис.
50)

Рис.50
Решение.![]() По условию
система случайных
величин
По условию
система случайных
величин
![]() равномерно распределена
в прямоугольнике
равномерно распределена
в прямоугольнике
![]() ,
следовательно,
,
следовательно,


По условию с.в.![]() и
и![]() являются
независимыми, то
являются
независимыми, то![]() ,
и
,
и
![]()
где
![]() площадь
области
площадь
области![]() части
прямоугольника, лежащей ниже прямой
части
прямоугольника, лежащей ниже прямой![]() :
т.е.
:
т.е.
1. если
![]() то
то![]()
2. если
![]() ,
то
,
то![]() (так
как
(так
как![]() );
);
3. если
![]() ,
то
,
то![]()
4. если
![]() ,
то
,
то![]()
5. если
![]() ,
то
,
то![]() .
.
Итак,

Проверим контроль:
![]() .
.
Полученную плотность
распределения
![]() можно найти другим способом, используя
формулу (7), т.е. на основании равенства
можно найти другим способом, используя
формулу (7), т.е. на основании равенства
![]() .
.
Имеем
![]() .
.
Функция под знаком интеграла отлична от нуля лишь в случаях
(9)
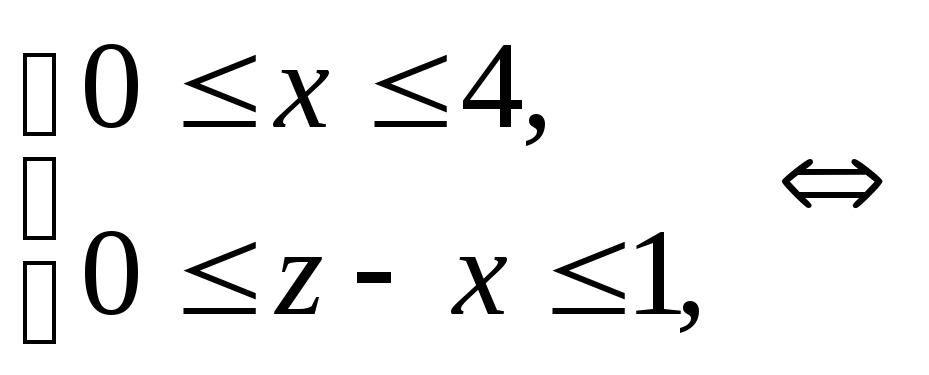

Решение системы зависит от значения
![]() .
.
1. Если
![]() то
система не имеет решений, так как отрезки
то
система не имеет решений, так как отрезки![]() и
и![]() не пересекаются. Следовательно,
не пересекаются. Следовательно,![]() и
и![]()
2. Если
![]() то
система (9) эквивалентна неравенству
то
система (9) эквивалентна неравенству![]() ,
поэтому
,
поэтому
![]()
3. Если
![]() то
система (9) эквивалентна неравенству
то
система (9) эквивалентна неравенству![]() ,
поэтому
,
поэтому
![]()
4. Если
![]() то
система (9) эквивалентна неравенству
то
система (9) эквивалентна неравенству![]() ,
поэтому
,
поэтому
![]()
5. Если
![]() то
система (9) не имеет решений, поэтому
то
система (9) не имеет решений, поэтому![]()
Таким образом, на основании 1.-5. получим

Задание. Изобразите
на отрезках прямых линий (на разных
параллельных линиях) интервалы изменения
переменных
![]() и
и![]() заштриховывая
их в каждом из пяти случае.
заштриховывая
их в каждом из пяти случае.
Пример 5. Совместное
распределение с.в.
![]() и
и![]() задано
плотностью распределения вероятностей
задано
плотностью распределения вероятностей
(10)

Найти функцию распределения
и с помощью дифференцирования плотность
распределения вероятностей с.в.
![]() .
.
Решение. Сначала
найдём функцию распределения
![]() с.в.
с.в.![]() ,
а затем вычислим её производную
,
а затем вычислим её производную![]() .
В соответствии с формулой (11) пункта
11.6 имеем
.
В соответствии с формулой (11) пункта
11.6 имеем
![]()
где![]() выражает множество точек, координаты
которых удовлетворяют неравенству
выражает множество точек, координаты
которых удовлетворяют неравенству![]() ,
,
т.е.
![]() (эти точки находятся выше прямой
(эти точки находятся выше прямой![]() ),
где
),
где![]() произвольное
число. Ясно, что если
произвольное
число. Ясно, что если![]() ,
то
,
то![]() ;
так как по условию примера вне единичного
квадрата
;
так как по условию примера вне единичного
квадрата![]() .
.
Область
интегрирования ![]() при
при![]() изображена на рис. 48, при
изображена на рис. 48, при![]() на
рис. 49.
на
рис. 49.


Рис. 48 ; рис.49.(Письменный)
При
![]() имеем
имеем

![]()
![]()
![]()
![]()
При
![]() имеем
имеем
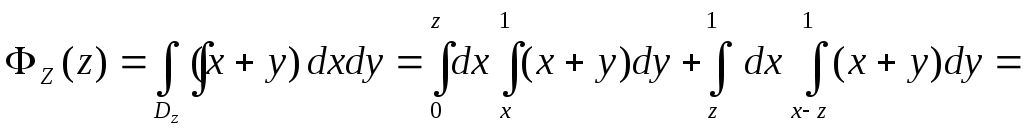
![]()
![]()
![]()
После стандартных подсчётов и упрощений окончательно получим
![]()
Остаётся
случай
![]() ,
имеем
,
имеем

![]()
Таким образом, для функции распределения
с.в.
![]() получим
получим

Следовательно,

Проверим контроль.
![]()
Упражнение. На основании условии (10) примера 5 найти функции и плотности распределения вероятностей случайных величин:
1.
![]() ,2.
,2.
![]() .
.
Пример 6.
Пусть
![]() и
и![]() независимые случайные величины, при
этом
независимые случайные величины, при
этом![]() и
и![]() .
Найти закон распределения с.в.
.
Найти закон распределения с.в.![]() .
.
Решение. На основании формулы (7) получим
![]()

На
основании интеграла Пуассона
![]() получим
получим

Следовательно, сумма
![]() двух
независимых нормальных с.в.
двух
независимых нормальных с.в.![]() и
и![]() c
числовыми характеристиками:
c
числовыми характеристиками:![]()
![]() имеет
нормальное распределение с математическим
ожиданием
имеет
нормальное распределение с математическим
ожиданием![]()
