Тема14. Функции случайных величин

Часто возникают задачи, в которых по известному закону распределения (или числовым характеристикам) одной (или нескольких) случайной величины требуется определить распределение другой (или нескольких) с.в., функционально связанные между собой.

1. Функция одного случайного аргумента

Если каждому возможному значению с.в. по определённому правилу соответствует одно возможное значение с.в.тоназывают функцией случайного аргументазаписывают

Пусть д.с.в. с возможными значениямис соответствующими вероятностями,Очевидно, что с.в.является также д.с.в. с возможными значениямивероятности которых равны соответственно

Отметим, что различным значениям с.в. могут соответствовать одинаковые значения с.в.В этом случае вероятности повторяющихся значений нужно складывать и это число будет вероятностью этой повторяющееся значения случайной величины.

Математическое ожидание и дисперсия функции определяется соответственно равенствами:

Пример 1.Задан закон распределения д.с.в.:

	-1	1	2
	0, 1	0,3	0,6

Найти если: 1)2)

Решение. 1) Перечислим значения с.в.; Отсюда получим соответствующие вероятности=0,6.

Найдём закон распределения функции :

Следовательно,

Для сравнения найдём

2) Найдём закон распределения

	8	12	14
	0, 1	0,3	0,6

Следовательно,

Задание. Найти

Пусть непрерывная с.в. с плотностью распределения, а с.в.есть функция от с.в.Найдём закон распределения с.в..

Для дальнейшего будем считать функцию непрерывной, строго возрастающей и дифференцируемой в интервале(отрезок может быть вся числовая прямая) всех возможных значений с.в.

Тогда существует функция обратная к функции(случайная точкалежит на графике кривой).

Определим функцию распределения с.в. . Или можно пользоваться и другими обозначениями:.

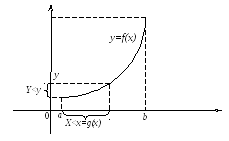
(Рис. 46 из Письм. В графике нужно заменить на),

Поскольку событие эквивалентно событию, то

т.е.

.

Дифференцируя это равенство по , найдём плотность распределения с.в.:

т.е.

(1) .

Если функция в интервалестрого убывает, то событиеэквивалентно событию. Поэтому

.

Отсюда следует, что

(2)

Учитывая, что плотность распределения не может быть отрицательной, формулы (1) и (2) можно объединить в одну

(3)

Эта формула верна и для взаимно однозначных (для них существует обратная функция) кусочно монотонных функций Тот факт, что для счётного числа точек (концов интервалов монотонности) формулой (3) значение функции плотности не определяются, не является принципиальным. Плотности на выделенном счётном множестве можно придать любое значение, при этом функция распределения не изменится в силу свойства интеграла.

Пример 2. Найти плотность распределения функции при условии, что с.в.имеет плотность

Решение. Функция монотонно убывает в интервалеОбратная функция есть

На основании формулы (3)получим:

Покажем на этом примере как выводится формула для плотности и функции распределения с.в.

Далее вычислим функцию плотности с.в. . Имеем по определению

,

Следовательно,

Замечание. Если функция немонотонна в интервале, то для нахождения функции плотности с.в.следует разбить интервал научастков монотонности, затем найти обратную функцию на каждом из них и воспользоваться формулой

(4)

Существует широкий класс функций не объязательно монотонных, для которыхбудет случайной величиной. К нему относятся, например, все непрерывные функции.

Если с.в. является непрерывной ии ё плотность распределения, то для нахождения числовых характеристик с.в.необязательно находить закон её распределения, можно воспользоваться формулами:

(5) .

Обсуждение общей проблемы выходит за рамки нашей книги (В общем случае к этим вопросам довольно плодотворно применяется теория суммируемых функций и интегралов Стилтьеса), и мы рекомендуем читателям обратиться к фундаменьтальным книгам (Например, В. Феллер ч.1и2. или Гнеденько Курс Т.В.).

В частности, отметим, что линейное преобразование не меняет характера распределения, т.е. из нормальной с.в. получается нормальная случайная величина, а из равномерной - получается равномерная. Рассмотрим пример на равномерное распределение.

Пример 3. Пусть с.в.имеет равномерное распределение в интервале

Найти математическое ожидание с.в.

1) найти плотность

2) не вычисляя функцию найти математическое ожидание с.в..

Решение. 1) Легко заметить, что функция плотностис.в.определяется равенствами (воспользуемся свойством функции плотности)

В интервалефункцияне монотонна: в интервале

функция возрастает, в убывает. На первом участке обратная функцияна второмНа основании формулы (4) имеем

т.е.

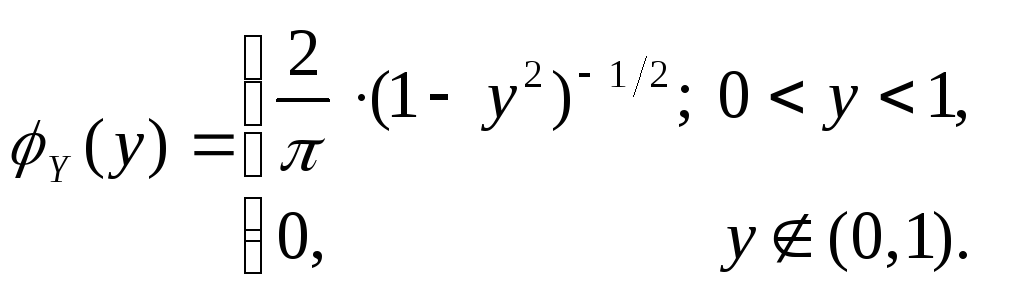
Тогда

.

т.е. .

2) Воспользуемся непосредственно формулой (5)

,

т.е. , оба результата одинаковые.

Задание.1.Вычислить дисперсию и стандарт с.в..

Рассмотрим следующую классическую задачу.

Задача (обратное распределение Коши). Случайная величина имеет распределению Коши с плотностью распределения. Имеем

(см. пункт 7.4. пример 8.)

Вычислить плотность распределения обратной случайной величины

Решение. Функция не определена в нуле, убывает на интервалахимеет однозначную обратную функциюПрименяя формулу () получим

Следовательно, величина, обратная величине, распределённой по закону Коши, также имеет распределение Коши.