Тема 13. Многомерная случайная величина (общие сведения)

1. Многомерная случайная величина

В этом разделе кратко рассмотрим систему случайных величин, гделюбое натуральное число, большее 2. Системаслучайных величин определяется аналогично, что и система двух случайных величин.

Систему случайных величин называютмерной (многомерной)с.в. или случайным вектором.

Многомерная с.в. есть функция элементарного события. Каждому элементарному событиюставится в соответствиедействительных чисел, которые принимают соответственно случайные величиныв результате некоторого испытания (опыта). Векторназываетсяреализациейслучайного вектора

Закон распределения вероятностей мерной случайной величины задается её функцией распределения

(1)

Функция распределения обладает такими же свойствами, как и функция распределения двух случайных величин

В частности, она принимает значения на отрезке :

.

Если , то, то есть монотонно возрастает по каждому аргументу и т.д.

Приводим для системы случайных непрерывных величин основные требования к её функции плотности, функции распределения и определения вероятности попадания случайной-мерной случайных точкив заданной области из-мерного вероятного пространства.

Плотностью распределения системы н.с.в.определяется равенством

(2)

При этом выполняется равенство и длякратного интеграла имеет место равенство

(3) (Контроль).

Вероятность попадания случайной точкив областьимерного пространства выражаетсякратным интегралом

(4)

Функция распределения выражается через плотностькратным интегралом

(5)

Необходимым и достаточнымусловием взаимной независимостислучайных величинявляется равенство

(6)

(7)

Основными числовыми характеристиками мерной с.в.являются:

1. Общее число м.о. равно для всех составляющих, т.е.

2. Общее число дисперсии равно для всех составляющих, т.е.при этом;

3. Общее число ковариаций равно т.е.

при этом

В общем случае ковариации образуют ковариационную (симметрическую) матрицу

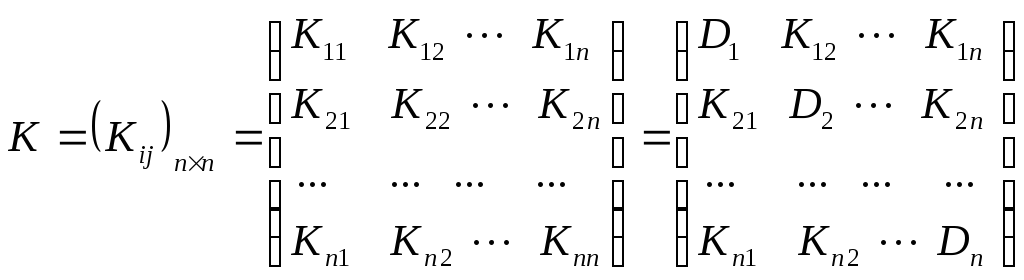
Примечание. На основании теории ковариационных матриц, можно создавать теорию систем линейных уравнений, матричных уравнений, спектральную ковариационную теорию матриц и их теорию квадратичных форм от многих переменных а также закон инерции квадратичных форм и т.д. например, можно построить по схеме книги [Исмоилов Д,….Основы Л.А.и Л.П. 2011; гл.3., параграф 7].

Здесь, мы на этом ограничимся.

2. Характеристическая функция и её свойства

С понятием характеристической функции связаны решение многих задач ряда аналитических разделов математики и её приложения (теоретической физики, механики, вариационное исчисление, теория суммирования арифметических функций и др.), в том числе, и теории вероятностей.

На базе характеристических функций и с помощью теории, развитая в анализе (известная под названием преобразований Фурье), удаётся находить сравнительно простое решение многих задач теории вероятностей. Особенно тех, которые связанны с задачей распределения суммы независимых с.в. и вычисления числовых характеристик случайных величин.

Здесь мы рассмотрим определения, некоторые утверждения (свойства) общего характера, а также как теоретические примеры рассмотрим характеристические функции случайных величин, распределённых по наиболее часто применяемых законов в приложениях.

Определение. Характеристической функцией случайной величины называется комплекснозначная функция, равная математическому ожиданию случайной величины, определённых для всех действительных значений ,т.е. равенством

(8)

где параметр,.

Замечание. Математическое ожидание для комплексной случайной величиныопределяется, как комплексная сумма математических ожиданий реальной и мнимой частей комплексного числа).

Для д.с.в. , принимающая значенияс соответствующими вероятностямихарактеристическая функция определяется формулой

(9)

Следовательно, если с.в. принимает целочисленные значениятои

(10) .

Отсюда получим важный вывод: для дискретной случайной величины имеет место равенстводля любого целого числа.

Для н.с.в. с плотностью характеристическая функция определяется формулой

(11)

Если вспомним дифференциальное равенство , то равенство (10) можно переписать в следующем виде (в форме интеграла Стилтьеса). Для случайной величиныс произвольной функцией распределенияматематическое ожиданиезадаётся с помощью интеграла Стилтьеса, т.е. формулой

(11)

Для непрерывной ограниченной функции и неубывающей ограниченной непрерывной слева функцииинтеграл Стилтьеса(11) существует и его можно определить равенством

.

Так, согласно определению интеграла Стилтьеса, для функции

,

где величина индикатор множества, определяемая равенствами:

Из того, что , то при всех вещественных, следует существование интеграла (11) для всех функций распределения, следовательно, характеристическая функция может быть определена для каждой случайной величины.

Как уже было отмечено, если с.в. принимает целочисленные значения то,, тогда. Этот случай достаточно подробно рассматривался в п. 8.8.

По этой причине, здесь в основном рассмотрим непрерывные случайные величины . При исследовании этого раздела в основном будем следовать учебнику [1].

Теорема 13.1. Характеристическая функция непрерывной случайной величиныравномерно непрерывна на всей прямой и удовлетворяет следующим соотношениям:

1., 2..

Доказательство. В равенстве (10) положим, тогда в силу того, чтоявляется плотностью вероятности распределения н.с.в., получим (свойство -контроля) и, получим. Далее, по определению (11) имеем

.

Остаётся доказать равномерную непрерывность функции . С этой целью рассмотрим разность

,

и оценим её по модулю. Имеем . Пустьпроизвольное число, выберем достаточно большое положительное числотакое, чтобыи подберём столь малое приращениетакое, чтобы для всех. Тогда

последнее неравенство завершает доказательство теоремы.

Теорема 13.2. Если , гдеи- постоянные вещественные числа, то имеет место равенство, гдеиобозначают характеристические функции с.в.и.

Доказательство. По определению (11) имеем цепочку равенств:

.

Что и требовалась доказать.

В качестве приложения этой теоремы найдём характеристическую функцию случайной величины . По теореме 13.2. она равна

.

Задание. На основании формул (12) - (15) найтии. Здесьвероятность наступление события.

Теорема 13.3.Характеристическая функция суммы двух независимых случайных величин равна произведению их характеристических функций.

Доказательство. Пустьинезависимые случайные величины. Тогда очевидно, что вместе синезависимы также случайные величиныи. Отсюда следует, что

.

Это равенство доказывает теорему. Отметим, что эта теорема значительно упрощает сложение независимых случайных величин.

Следствие 1. Еслии каждое слагаемое независимо от суммы предыдущих, то характеристическая функция величиныравна произведению характеристических функций слагаемых, т.е..

Упражнение. Докажите, что еслипостоянные числа и, гдепопарно независимые случайные величины, тогда справедливо равенство

.

Теорема 13.4. Если случайная величина имеет абсолютный моментго порядка, то характеристическая функция величиныдифференцируема,раз и приимеет место

(12) ,

где

Далее по условию теоремы с.в. имеет абсолютный моментго порядка, поэтому он (абсолютный момент) ограничен, т.е.. Следовательно, можно обе части равенства (11) дифференцировать. Тогда получим (12). Из (12) при, получим.

Равенство (12) также называют «формулой вычислении моментов» При помощью этой формулы легко вычислить математическое ожидание и дисперсию н.с.в..

Следствие 2. Математическое ожидание и дисперсия выражается формулами:

(12) .

Задание.Докажите равенство

Замечание. Введём обозначение

(13) ,

(равенство рассматривается для фиксированной ветви логарифмической функции).

Тогда на основании (13) можно проверить следующие равенства

(14) ,;

и с учётом , из равенство (11), находим,.

Следовательно,

Отсюда, получим ещё одну формулу для вычисления математического ожидания и дисперсии случайной величины.

(15) .

Производная го порядка функции логарифма характеристической функции (т.е. функция) в точке, умноженная на число, называетсясемиинвариантом го порядка случайной величины. Первыми двумя семиинвариантами являются математическое ожидание и дисперсия, т.е. момент первого порядка и некоторая рациональная функция моментов первого и второго порядков (см. равенство (14)).

Из теоремы 13.3. непосредственно выводится.

Следствие 3. При сложении суммы двух независимых с.в. их семиинварианты складываются, т.е.

(16) .

Упражнение. Покажите, что справедливы равенства:

1.

2. .