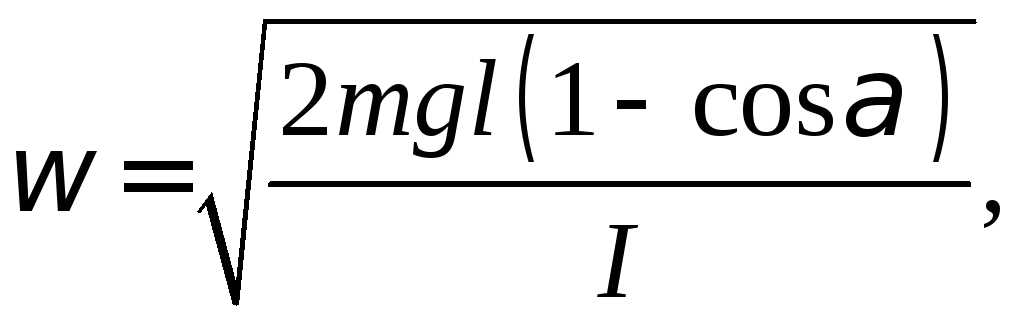- •Министерство образования и науки
- •Введение
- •1.2. Требования к организации лабораторной работы
- •1.3. Порядок проведения лабораторных работ
- •1.4. Требования к оформлению отчета по лабораторной работе
- •1.5. Права, ответственность и обязанности преподавателя
- •1.6. Права, ответственность и обязанности студента
- •1.7. Методика и организация занятий физического практикума
- •1.8. Порядок проведения занятий физического практикума в течение семестра
- •1.9. Технология контроля и оценки знаний, умений и навыков обучающихся по балльно-рейтинговой системе и сроки их проведения
- •Структура и содержание знаний, умений и навыков студентов по лабораторным занятиям дисциплины физика и вопросов, позволяющих их оценить по балльно - рейтинговой системе
- •Многобальная система оценки знаний
- •Лабораторная работа № 1.1 оценка случайной погрешности и доверительной вероятности прямых и косвенных измерений
- •Задание 1. Определение плотности твердого тела Введение
- •Задание 1.1. Определение плотности твердого тела правильной геометрической формы
- •Порядок выполнения работы
- •Задание 1.2. Определение плотности твердого тела гидростатическим взвешиванием
- •Задание 1.3. Определение плотности твердых тел с помощью пикнометра
- •Контрольные вопросы для допуска к работе
- •Задание 2. Оценка случайной погрешности и доверительной вероятности прямых и косвенных измерений
- •Задание 2.1. Исследование зависимости погрешности измерений от квалификации персонала и способа измерения
- •Задание 2. 1.2. Исследование зависимости погрешности измерений от способа измерения
- •Задание 2. 3. Расчет доверительного интервала и доверительной вероятности методом Стьюдента
- •Контрольные вопросы для допуска к работе
- •Задание на срс. Проработать следующие вопросы и задания к сдаче отчета
- •Лабораторная работа № 1.2 определение ускорения силы тяжести
- •Теоретическая часть
- •Порядок выполнения работы
- •Лабораторная работа № 1.3.
- •Задание 1. Определение ускорение силы тяжести с помощью математического маятника
- •Порядок выполнения работы
- •Задание 3. Определение положения центра тяжести физического маятника методом обращения
- •Задание 4. Определение ускорения силы тяжести оборотным маятником
- •Лабораторная работа № 1.4 изучение законов динамики поступательного движения на машине атвуда
- •Теоретическая часть
- •1.Метод измерения и расчетные соотношения
- •2. Описание экспериментальной установки
- •Спецификация измерительных приборов
- •3. Обработка результатов измерений
- •Задание срс. Проработать следующие вопросы
- •Лабораторная работа 1.5
- •Определение коэффициента
- •Трения скольжения при движении твердого тела
- •По наклонной плоскости
- •Описание экспериментальной установки
- •Порядок выполнения работы
- •Спецификация измерительных приборов
- •Задание 1. Определение значения коэффициента трения скольжения по углу
- •Массы брусков, углыи коэффициенты трения
- •Задание 2.Определение значения коэффициента трения из опытов по скольжению бруска по наклонной плоскости
- •Результаты измерений при 10°
- •Результаты измерений при
- •Лабораторная работа № 1.6 определение модуля сдвига и кручения
- •Теоретическая часть
- •1.Механика упругих тел
- •Лабораторная работа № 1.6 а определение модуля сдвига методом крутильных колебаний
- •Теория метода
- •Экспериментальная часть Описание установки
- •Порядок проведения эксперимента и обработка результатов
- •Задание на срс. Проработать следующие вопросы и задания к сдаче отчета
- •Лабораторная работа № 1.6 б определение модуля юнга по изгибу балки
- •Теория метода
- •Измерение модуля Юнга из изгиба
- •Экспериментальная часть Описание установки
- •Порядок проведения эксперимента и обработка результатов
- •Задание на срс. Проработать следующие вопросы и задания к сдаче отчета
- •Лабораторная работа № 1.7 определение силы сопротивления грунта при забивке сваи на модели копра
- •Теоретическая часть
- •Экспериментальная часть Описание экспериментальной установки
- •Порядок выполнения работы
- •Спецификация измерительных приборов
- •Измерение перемещения сваи после соударения
- •Обработка результатов измерений
- •Лабораторная работа № 1.8 изучение законов динамики вращательного движения
- •Лабораторная работа № 1.8а изучение законов динамики вращательного движения на маятнике обербека
- •Теория метода
- •Экспериментальная часть Порядок выполнения работы
- •Спецификация измерительных приборов
- •Измерение времени движения груза
- •Обработка результатов измерений
- •Задание на срс. Проработать следующие вопросы и задания к сдаче отчета
- •Лабораторная работа № 1.8 б
- •Экспериментальная часть Описание экспериментальной установки
- •Порядок выполнения работы
- •Спецификация измерительных приборов
- •Задание 1. Определение момента инерции маховика
- •Задание 2. Определить значение момента инерции маховика, используя непосредственно уравнение (4)
- •Обработка результатов измерений
- •Угловое ускорение маховика и момент сил натяжения нити для опытов с различными массами грузов
- •Задание на срс. Проработать следующие вопросы и задания к сдаче отчета
- •Лабораторная работа № 1.8 в определение момента инерции тела с помощью крутильного маятника и проверка теоремы штейнера
- •Теоретическая часть
- •Экспериментальная часть Порядок выполнения работы
- •Задание на срс. Проработать следующие вопросы
- •Классификация ударов
- •Лабораторная работа № 1.9а изучение закона сохранения импульса
- •Теория метода
- •Задание 1. Сравнение импульсов и энергий до и после взаимодействия
- •Задание 2. Простейшая оценка погрешности измерений
- •Контрольные вопросы для допуска к работе
- •Задание на срс. Проработать следующие вопросы и задания к сдаче отчета
- •Лабораторная работа № 1.9 б проверка закона сохранения момента импульса
- •Теория метода
- •Задание 1. Определение моментов импульсов и кинетической энергии маятников
- •Задание 2. Оценка погрешности измерений
- •Задание на срс. Проработать следующие вопросы и задания к сдаче отчета
- •Калибровка
- •Литература
Задание на срс. Проработать следующие вопросы и задания к сдаче отчета
1.Понятие механической системы. Что такое замкнутая система? Что такое консервативная система?
2.Что называется импульсом тела? Что называется импульсом механической системы?
3.Что называется кинетической, потенциальной, полной механической энергией системы?
4.Что называется моментом импульса системы?
5.Дайте устные и аналитические формулировки законов сохранения импульса, механической энергии и момента импульса.
6.Роль законов сохранения в физике.
7.Когда для описания физических систем использование законов сохранения оказывается предпочтительнее по сравнению с использованием законов динамики?
8.Приведите примеры процессов в реальных системах, когда эти системы можно считать замкнутыми. Выбор обоснуйте.
9. Почему силы возникающие при ударе, велики?
10. Почему к явлению удара можно применить закон сохранения количества движения?
11. Почему в данной работе можно применить закон сохранения энергии?
12. К какому моменту времени относятся уравнения
![]() (1)
(1)
![]() (2)
(2)
13. Объясните, почему скорость шара после соударения равна нулю?
14. Каков будет характер движения шаров после удара, если оба электромагнита выключить?
15. Сформулируйте закон сохранения момента количества движения.
16. Запишите закон сохранения момента количества движения для случая абсолютно упругого удара нули.
17. Можно ли считать, что кинетическая энергия пули в случае неупругого удара плотностью переходит в потенциальную энергию маятника?
18. Выведите формулу погрешности. Какими членами в формуле погрешности можно пренебречь?
19 Как практически определить момент инерции системы?
Лабораторная работа № 1.9 б проверка закона сохранения момента импульса
Цель работы: проверить закон сохранения момента импульса и энергии при неупругом взаимодействии маятников, оценить погрешность измерений.
Приборы и принадлежности: специальная установка, секундомер, линейка.
Теория метода
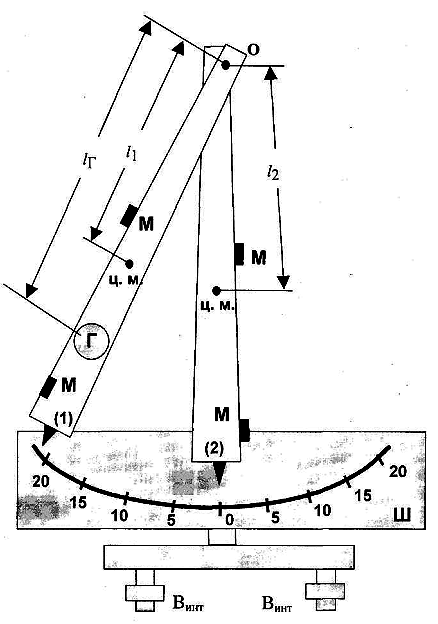
Описание установки. Установка состоит из двух физических маятников (1) (масса т1) и (2) (масса т2), которые независимо могут вращаться вокруг общей оси О (рис. 1). Маятники снабжены магнитами М, с помощью которых они стягиваются и могут вращаться вокруг оси О, как единое целое. Для изменения момента инерции к маятнику 1 может быть прикреплен добавочный груз Г (масса тг).
|
|
| |
|
а) |
б) | |
|
|
Рис.1 Установка для изучения неупругого соударения физических маятников
| |
На каждом маятнике красной меткой указано положение центра масс (ц.м.), расстояние которого от оси вращения равны, соответственно, l1 и l2.
Очевидно, центр масс маятника с добавочным грузом находится от оси вращения на расстоянии
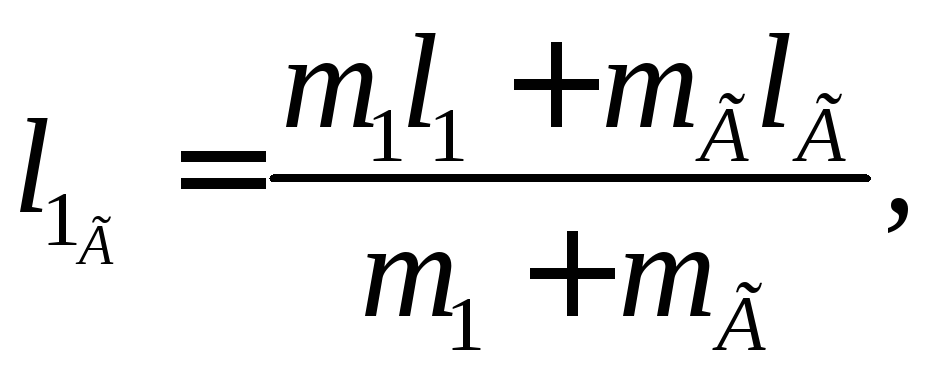
где lг - расстояние центра груза от оси вращения.
Центр масс двух маятников с добавочным грузом находится от оси вращения на расстоянии
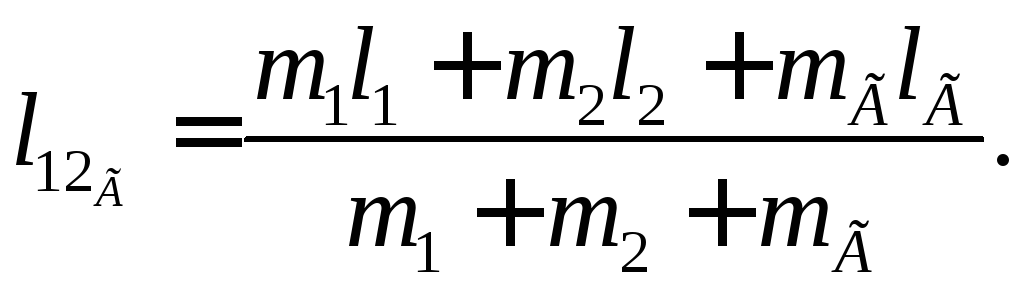
Если добавочный груз отсутствует, то это расстояние
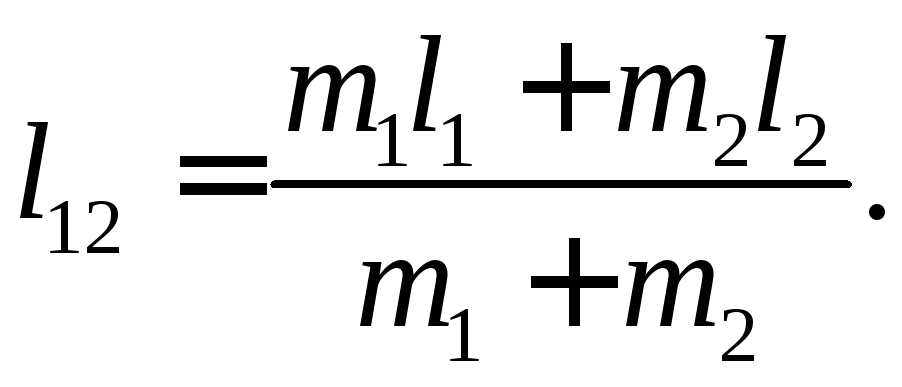
Угол отклонения маятника от положения равновесия определяется по шкале Ш. В положении равновесия маятники располагаются так, чтобы их визиры находились против нулевой отметки шкалы Ш. Это достигается с помощью винтов В в основании установки.
Если отклонить один из маятников, и закрепить в отклоненном положении, а второй отклонить и отпустить, то он будет совершать колебательное движение около положения равновесия.
Если же один из маятников отклонить из положения равновесия на угол α (второй при этом оставить в положении равновесия) и отпустить, то после столкновения маятников они начнут двигаться как одно целое и отклонятся от положения равновесия на угол β.
Два физических маятника, имеющие общую горизонтальную ось вращения образуют замкнутую систему в момент прохождения ими положения равновесия (в этом положении моменты сил тяжести равны нулю, а других моментов относительно оси вращения просто нет). Следовательно, при прохождении положения равновесия для этой системы выполняется закон сохранения момента
![]()
где I1 и I2- моменты инерции маятников относительно оси вращения;
![]() и
и
![]() - их
угловые скорости в положении равновесия
до их соударения;
- их
угловые скорости в положении равновесия
до их соударения;
![]() и
и
![]() - их
угловые скорости после взаимодействия.
- их
угловые скорости после взаимодействия.
До
взаимодействия второй маятник покоится
(![]() ),
а
после взаимодействия
оба маятника движутся как единое целое
(
),
а
после взаимодействия
оба маятника движутся как единое целое
(![]() )
и
поэтому закон сохранения
момента импульса в проекции на ось
вращения принимает вид:
)
и
поэтому закон сохранения
момента импульса в проекции на ось
вращения принимает вид:
![]() (1)
(1)
Моменты инерции маятников можно найти, зная их периоды колебаний
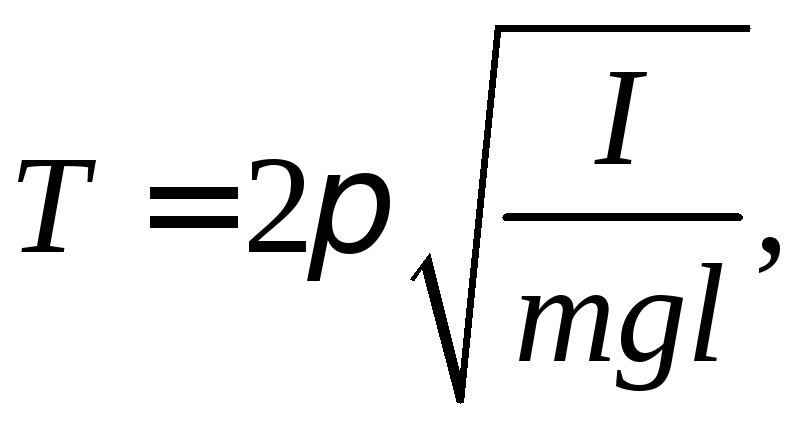
где l - расстояние от оси вращения до центра масс маятника.
Таким образом, момент инерции маятника 1
(2)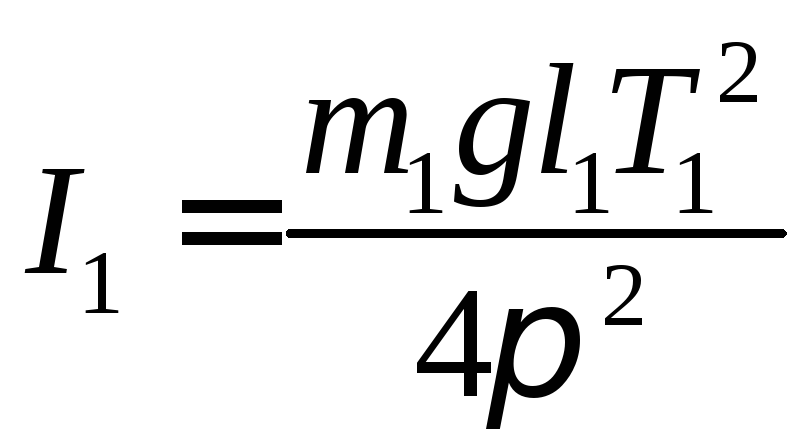
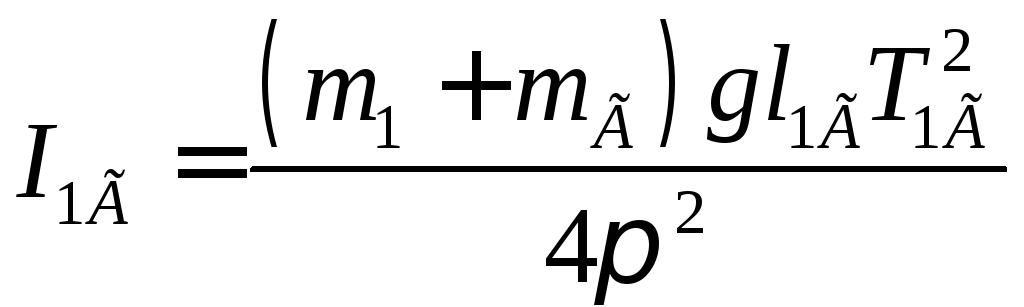 (с
грузом),
(с
грузом),
момент инерции системы из двух маятников
(3)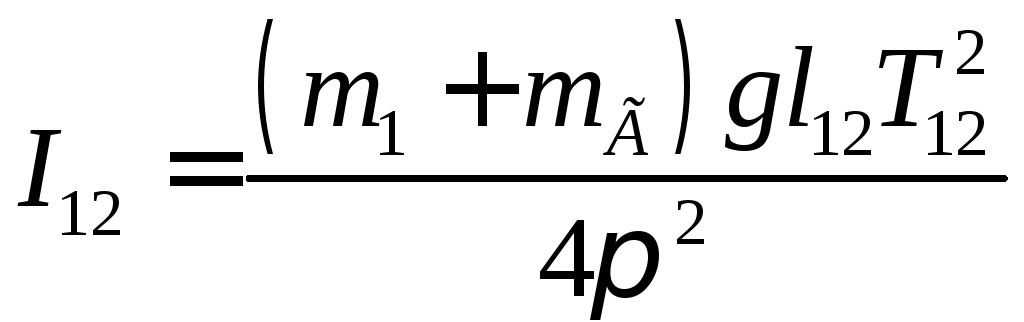
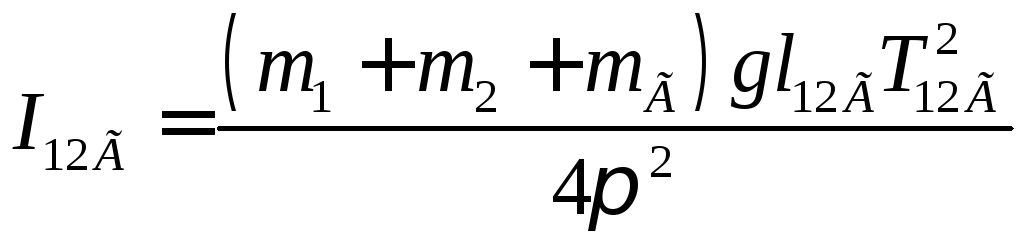 (с
грузом),
(с
грузом),
где l12 и l12Г расстояние от оси до центра масс системы из двух маятников без дополнительного груза и с грузом;
T12 и T12Г - период колебания системы из двух маятников
(без груза и с грузом).
При отклонении маятника от положения равновесия на угол α центр масс
|
|
его
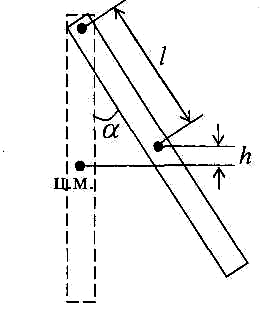
поднимется на высоту (рис. 2)
можно найти угловую скорость маятника в момент прохождения положения равновесия:
|
|
Рис.2
|
где
![]() -
энергия колеблющегося маятника при
прохождении положения равновесия,
-
энергия колеблющегося маятника при
прохождении положения равновесия,
mgh - энергия маятник, отклоненного на угол α (при этом его центр масс поднят на высоту h).
В наших опытах первоначально маятник 1 отклоняется от положения равновесия на угол α и, следовательно, его угловая скорость при прохождении положения равновесия (т.е. перед взаимодействием (столкновением) с маятником В))-
(4)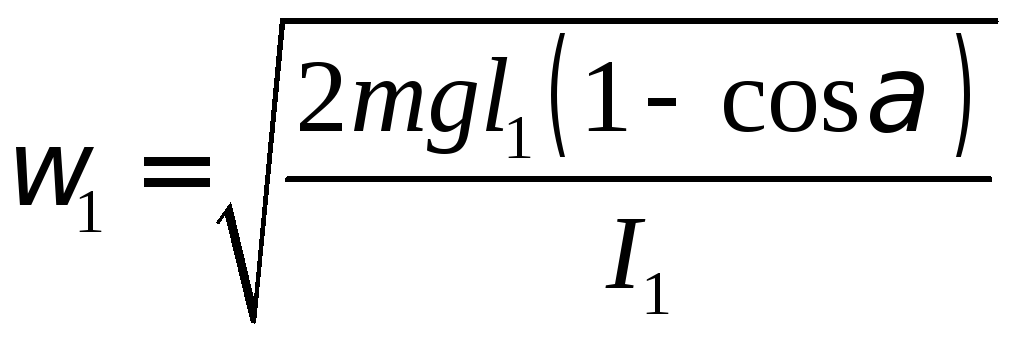
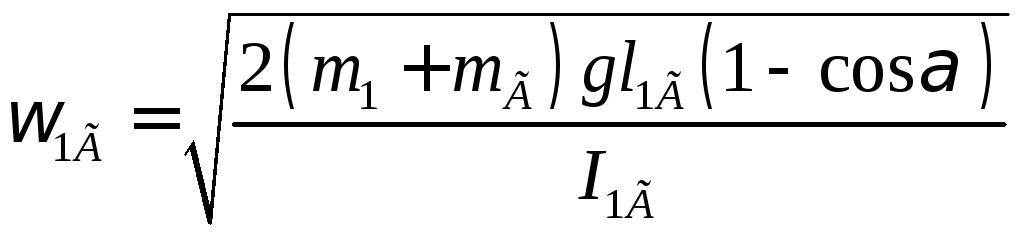 (с
грузом)
(с
грузом)
После столкновения система из двух маятников отклоняется на угол β, и следовательно, их начальная угловая скорость в положении равновесия
(5)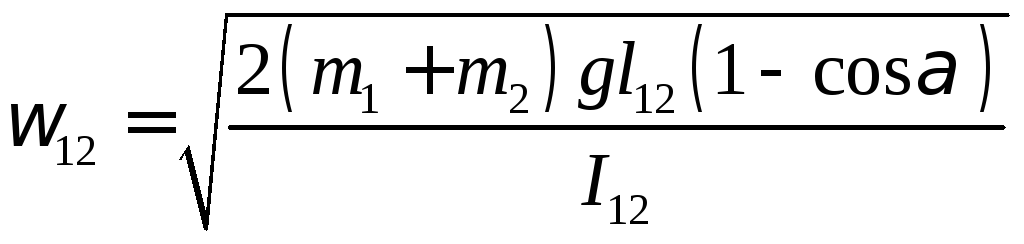
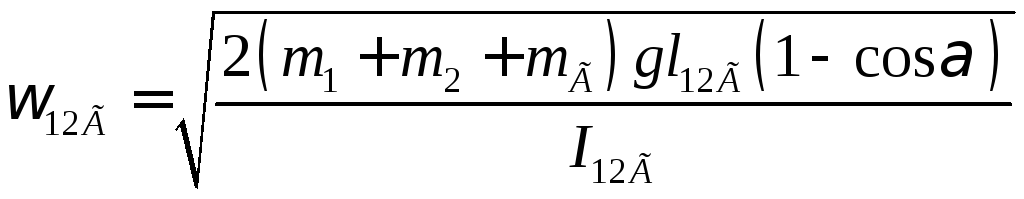 (с
грузом)
(с
грузом)