2.2.5. Двоичный счетчик с произвольным порядком счета
Состояние счетчика с произвольным порядком счета с приходом очередного входного сигнала изменяется на величину, отличную от единицы. Исходными данными является порядок перехода счетчика в последующее состояние.
В качестве примера рассмотрим восьмиразрядный счетчик и изменением сначала четных состояний счетчика, а затем нечетных. Таблица функционирований такого счетчика представлена ниже (табл. 5).
Таблица 5
|
Состояние счётчика |
Функция перехода | ||||||||
|
№ |
Предыдущее |
Последующее |
|
|
| ||||
|
|
|
|
|
|
| ||||
|
0 |
0 |
0 |
0 |
0 |
1 |
0 |
0 |
▲ |
0 |
|
1 |
0 |
1 |
0 |
1 |
0 |
0 |
▲ |
▼ |
0 |
|
2 |
1 |
0 |
0 |
1 |
1 |
0 |
1 |
▲ |
0 |
|
3 |
1 |
1 |
0 |
0 |
0 |
1 |
▼ |
▼ |
▲ |
|
4 |
0 |
0 |
1 |
0 |
1 |
1 |
0 |
▲ |
1 |
|
5 |
0 |
1 |
1 |
1 |
0 |
1 |
▲ |
▼ |
1 |
|
6 |
1 |
0 |
1 |
1 |
1 |
1 |
1 |
▲ |
1 |
|
7 |
1 |
1 |
1 |
0 |
0 |
0 |
▼ |
▼ |
▼ |
В соответствии с таблицей функционирования
счетчика определим функции перехода
каждого триггера
(см. табл. 5). На основании таблицы переходов
триггеров составим карты функций
переходов для каждого триггера:
(рис. 14).
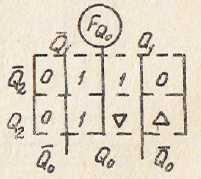
Рис. 14
Заменяя функции переходов в картах, изображенных на рис. 14, значениями функций управления J и K из словаря переходов (см. табл. 2), получаем карты Карно для J и K входов каждого триггера счётчика (рис.15).
Рис. 15
Минимизируя, получим логические уравнения входов J и K:
;
;
.
Из этих выражений следует, что на J и K входы второго триггера следует подать прямой выход с первого триггера, на J и K входы нулевого триггера - конъюнкцию логических переменных с прямых выходов второго и первого триггеров. На входы первого триггера необходимо подать потенциал соответствующий логической единице.
Схема счетчика, построенного в соответствии с полученными результатами, приведена на рис. 16.
Рис. 16
2.2.6. Недвоичный счетчик
Недвоичные счетчики имеют
.
Принцип их построения состоит в исключении
некоторых устойчивых состояний обычного
двоичного счетчика. Исключающие состояния
счетчика называют избыточными. Исключение
из избыточных состояний осуществляется
с помощью введения обратных связей
внутри счетчика. Алгоритм синтеза
недвоичного счетчика аналогичен
вышеизложенному. В качестве примера
рассмотрим работу счетчика с
=5
, принимающего последовательно состояния
0, 1, 3, 5, 7.
Счетчик строится на 3 триггерах, так как
m=[
]=3.
Число избыточных состояний
.
Таблица функционирования счетчика и
функций перехода имеет вид табл. 6.
Таблица 6
|
Состояние счётчика |
Функция перехода | ||||||||
|
№ |
Предыдущее |
Последующее |
|
|
| ||||
|
|
|
|
|
|
| ||||
|
0 |
0 |
0 |
0 |
0 |
0 |
1 |
0 |
0 |
▲ |
|
1 |
0 |
0 |
1 |
0 |
1 |
1 |
0 |
▲ |
1 |
|
3 |
0 |
1 |
1 |
1 |
0 |
1 |
▲ |
▼ |
1 |
|
5 |
1 |
0 |
1 |
1 |
1 |
1 |
1 |
▲ |
1 |
|
7 |
1 |
1 |
1 |
0 |
0 |
0 |
▼ |
▼ |
▼ |
Карты функций переходов для каждого
триггера
показаны
на рис. 17.
Рис. 17
Избыточные, исключенные состояния счетчика в клетках карт отмечены знаком "-". На основании представленных карт построим карты Карно функций управления J и K входами триггеров (рис. 18).
Рис. 18
Учитывая, что в клетках с исключенными состояниями, функция не определена, при проведении контуров в картах: Карно необходимо их включать с целью упрощения функций. После минимизации получим:
;
;
;
Схема счетчика с учетом полученных выражений представлена на рис. 19.
Рис.
19