25.Расчет жб элементов на местное сжатие(смятие)

В случае приложения нагрузки на ограниченную площадь имеет место сжатие, при этом прилегающие слои бетона припятствуют развитию пластической и поперечной деформации,в результате прочность повышается. R_b,loc ≥ R_b Примеры приложения местных нагрузок:- опирание балок на стены, стыки колонн, опирание балок на стыки колонн.Расчет на местное сжатие безкосвенного армирования,

– зависит от вида нагрузки (сосредоточенная или равномерно распределенная по площади), – расчетное сопротивление бетона смятию,

– максимальная расчетная площадь, вызванная вовлечением в работу смежных слоев бетона.

Для определения необходимо выполнять следующие правила:

1.Центры тяжести сечения и должны совпадать.

2.Граница расчетной площади откладывают от каждой стороны площади на расстояние, равное соответствующему размеру этих сторон.

Примеры определения и А) Площадь местного сжатия располагается вдали от краев элемента

Б)Площадь местного сжатия располагается по всей ширине элемента

,

В)Площадь местного сжатия располагается у края элемента

Г)Площадь местного сжатия расположена в углу элемента

Д)Площадь местного сжатия расположена у одного края

,

Е) Площадь местного сжатия располагается в глубине элемента

Расчет элементов на сжатие с косвенным армированием выполняется по формуле: , – приведенное, с учетом косвенной арматуры, расчетное сопротивление бетона смятию.

,

-площадь заключенная внутри контура сеток косвенного армирования.

,,

- приведенная площадь к условной полосе, вырезанной из элемента. ,

S – шаг сеток

26. Расчет железобетонных элементов на продавливание. Выполняется при расчете фунд. плиты, плитной части стаканного фунд-та и безбалочного перекрытия. При расчете на продавливание рассматривают расчетное сечение расположенное вокруг зоны передачи нагрузки на элемент на расстояние h_o/2 нормально к его продольной оси, по поверхности которой действуют касательные усилия от сосредоточенных сил и изгибающих моментов. Данные касательные усилия по площади расчетного сечения восприняты бетоном работающим на растяжение и расположены по обе стороны от расчетного сечения на расстоянии h_o/2 поперечной арматуры с расчетным сопротивлением R_sw. Расчет ж/б элемента на продавливание при действии только сосредоточенной силы. В случае отсутствия поперечной арматуры расчет производится по след. формуле: F≤Fв,ult где: F- сосредоточенная продавливающая сила; Fв,ult- предельное значение, которое м.б. воспринято бетоном. Fв,ult =Rвt*Ав; Ав- площадь расчетного поперечного сечения. Ав=U*h_o; U- периметр контура расчетной площади. U=(а+ h_o/2*2+в+ h_o/2)*2=2*(2*h_o+а+в); h_o-усредненное рабочая высота сечения. h_o= h_oх+ h_oу/2

Несущая способность проверяется по условию: F≤Fв,ult+ F_sw,ult ; F_sw,ult- предельное усилие, воспринимаемое в поперечной арматуре при продавливании. F_sw,ult=0,8*q_sw*U; q_sw-усилие поперечной арматуры на единицу длины контура расчетного сечения. q_sw= R_sw*А_sw/ S_w; А_sw-площадь сечения поперечной арматуры, расположенной с шагом S_w по обе стороны от контура расчетное сечение. Расчет элементов на прдавливание при действии продавливающей силы F и изгибающего момента N. 1) Элемента без поперечной арматуры. F/ Fв,ult+М/ Мв,ult≤1; Мв,ult-предельный изгибающий момент который воспринят бетоном в расчетном поперечном сечении. Мв,ult= Rвt*Wв*h_o; Wв-момент сопротивления расчетного сечения. Wв=В*А/6; А=а+ h_o; В=в+ h_o 2) При действии момента в двух взаимно перпендикулярных направлениях и при отсутствии поперечной арматуры. F/ Fв,ult+М_х/Мвх,ult +М_у/Мву,ult ≤1; Мвх,ult= Rвt*Wвх*h_o ; Wвх=В*А²/6; Мву,ult= Rвt*Wву*h_o; Wву=В²*А/6; 3) При действии момента в первой плоскости на элемент с поперечной арматурой. F/ Fв,ult+ F_sw,ult+ М/Мв,ult +М_sw,ult ≤1; М_sw,ult-предельный момент которы воспринят поперечной арматурой. М_sw,ult=0,8*q_sw*W_sw; W_sw-момент сопротивления наружной границы, вовлекающей в работу поперечную арматуру. W_sw= В*А²/6; А=а+2h_o; В=в+2h_o 4) При действии момента в двух главных плоскостях на элемент с поперечной арматурой. F/ Fв,ult+ F_sw,ult+ Мх/Мвх,ult+М_swx,ult+ Му/Мву,ult+М_swy,ult≤1 При расположении поперечной арматуры вдоль главных осей (крестообразно) расчетные контуры сечения будут определятся по следующим правилам

27. Понятие о предварительном напряжении ж/б конструкций. Назначение величины предварительного напряжения. Способы создания предварительного напряжения ж/б конструкций. Понятие о предварительном напряжении ж/б конструкций. Идея предварительных напряжений заключается в том, что в рабочей арматуре создаются предварительные напряжения растяжению и арматура в момент отпуска стремится сократиться обжимая бетон. Суть предварительного напряжения заключается в трещиноустойчивости с деформативности конструктивных элементов. Приложенная нагрузка предварительно напряженной конструкции должна сначала выбрать сжимающие напряжения от предварительно напряженного бетона и после этого начнут появляться растягивающие напряжения, при этом трещины будут образовываться при более высокой нагрузке, по сравнению с конструкцией без преднапряжения. При более высоких нагрузках ширина раскрытия трещин достигнет предельных значениях. При этом в рабочей растянутой арматуре будут возникать высокие растягивающие напряжения. Поэтому в данных конструкциях в качестве рабочей арматуры используют высокопрочную арматуру(все виды канатов, проволочная арматура. Вр 1200-1500, стержневая арматура, А600) Назначение величины предварительного напряжения. Чем выше предварительные напряжения тем эффективней оно сказывается на работе ж/б элемента. Однако при назначении и величины предварительных напряжений необходимо учитывать следующие факторы: 1) Возможность обрыва напрягаемой арматуры. 2) Возможность развития пластических деформаций. 3) Стараться не занизить данную величину т.к. будет утерян эффект преднапряжения. По нормам предварительных напряжений в рабочей арматуре назначаются исходя из следующих условий: Q_sp+p≤R_s.ser ;Q_sp-p≤0,3R_s.ser р-допустимое отклонение предварительных напряжений. Начальное напряжение в бетоне должны отвечать следующим требованиям: - при уменьшении напряжения в результате приложенной нагрузки : Q_вр=(0,85…0.95)*R_вр при увеличении напряжения после приложенной нагрузки: Q_вр=(0,6…0,7)*R_вр При создании предварительного напряжения возможны неточности вызванные различными производственными факторами учитываемые коэффициентом точности напряжения. γ_sp=1±∆ γ_sp; ∆sp=0,1 (знак + применяется если увеличиваем значение Q_sр сверх проектного, учитывается при расчете по прочности в стадии обжатия; знак – применяется, если снижается Q_sр что плохо влияет на работу конструкции (при расчете на закрытие трещин) Напряжение в бетоне зависит от напряжения в арматуре, которая с учетом неточности создавая преднапряжения определяется по формуле: Q_sр= Q_sр* γ_sp Способы создания предварительного напряжения ж/б конструкций. 1. Механический- рабочая предварительно напряженная арматура натягивается при помощи гидравлических домкратов, данный способ является самым технологичным. При данном способе трудно определить величину передаваемого от домкратов величину предварительных напряжений арматуры. 2. Электрический- натягиваемую арматуру разогревают до 300-350 градусов, затем укладывают в форму разместив в нужных местах ограничители деформаций. При наборе прочности бетона арматура остывает стремясь сократиться. 3. Электротермомеханический – сочетает механическое напряжение (20-30% от общего усилия напряжения) с электротермическим. 4. Физико-химический- суть в самонапряжении ж/б конструкции благодаря использования бетона на расширяющемся цементе. Такой бет после достижения прочности 15-20мПа. Обеспечивающий надежное сцепление с арматурой расширяется вынуждая удлиняться арматуру. Применяется при устройстве напорных труб, в которых рабочая арматура кольцевая. Кроме того существует 2 метода натяжения арматуры : 1. На упоры- арматура натягивается на упоры механическим способом и закрепляется на них, затем конструкция бетонируется, а после достижения бетона прочностной прочности =0,8 R_в арматура срезается с упоров и обжимает бетон. 2. На бетон- при создании предварительного напряжения в больших пролетных конструкциях. Изготавливается бетонный элемент иногда малоармированый в котором предусмотрены пазы или канылы для размещения предварительно напряженной арматуры. Пазы и каналы выполняют из гафрированной трубы, диаметр которой на 5-15мм больше диаметра напрягаемой арматуры. Каналы могут выполняться из свежее уложенной бетонной смеси. В пазы и каналы заводят напрягаемую арматуру и при достижении бетонной передаточной прочности осуществляют ее напряжение закрепляя на торцах элемента. После натяжения арматуры в пазы и каналы иньецируется раствор, а с наружной стороны закрывают защитным слоем в виде торкрет бетона

28. Напряжение в бетоне при обжатии. При расчете предварительно напряженных конструкций возникает необходимость напряженного состояния в бетоне на различных этапах его работы от усилия предварительного обжатия. Например: необходимо определить максимальное усилие обжатие бетона с целью предотвращения разрушения ж/б элемента. Напряжение в бетоне определяется в предположении его упругой работы. В расчетах предварительного напряжения элементов используются приведенные геометрические характеристики площадь сечения арматуры заменяется эквивалентной площадью бетона, исходя из условия равенства относительной деформации бетона и арматуры.

Приведенная Sсеч. к бетону: A_red= А_в+α*А_s+α_р+ А_sр+ α_р* А_sр´+ α*А_s´ ; α=E_s/Е_в; α_р= E_sр/Е_в; А_в=в*h Статический момент приведенного сечения к бетону относительно нижней грани сечения. S_red=А_в*h/2+α* А_s*а+ α_р* А_sр*а_р+ α_р* А_sр´*(h-а´_р )+α* А_s´*(h-a´) Расстояние от нижней грани сечения до центра тяжести приведенного сечения. У_о= S_red/ A_red Момент инерции приведенного сеч к бетону относительно приведенного центра тяжести сечения У_red= У_в+ А_в(h/2-у_о)²+ α*А_s*у_s²+ α_р* А_sр*у_sp²+ α_р* А_sр´*у_sp´²+ α*А_s´*у´_s² Составим уравнение равновесия всех сил на продольную ось элемента: Q_вр= Q_sр*A_sp Составим данное уравнение статики, получим усилия предварительного обжатия бетона: Р= Q_вр* A_sp- Q_s*A_s +Q_sр´*A_sp´-Q_s´*A_s´ Для определения экц. l_op составляется уравнение равновесия изгибающих моментов относительно приведенного центра тяжести сечения: Р* l_op- Q_s´*A_s´*у_s´+ Q_sр´*A_sp´*у_sp´-Q_sр*A_sp *у_sp+ Q_s*A_s *у_s=0 Напряжение в бетоне при обжатии находятся как внецентренно сжатого бетонного элемента исходя из упрощенной (упругой) его работы. Q_вр=Р/ A_red±Р* l_op*у_о/ У_red±М* у_о/ У_red Напряжения обжатия могут определяться на различных стадиях работы, например на уровне центра тяжести напрягаемой растянутой арматуры. Q_вр=Р/ A_red+Р* l_op*у_о/ У_red-М* у_sp/ У_red

30. Потери предварительного напряжения.Со временем предварительные напряжения уменьшаются из-за специфических свойств ж/б. Различают 2 вида потерь: 1) потери δ_loss1 (возникают при изготовлении конструкции и при обжатии бетона) 2) потери δ_loss2 (возникают после обжатия бетона) Первые потери: 1) ∆δ₁ от релаксации напряжений в арматуре. 2) ∆δ₂ от температурного перепада, определенного как разность температур в натянутой арматуре- в зоне нагрева и устройства воспринимающего напряжение при нагреве конструкции. 3) ∆δ₃ от деформации стальной формы при неодновременном напряжении арматуры на форму. 4) ∆δ₄ от деформации анкеров натяжных устройств. Вторые потери: 1) ∆δ₅ –от усадки бетона в процессе набора им прочности. 2) ∆δ₆ –от ползучести бетона, которая сдерживаемая зависанием на арматуре влечет к релаксации напряжений. 1) При напряжении арматуры на упоры потери будут определяться: δ_loss= δ_loss1+ δ_loss2 ; δ_loss1=∆δ₁+∆δ₂+∆δ₃+∆δ₄ ; δ_loss2=∆δ₅+∆δ₆ 2) При натяжении арматуры на бетон: δ_loss1=∆δ₄ ; δ_loss2=∆δ₅+∆δ₆ Суммарные потери могут составлять 200-300Мпа но не менее 100Мпа

Для ж/б конструкций значение предварительного напряжения арматуры

σsp принимают:не более 0,9Rs,n - для горячекатаной и термомеханическиупрочненной арматуры; не более 0,8Rs,n - для холоднодеформированной арматуры и арматуры канатов. При расчетах конструкций учитывают снижение созданного предварительного напряжения, вследствие потерь, происходящих до передачи усилий натяжения на бетон (первые потери) и после натяжения на бетон (вторые потери).Первые потери включают в себя потери от релаксации напряжений в арматуре, потери от температурного перепада, потери от деформации анкеров и форм (упоров).Вторые потери включают в себя потери от усадки и ползучести бетона.Передаточная прочность бетона Rвр - прочность бетона к моменту начала его обжатия, контролируемая аналогично классу бетона по прочности на сжатие.Пердаточную прочность бетона следует принимать не менее 15 МПа и не менее 50% принятого класса бетона по прочности на сжатие.

При расчете предварительно напряженных элементов по прочности следует также учитывать возможные отклонения предварительного напряжения вследствие погрешностей, вызванными производственными факторами. Коэффициент точности натяжения γsp принимают равным 0,9 при благоприятном влиянии предварительного напряжения и 1,1 при неблагоприятном влиянии.

29. Последовательность изменения напряженного состояния в предварительно напряженных элементах.Предварительное напряжение создается путем натяжения арматуры на упоры.1.Состояние ж/б элемента до загружения.

2. Конструкция замоноличивается (укладывается бетон), бетон затвердевает и в арматуре имеет место основная часть первых потерь предварительного напряжения δ_loss1=δ _l1

3. После приобретения бетоном передаточной прочности R_вр арматуру освобождают с упоров и напряжения в арматуре снижаются за счет упругого обжатия бетона. E_s=E_в

4. Со временем наблюдается уменьшение напряжения в арматуре за счет накапливания двух потерь предварительного напряжения.

Состояние после загружения. 5. После приложения нагрузки напряжения от нее суммируются с напряжениями предварительного обжатия и при некотором значении нагрузки напряжения обжатия на уровне центра тяжести растянутой предварительного напряжения арматуры =0.

6. С увеличением нагрузки начинают появляться пластические деформации (стадия образования трещин) т.е. напряжения в бетоне растянутой зоне достигает предельных значений т.е. R_вt,ser ; E_s=E_в ; δ_sp/ E_s= R_вt.ser/ E_вt.pl= R_вt.ser/λ* E_в=R_вt.ser/0,5* E_в= δ_sp=R_вt.ser*2*E_s=E_в=2*α*R_вt.ser

7. Наблюдается появление в нижней растянутой зоне бетона трещин. Напряжение в бетоне сжатой зоны не достигнет предельных значений. Данная стадия характерна для нехрупкого разрушения. 8. Напряжения достигли предельных значений.

При достижении предварительных значений напряжений в бетоне и арматуре наступает разрушение элемента, что соответствует 3 ст. состояния ж/б элементов.

31. Общие положения расчета по образованию трещин в железобетонных элементах. Расчет по образованию нормальных трещин в железобетонных элементах. Цель расчета заключается в определении продольной силы N_crc или изгибающего момента М_crc которые вызывают в растянутой зоне бетонного напряжения = R_вt.ser т.е. силы или моменты, при котором начинается трещинообразование в растянутой зоне элемента. Предполагается, что трещина в расчетных сечениях не образовывается, если усилие М и N от внешних нагрузок не превышают N_crc и М_crc т.е. N≤ N_crc ; М≤ М_crc . Если трещины не образовываются, то расчет на раскрытие трещин не производится. Расчет по образованию нормальных трещин в железобетонных элементах. Напряжения в бетоне и растянутой арматуре принимаются по данным первой ст. напряжения состояния. Напряжения в бетоне растянутой зоны распределены равномерно с ординатой R_вt.ser

Поскольку, в элементах без преднапряжения трещины образуется при нагрузке 0,1…0,15 от разрушающей, а в элементах с преднапряжением 0,7…0,8 от разрушающей, то напряжение в бетоне для элементов без преднапряжения определяется с учетом упругих деформаций. Напряжение в напрягаемой арматуре: (δ_sр2- δ_loss)*γ_sp+ Q_s=( δ_sр2- δ_loss)* γ_sp+2*α* R_вt.ser , Необходимость расчета по образованию трещин. 1. С целью избавления появления трещин. 2. Для определения необходимости проверки по раскрытию трещин. 3. Для выявления случая расчета по деформациям. 4. Для проверки появления трещин в сжатой части сечения в период предварительного обжатия бетона. Образование нормальных трещин в центрально-растянутых элементах. Усилие N_crc , воспринимаемое нормальным сечением перед образованием трещин определяется усилием равновесия действующих усилий на продольную ось элемента. Для элементов без предварительного обжатия данное усилие определяется: N_crc= R_вt.ser*А_в+ δ_s*А_s= R_вt.ser*А_в+2*α* R_вt.ser*А_s ; E_s=E_в ; δ_s/ E_s= R_вt.ser/ E_вt.pl= R_вt.ser/λ* E_в=2*R_вt.ser/E_в= δ_s=2*R_вt.ser ; E_s/E_в=2*α*R_вt.ser ; N≤ N_crc

Образование нормальных трещин в изгибаемых и внецентренно сжатых элементах.На образование нормальной трещины не оказывает влияния в изгибающем элементе поперечная сила Q, то работу этих элементов на стадии образования трещин можно считать тождественной или равной. Момент трещинообразования М_crc состоит из момента М₁ –уменьш. Напряжения обжатия бетона в крайнем волокне до 0 и момента М₂ –повыш. Напряжение в том же волокне от 0 до R_вt.ser : М_crc= М₁+ М₂ При действии момента М₁ предполагается упругая работа элемента, тогда М₁= R_вt.ser*W_pl W_pl –упруго-пластический момент сопротивления сечения для крайнего волокна Для определения момента М₂ принимается эпюра нормального напряжения в треугольной сжатой зоне и прямоугольной растянутой зоне бетона, тогда М₂= δ_вр*W_red ; W_red=У_red/у_о ; У_red= У_в+ У_s*α+ У_s´*α ; у_о= S_red/A_red δ_вр –напряжение в бетоне, которое препятствует образованию трещин, т.е. вызванное предварительным обжатием бетона, тогда δ_вр=Р/A_red+Р*l_op/W_red тогда М₂=(Р/A_red+Р*l_op/W_red)* W_red=Р*W_red/A_red+Р_lop=Р(r*l_op)=M_rp r-радиус ядрового сечения.

M_rp –момент усилия обжатия бетона по верхней ядровой точке. Условие определяющее появление трещин: М≤ М_crc= R_вt.ser* W_pl+ M_rp при отсутствии предварительного обжатия M_rp=0 .При внецентренном сжатии момент образования нормальных трещин М_crc определяется без учета неупругих деформаций растянутого бетона, как для сплошного упругого тела и тогда условие определяющее образование трещин будет иметь вид: М≤ М_crc= R_вt.ser* W±N*e_х , знак + принимается , если сила N является сжимающей, а знак - если N растягивающая (внецентренно растянутые элементы) е_х –расстояние от точки приложения силы N до ядровой точки сечения.

32. Расчет ширины раскрытия нормальных трещин в железобетонных элементах. Выполняется по 2 группам пред. состояний от действия нормальных нагрузок, т.е. γ_f=1 ,Ширина раскрытия нормальной трещины а_crc на уровне растянутой арматуры определяется из условия, что сумма удлинение растянутого бетона ∆вt на участке м/д трещинами и ширины раскрытия трещины. а_crc=удлинению арматуры на участке м/д трещинами ∆а_s : ∆а_s=∆вt+ а_crc

Удлинение бетона ∆вt очень малы то ∆вt=0 ; а_crc=∆а_s=E_m*l_s=Ψ_s* E_s*l_s Ψ_s-коэфиц. учитывающий работу бетона на участке м/д трещинами, т.е. в зоне штриховки. а_crc=Ψ_s* E_s*l_s= Ψ_s* Q_s/E_s*l_s ; а_crc=φ₁*φ₂*φ₃* Ψ_s* Q_s/E_s*l_s ; φ₁- коэффициент учитывающий продолжительность действия нагрузки ; φ₂-коэфициент учитывающий профиль продольной арматуры ; φ₃-коэффициент учитывающий характер нагружения (изгибаемый или растянутый элемент) ; Q_s –напряжение в арматуре в сочетании с трещиной. Для ж/б элементов второй категории трещиностойкости ширину раскрытия трещин при непродолжительном действии нагрузки определяют от непродолжительности действия постоянной и длительной нагрузки, а также от действия кратковременных нагрузок. Для элементов третьей категории трещиностойкости ширину непродолжительности раскрытия трещин определяют : а_crc=а_crc1+а_crc2-а_crc3 ; а_crc1- ширина раскрытия трещины от продолжительного действия постоянных и длительных нагрузок ; а_crc2 –ширина раскрытия трещин от непродолжительного действия постоянных и всех временных нагрузок ; а_crc3 –ширина раскрытия трещин от непродолжительного действия постоянных и временных длительных нагрузок. Для уменьшения ширины раскрытия трещин можно уменьшить диаметр арматуры, при этом увеличить её количество, либо применить арматуру периодического профиля.

33. Расчет железобетонных элементов по деформациям (прогибам): общие положения расчета, кривизны и прогибы элементов с трещинами и без трещин. Суть: определение максимального прогиба и сравнение его с предельно допустимым f_ult : f_max≤ f_ult, f_ult –предельно допустимый прогиб, устанавливаемый на основании технологич. Конструкционных и эстетических требований. Определение прогибов для элементов с постоянной жесткостью производится в соответствии зависимости сопротивления материала, поскольку ж/б является анезотропным и неоднородным материалом, то учет теории сопромата выполняется путем введения ряда эмпирических зависимостей. Ж/б балка до образования трещин работает с постоянным сечением и жесткостью =Е_в*У_red

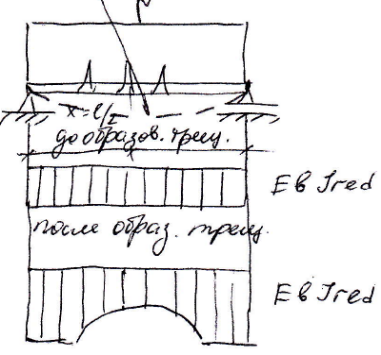После образования трещин жесткость балки в средней части уменьшается. На величину жесткости балки влияют:А, ползучесть бетона, усадка бетона и другие факторы, как трудно учесть при определении жесткости,поэтому рекомендуется вычислять прогибы по кривизнам. Наибольшим удобным является интеграл Мора. f=∫^e_oM_x(1/r)xdx M_x-изгибающий момент в сечении на расстоянии х от опоры, от единичной нагрузки, которая приложена в направлении деформации. (1/r)x-кривизна, в рассматриваемом сечении от нагрузки, при котором определяется прогиб.; r-радиус кривизны. Для элементов постоянного сечения принимаются допущения, что кривизны изменяют пропорцию изгибающему моменту, тогда для однопролетной балки прогиб определяется: f=S*(1/r)max*l² ,S –коэффициент, зависящий от условия опирания и схемы загружения балки. Кривизна и прогиб элемента без трещин. Кривизна изгиба и внецентренно сжатого элемента определяется как для сплошного тела. Полная кривизна: (1/r)= (1/r)₁+(1/r)₂ ; (1/r)₁;(1/r)₂ –кривизна соответственно от непродолжительного действия длительных нагрузок, и от продолжительного действия постоянного и длительных нагрузок. Кривизну ж/б элемета от действия соответствующих нагрузок определяют: (1/r)=М/Д, М–изгибающий момент от внешней нагрузки с учетом момента от продольной силы относительно центра тяжести сечения. Д -изгибная жесткость приведенного поперечного сечения. Д=Е_в1*У_red ; Е_в1-модуль деформации сжатого бетона. При непродолжительном действии нагрузок. Е_в=0,85* Е_в ,При продолжительном нагрузок : Е_в1= Е_в/1+φ_в,сr ; φ_в,сr-коэффициент ползучести. У_red= У_в+α*У_s+У_s^´ ; α=Е_s/ Е_в1 Кривизна и прогиб элемента с трещинами. Полная кривизна определяется по формуле: (1/r)=(1/r)₁+(1/r)₂+(1/r)₃ ; (1/r)₁-кривизна от непродолжительного действия всей нагрузки ; (1/r)₂-кривизна от непродолжительного действия постоянных и длительных нагрузок ; (1/r)₃-кривизна от продолжительного действия постоянных и длительных нагрузок. Кривизна определяется от действия соответствующих нагрузок по формуле: (1/r)=М/Д ; Д=Е_s,_red ; А_s=(h_o-x_m) Е_s,_red-приведенный модуль деформации растянутой арматуры, определяемый с учетом влияния работы растянутого бетона м/д трещинами Е_s,_red=E_s/Ψ_s ,Z-расстояние от центра тяжести растянутой арматуры до точки приложения равнодействующей усилий в сжатой зоне. x_m-высота сжатой зоны сечения.