4.2. Классический метод расчёта переходных процессов

Классический метод расчета переходных процессов основан на составлении и последующем решении (интегрировании) дифференциальных уравнений, составленных по законам Кирхгофа и связывающих искомые токи и напряжения послекоммутационной цепи и заданные воздействующие функции (источники электрической энергии. Преобразуя систему уравнений, можно вывести итоговое дифференциальное уравнение относительно какой-либо одной переменной величины x(t):

. (4.2)

Здесь n – порядок дифференциального уравнения, он же – порядок цепи, коэффициенты a_k > 0 и определяются параметрами пассивных элементов R, L, C цепи, а правая часть является функцией задающих воздействий.

В соответствии с классической теорией дифференциальных уравнений полное решение неоднородного дифференциального уравнения находится в виде суммы частного решения неоднородного дифференциального уравнения и общего решения однородного дифференциального уравнения:

. (4.3)

Частное решение полностью определяется видом правой части f(t) дифференциального уравнения. В электротехнических задачах правая часть зависит от воздействующих источников электрической энергии, поэтому вид обуславливается (принуждается) источниками электрической энергии и называетсяпринужденной составляющей .

Общее решение однородного дифференциального уравнения зависит от корней характеристического уравнения, которые определяются коэффициентами дифференциального уравнения, и не зависит от правой части. В прикладных задачах электротехники не зависит (свободно) от воздействующих источников и по этой причине называетсясвободной составляющей и полностью определяется параметрами пассивных элементов цепи, а физически процессом перераспределения запасов энергии электрического и магнитного полей в реактивных элементах цепи.

Таким образом, любая искомая величина в переходном режиме

. (4.3)

Свободную составляющую переходного процесса ищут в виде

,(4.4)

где n – порядок цепи, совпадающий с порядком дифференциального уравнения;

p_k – корни характеристического уравнения (собственные числа цепи);

A_k – постоянные интегрирования.

Собственные числа линейных цепей либо действительные отрицательные, либо комплексные с отрицательными вещественными частями (т.е. находятся в левой полуплоскости комплексных чисел). Поэтому носит преходящий (асимптотически затухающий до нуля) характер.

В искомом решении надо уметь определять величины,n, p_k, A_k.

4.2.1. Определение принужденной составляющей

Уравнение (4.3) при принимает вид, т.к. затухает до пренебрежимо малых размеров. Эти соображения позволяют утверждать:принужденная составляющая переходного процесса совпадает с соответствующей величиной в послекоммутационном установившемся режиме и может быть получена изученными ранее методами.

Электрическая цепь для расчета принужденных составляющих от источников постоянных воздействий должна быть чисто резистивной (индуктивности заменяются короткозамкнутыми участками, а емкости – разомкнутыми). При наличии источников с гармоническими воздействиями расчет принужденных составляющих ведется символическим методом.

4.2.2. Определение порядка цепи n

В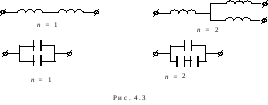простейших случаях низкопорядковых цепей можно руководствоваться следующей рекомендацией:порядок цепи определяется количеством независимых реактивных элементов в этой цепи, другими словами,количеством независимых начальных условий. Так, например, фрагменты цепей, приведенных на рис. 4.2, дают вклад в величинуn:

В случае большого количества реактивных элементов в цепи порядок определяется оценочными формулами. Не претендуя на полноту изложения, в качестве примера приведем одну из них:

(4.5)

где r– число реактивных элементов;

а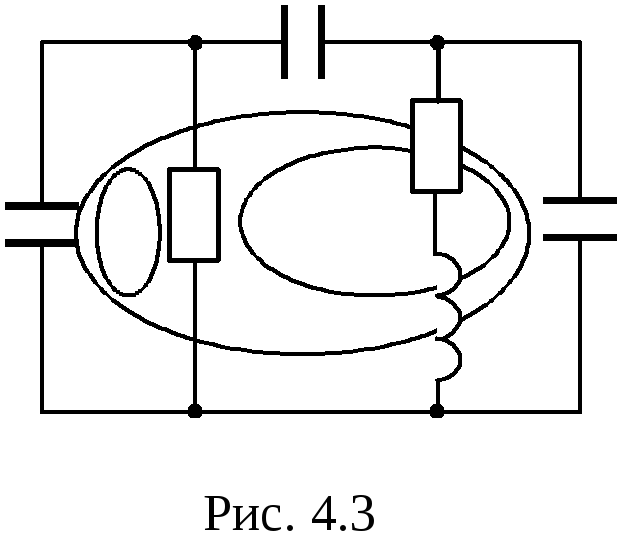_L, a_C– число узлов, связывающих только индуктивные, или только ёмкостные токи соответственно;

b_L, b_C – число контуров, проходящих только через реактивные элементы – индуктивности и ёмкости, соответственно, и не содержащие резисторов.

Рассмотрим применение формулы (4.5) на примере схемы (рис. 4.3): r = 4, a_L = 0, a_C = 0, b_L = 0, b_C = 1, следовательно, порядок цепиn = 4 – 1 = 3.

Часто к быстрому результату при определении порядка цепи приводит следующая рекомендация: степень характеристического уравнения равна сумме порядков дифференциальных уравнений для независимых контуров, выбранных так, чтобы порядок дифференциальных уравнений для них был наименьшим.

Так цепь на рис. 4.3 имеет три независимых контура: внешний контур имеет нулевой порядок, левая ячейка-контур – первый порядок и любой из оставшихся контуров (средняя ячейка, например) – второй порядок. Суммируя порядки этих контуров, получаем n = 3.