
Пермский Государственный Технический Университет
Кафедра “Конструирование радиоэлектронных средств”
Отчет по лабораторной работе № 4:
“Исследование резонансных явлений
в последовательной цепи RLC”
Выполнили студенты гр. АТПП-02-2:
Цидвинцев Денис
Мартынов Михаил
Проверил:
Кулютникова Е.А.
Пермь 2003
Цель работы: исследовать реакцию колебательного контура из последовательно соединенных элементов RLC на изменение частоты приложенного напряжения, неизменного по величине, получить навыки экспериментального исследования резонансных и частотных характеристик; закрепить и расширить знания о резонансе.
Схема:

Таблица:
|
f, кГц |
Измерено |
Вычислено |
||||||||
|
Uвх, В |
I, мА |
Uc, В |
Uк В |
UL, В |
XL, Ом |
XC, Ом |
Z, Ом |
XЭ, Ом |
φ, гр |
|
|
1 |
10 |
0,32 |
11,24 |
0,55 |
0,49 |
1531 |
35125 |
33610 |
-33594 |
-88,2 |
|
2 |
0,73 |
13,05 |
2,41 |
2,34 |
3205 |
17876 |
14707 |
-14671 |
-85,9 |
|
|
3 |
1,47 |
17,95 |
7,44 |
7,35 |
5000 |
12210 |
7284 |
-7210 |
-81,8 |
|
|
4 |
3,74 |
34,9 |
26,3 |
26,13 |
6986 |
9331 |
2532 |
-2342 |
-66,1 |
|
|
5 |
5,36 |
36,4 |
42,9 |
42,69 |
7964 |
6791 |
1567 |
1173 |
48,5 |
|
|
6 |
2,35 |
13,5 |
23,4 |
23,33 |
9927 |
5744 |
4310 |
4183 |
76,0 |
|
|
7 |
1,43 |
7,31 |
17,5 |
17,46 |
12209 |
5111 |
7173 |
7098 |
81,7 |
|
|
8 |
1,04 |
4,72 |
15,0 |
14,98 |
14403 |
4538 |
9919 |
9865 |
83,9 |
|
|
9 |
0,81 |
3,3 |
13,6 |
13,58 |
16765 |
4074 |
12733 |
12691 |
85,3 |
|
|
10 |
0,65 |
2,43 |
12,7 |
12,69 |
19523 |
3738 |
15819 |
15785 |
86,2 |
|
|
f0 |
9,62 |
52,3 |
51,9 |
51,34 |
5337 |
5436 |
1044 |
-99 |
-0,1 |
|
f0=4,55 кГц;
R=R1+R2=250 Ом;
RЭ=Uвх/I0, где I0 - резонансный ток, а RЭ - активное сопротивление всей цепи;
RЭ=1039,5 Ом;
RK= RЭ-(R1+R2)=789,5 Ом.
UL, XL, XC, Z, определяются по формулам:
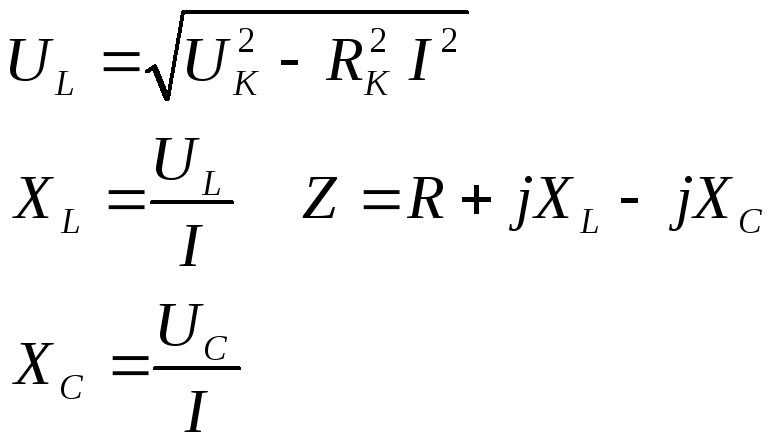
 Z=R2+XЭ2;
=arctg(XЭ/RЭ).
Z=R2+XЭ2;
=arctg(XЭ/RЭ).
Векторные диаграммы в масштабе для частот f=3кГц, f=8кГц, f=f0.
|
f=3 кГц; UR=0,006 B; URL=0,002 B. |
f=8 кГц; UR=0,004 B; URL=0,001 B. |
|
U
Uвх
UC |
UC
Uвх
|
f=8 кГц; UR=0,038 B; URL=0,012 B.
 UR URL
UR URL


 I
I
Uвх UL
UC
Резонансные UL(f), UC(f), I(f) и частотные XL(f), XC(f), Z(f), XЭ(f), (f) характеристики.
UC(f), UL(f)(штриховая):
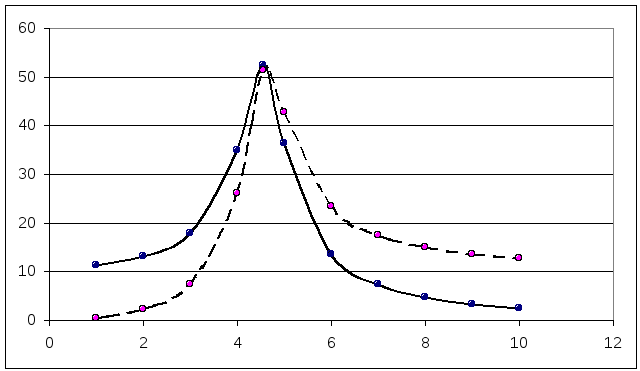
I(f):
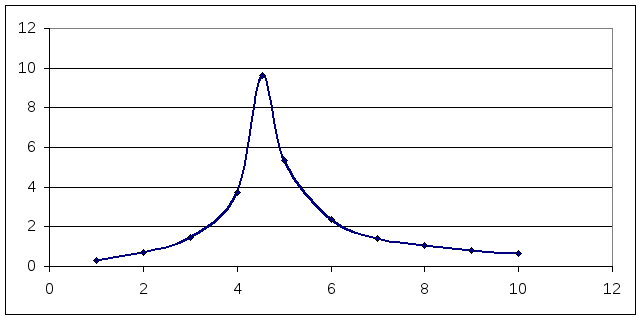
XL(f), XC(f)(штриховая), Z(f)(штрих-пунктирная):
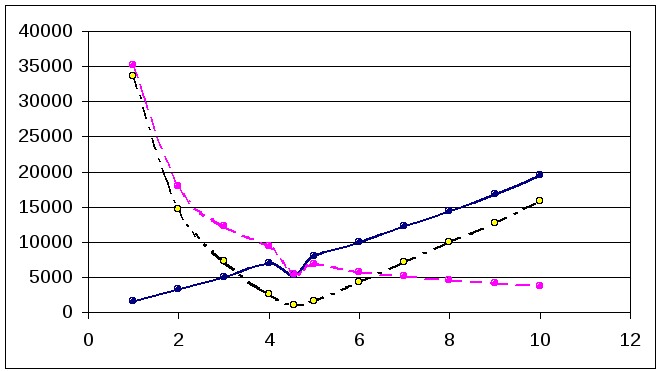
XЭ(f):
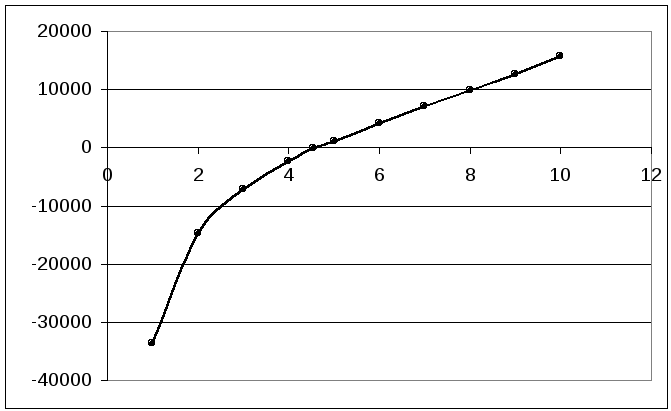
(f):
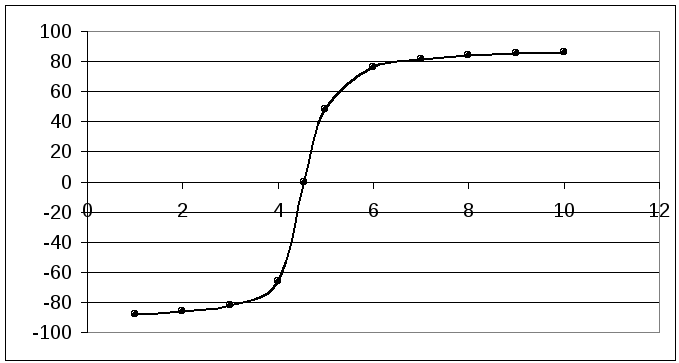
Добротность:
Q=UL/UВХ=UC/UВ5,2,
где UL и UC – напряжения при резонансе.
Полосы пропускания:
fниж=4,16 кГц;
fверх=5,04 кГц.
Контрольные вопросы:
-
Каковы условия резонанса напряжения и резонансная частота последовательной цепи RLC, если в ней зашунтировать резистором:
a) индуктивность L в этой цепи;
б) емкость С?
-
Как влияет шунтирование элементов L и С резистором на величину резонансной частоты?
-
Вычертить векторные диаграммы для схем в вопросе 1.
-
При каких условиях напряжение на реактивных элементах L, С при последовательном их соединении может превысить входное напряжение схемы UВХ?
-
Какими величинами характеризуются резонансные свойства контура RLC?
-
Что нужно сделать, чтобы улучшить резонансные свойства исследуемой цепи?
Ответы на контрольные вопросы:
1. а)
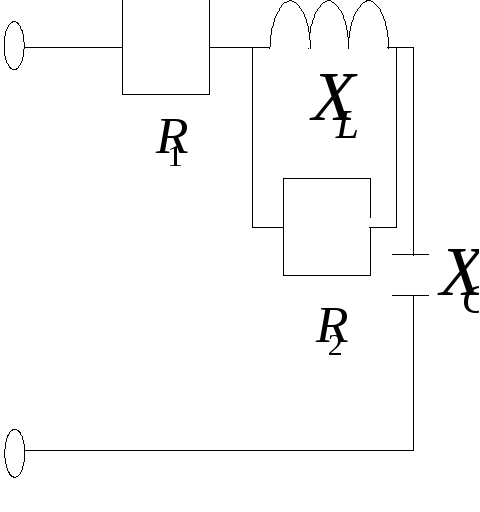
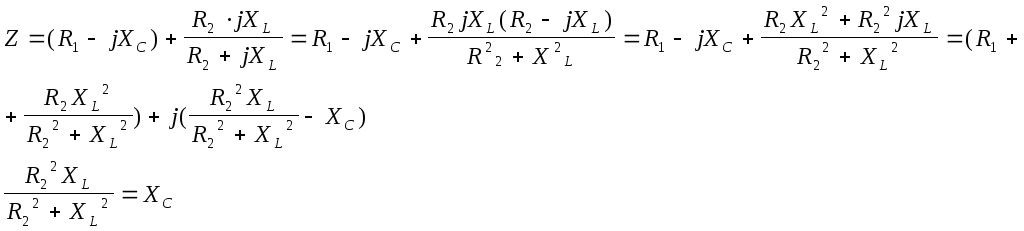
б)
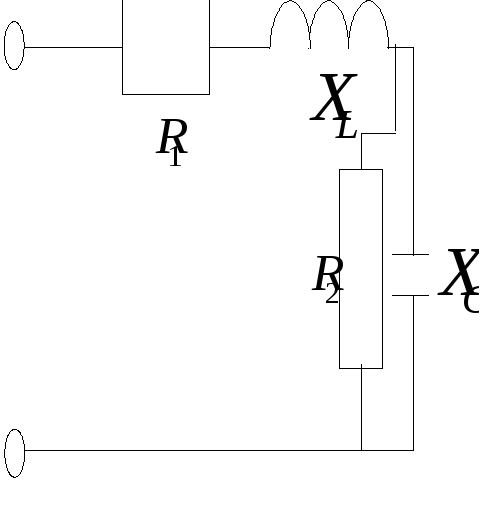
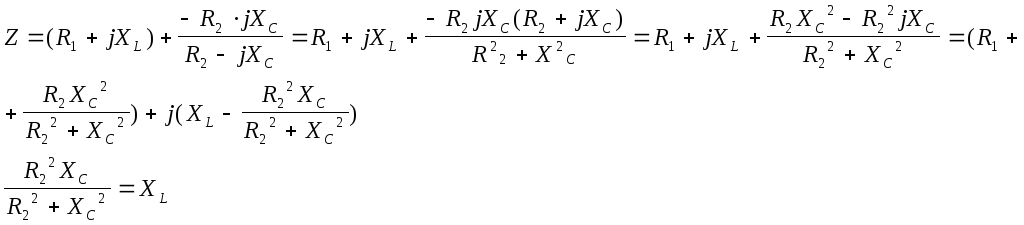
2. а)
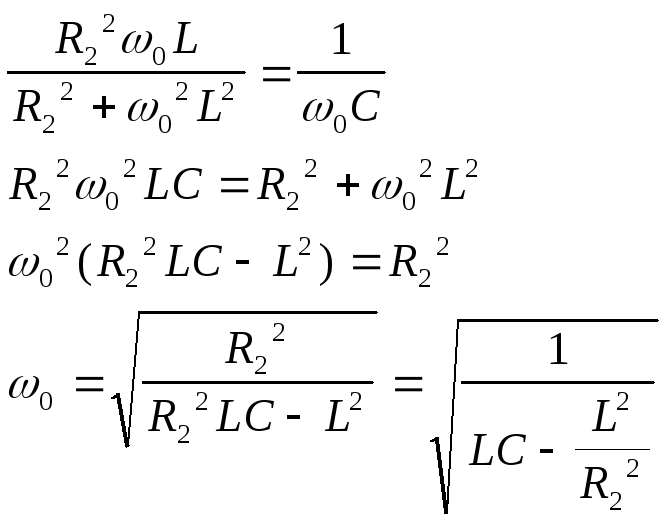
При
шунтировании L
резистором резонансная частота
увеличилась, т.к. уменьшается знаменатель
на
![]()
б)
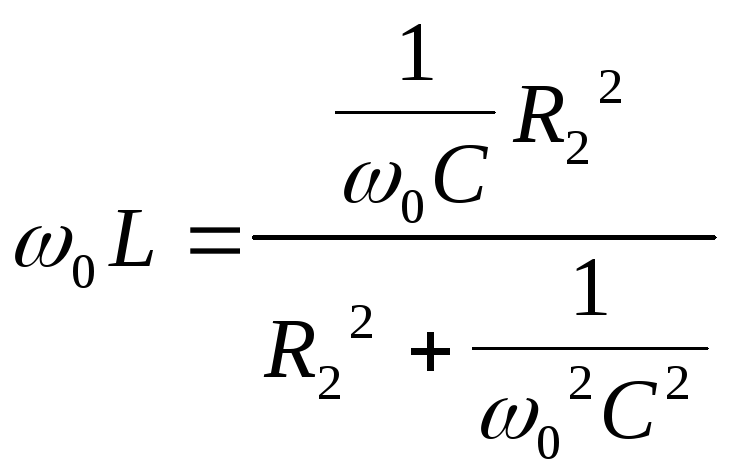
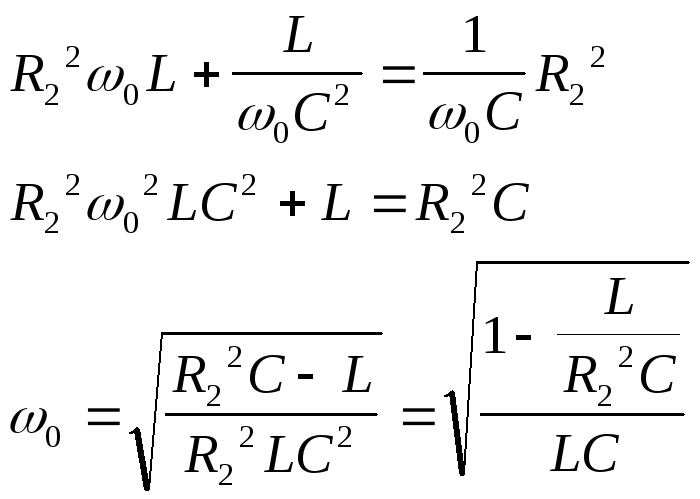
При
шунтировании C
резистором резонансная частота
уменьшилась, т.к. увеличился числитель
на
![]()
3. Векторная диаграмма для вопроса 1
а)
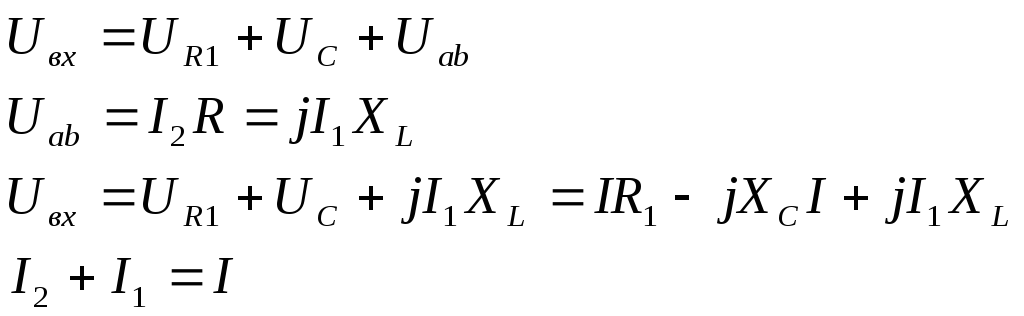
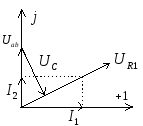
б)
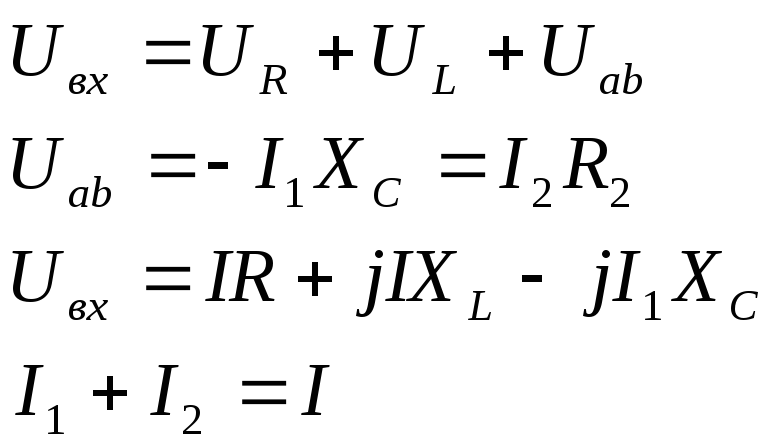
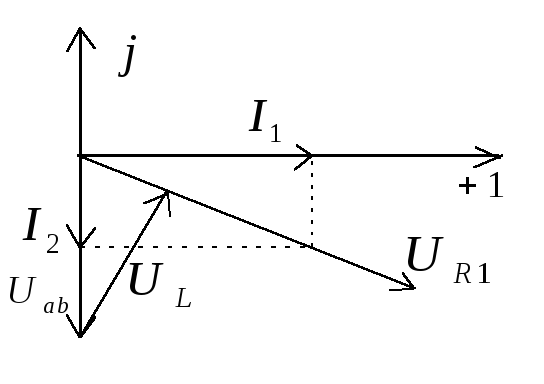
4.
Напряжение
на L
и C
может превысить входное![]() (при их последовательном соединении) в
случае резонанса напряжений
(при их последовательном соединении) в
случае резонанса напряжений
![]() т.е.
т.е.
![]() ,
т.е.
,
т.е.
![]()
5.
Резонанс
свойства контура характеризуется
добротностью
![]() и полосой пропускания
и полосой пропускания
![]()
6.
Чтобы улучшить
резонансные свойства контура необходимо
уменьшить активное сопротивление
контура
![]() увеличивается
добротность контура. Также можно изменить
индуктивность или емкость.
увеличивается
добротность контура. Также можно изменить
индуктивность или емкость.
7. Графики UL(L), UC(L), I(L) и UL(C), UC(C), I(C) в последовательной цепи RLC:
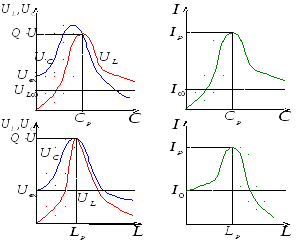
Пояснение к приведенным графикам:
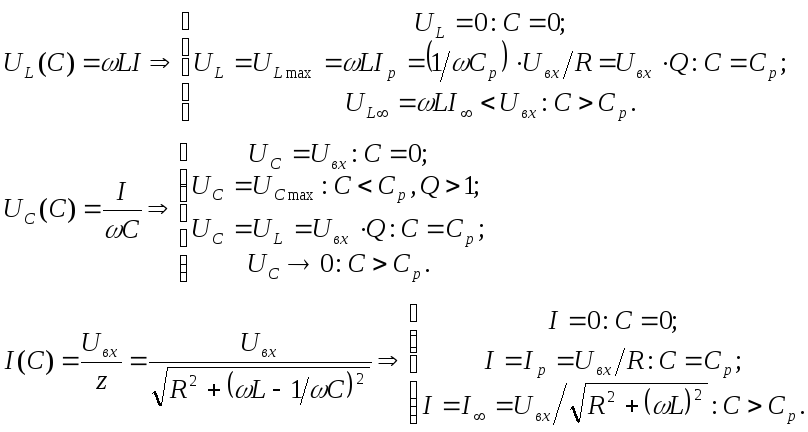

 R I
R I
 U
U L URL
L URL
 UL
UL
 URL
URL
 UR I
UR I