6. Расчет трехфазных цепей

Рассмотрим расчет трехфазной цепи звезда – звезда с нейтральным проводом (рис. 1.7). Расчет такой цепи можно производить всеми известными методами расчета разветвленных цепей. Чаще всего рационально применять метод узловых потенциалов, т.к. в этой схеме два узла O и O₁, и для определения неизвестных токов и напряжений нужно составить одно уравнение. Примем потенциал точкиОравным нулю, тогда напряжение нейтрали

. (1.8)

Здесь

– комплексы ЭДС соответствующих фаз генератора,;

– комплексные проводимости соответствующих фаз нагрузки и нулевого провода.

Напряжение на фазах нагрузки

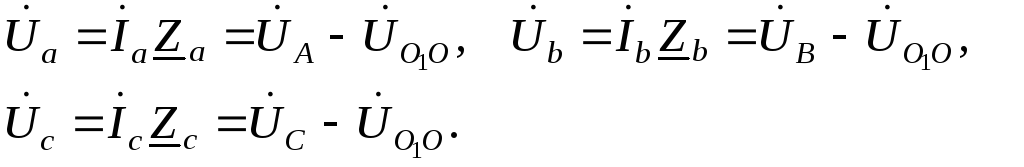(1.9)

Токи в фазах:

(1.10)

Рассмотрим несколько частных случаев.

1. Отсутствует сопротивление в нейтральном проводе 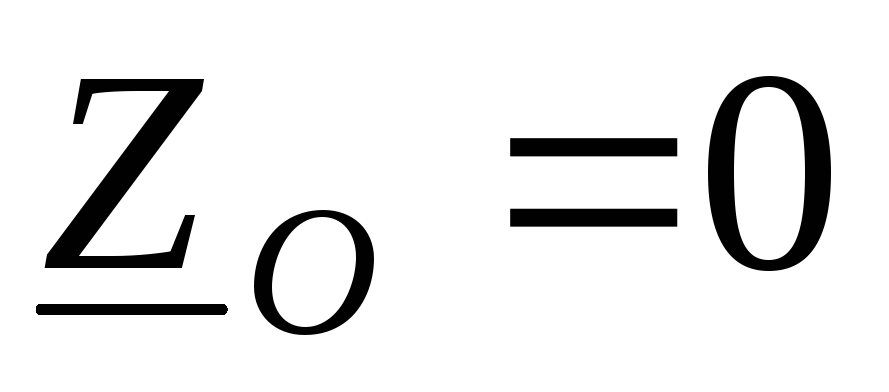, тогда.

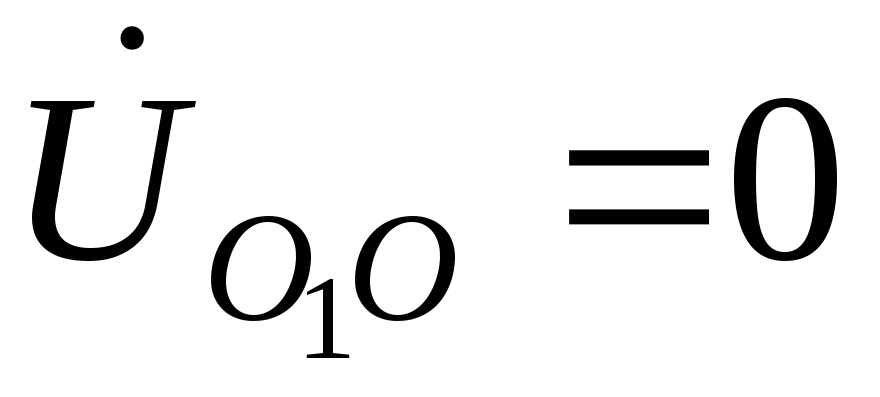2. Сопротивления нагрузки одинаковы 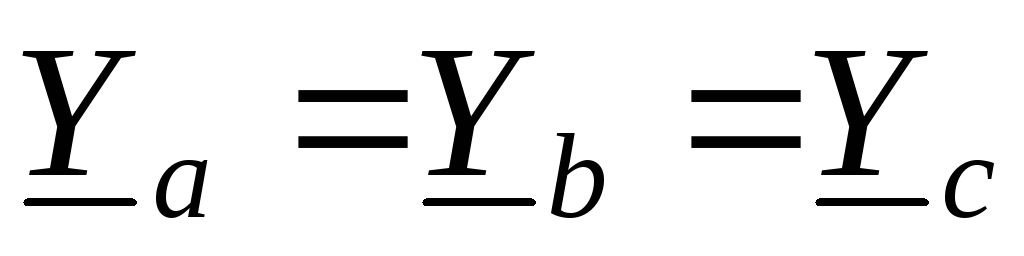, нагрузка симметрична. Из (1.8) следует, что в этом случае также напряжение нейтрали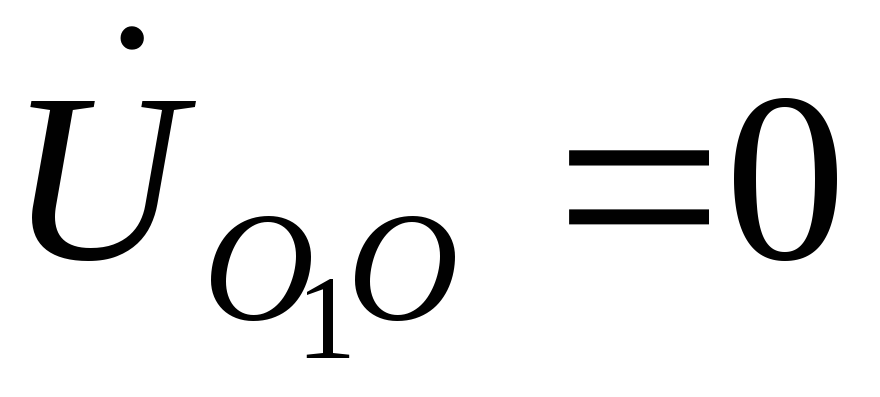. Линейные токи соответственно равны

(1.11)

Учитывая соотношение (1.11), векторные диаграммы напряжений на нагрузке и на генераторе совпадают и имеют вид, представленный на рис. 1.8, а.

П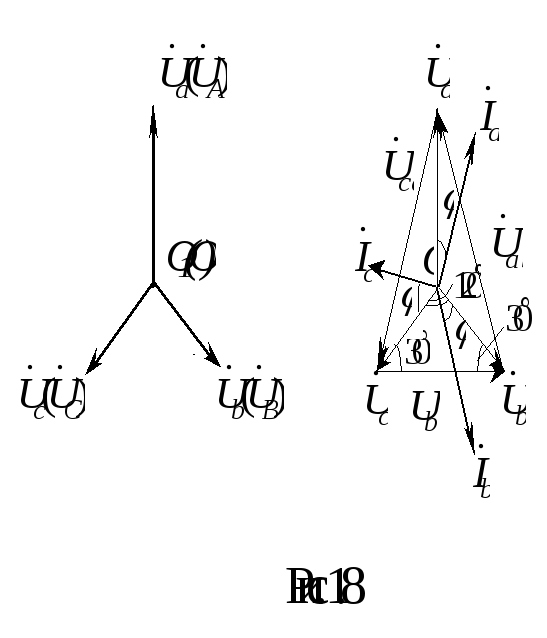ри активно-индуктивном характере нагрузки > 0, векторные диаграммы токов и напряжений на нагрузке показаны на рис. 1.8, б. Учитывая соотношения между фазными и линейными напряжениями, получим, соединяя соответствующие точкиa сb, b с c, c сa, линейные напряжения. Из диаграмм на рис. 1.8 очевидно, что модули всех линейных напряжений равны.

Рассчитав треугольник, образованный, например, фазными напряжениями и линейным, получим

. (1.12)

Здесь – модули фазного напряжения симметричной нагрузки.

3. Нейтральный провод отсутствует, что соответствует схеме «звезда – звезда без нейтрального провода». Расчет производится по формулам (1.8, 1.9) с учетом того, что .

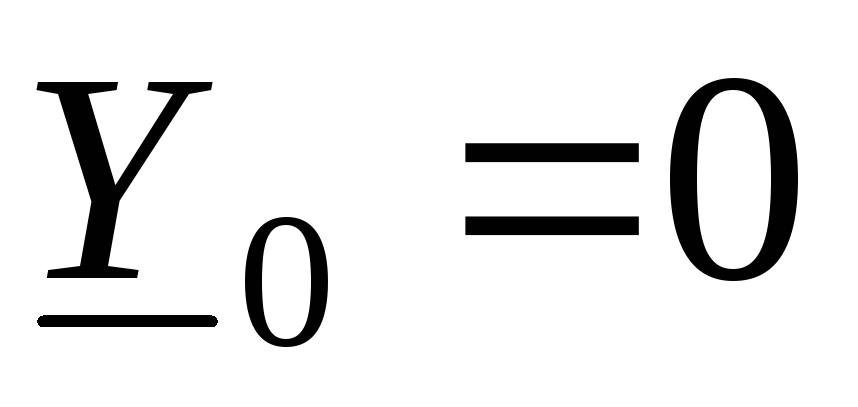Замечание. В схеме «звезда – звезда без нейтрального провода» с симметричным генератором и несимметричной нагрузкой в случае равенства комплексных сопротивлений только в двух фазах напряжение нейтрали можно определить из соотношений

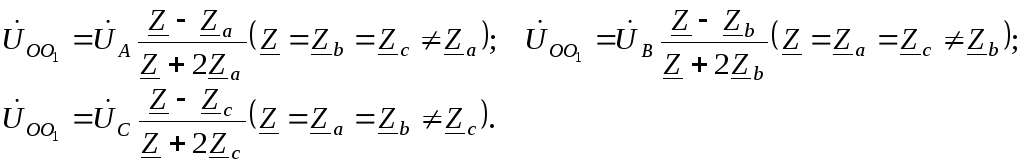
Покажем справедливость этих формул на примере .

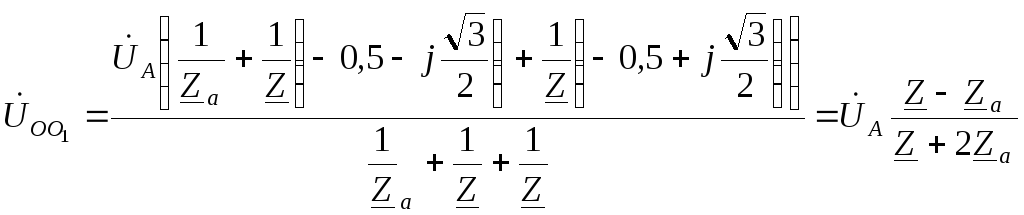
При соединении нагрузки в треугольник токи в его фазах определяются по закону Ома

. (1.13)

Линейные токи находят по первому закону Кирхгофа

. (1.14)

П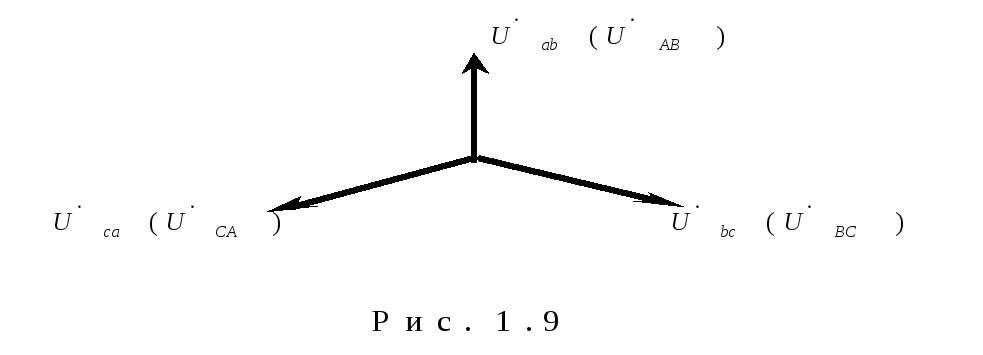оскольку линейные напряжения на нагрузке равны линейным напряжениям на генераторе, которые в свою очередь равны соответствующим ЭДС на обмотках генератора, векторная диаграмма линейных напряжений на нагрузке (рис. 1.9) полностью совпадает с векторной диаграммой генераторных ЭДС, приведенных на рис. 1.2.

П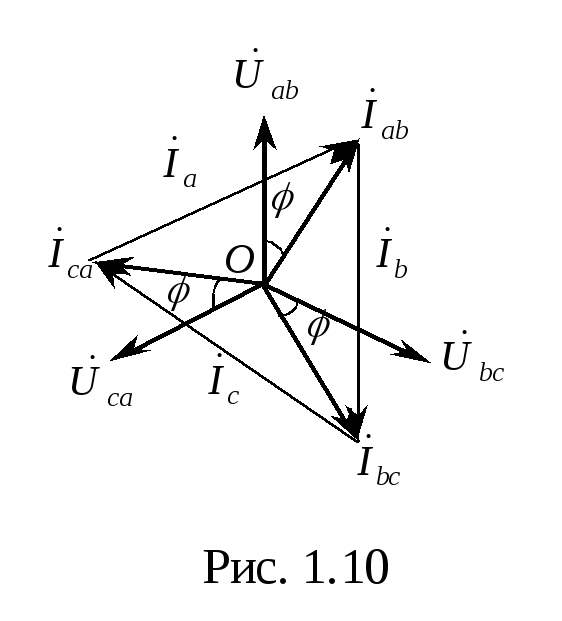усть нагрузка симметрична и носит активно-индуктивный характер, тогда векторные диаграммы напряжений, фазных и линейных токов имеют вид, представленный на рис. 1.10. С помощью полученной диаграммы можно определить, что модули линейных токов равны (они являются сторонами равностороннего треугольника)

.

Из расчета треугольников, образованных двумя фазными токами (биссектрисы равностороннего треугольника) и линейным током, следует, что

. (1.15)

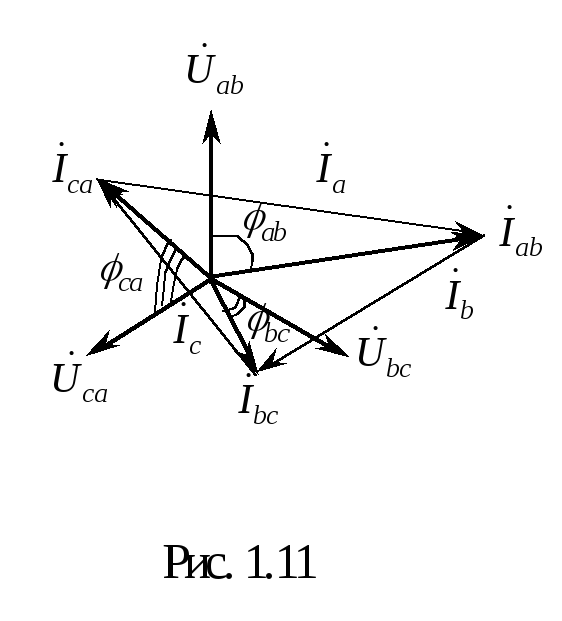
При несимметричной нагрузке векторные диаграммы токов имеют самый разнообразный вид. Пример такой диаграммы приведен на рис. 1.11, где .

3-4. Некоторые частные режимы работы трехфазных цепей

Р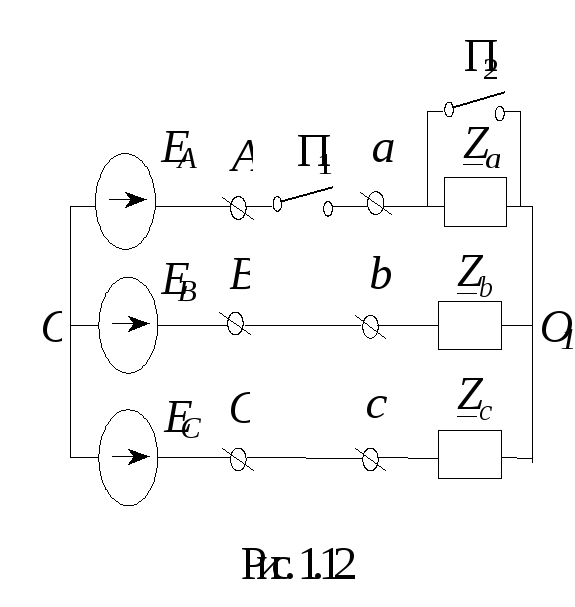ассмотрим частные режимы работы трехфазных цепей на примере соединения «звезда – звезда» и соединения нагрузки в треугольник.

Рассмотрим три режима работы схемы, представленной на рис. 1.12.

1. , переключатель П₁замкнут, переключатель П₂разомкнут. Имеет место симметричный режим работы трехфазной цепи

,

по величине .

В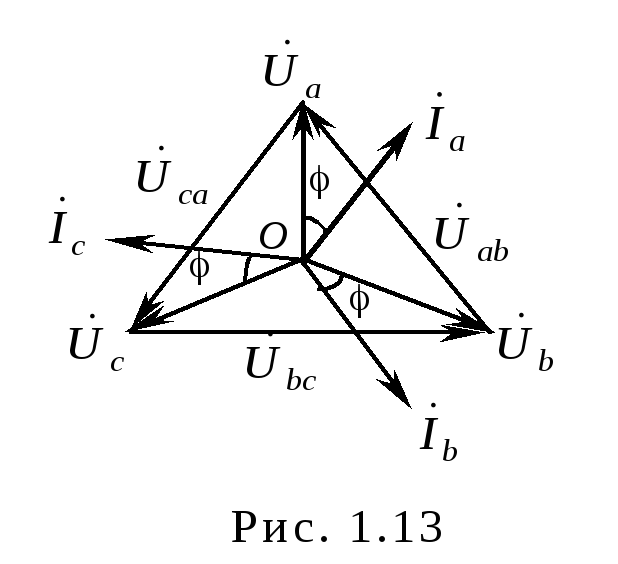екторные диаграммы при активно-индуктивной нагрузке представлены на рис. 1.13. Все фазные токисмещены относительно соответствующих фазных напряжений на угол. Линейные напряжения опережают фазные напряжения на 30(

).

2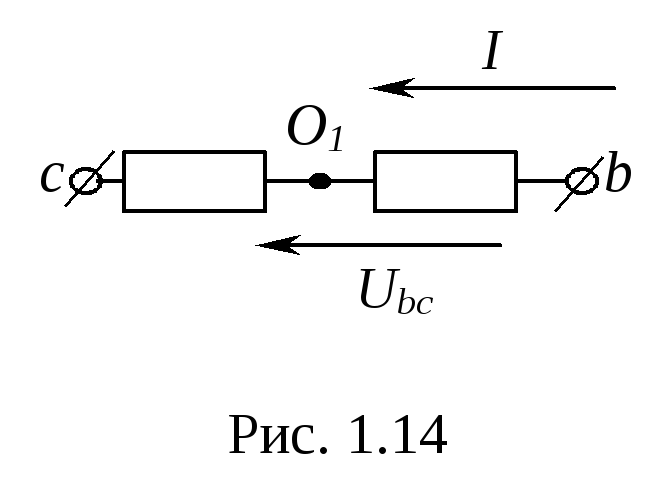. Переключатели П₁и П₂разомкнуты (режим холостого хода илиобрыв фазыА). При этом схема из трехфазной цепи преобразуется в однофазную с напряжениемна сопротивлениях(рис. 1.14). Потенциал точкиО₁становится равным.

Векторные диаграммы представлены на рис. 1.15.

Ток в сопротивлениях иравен.

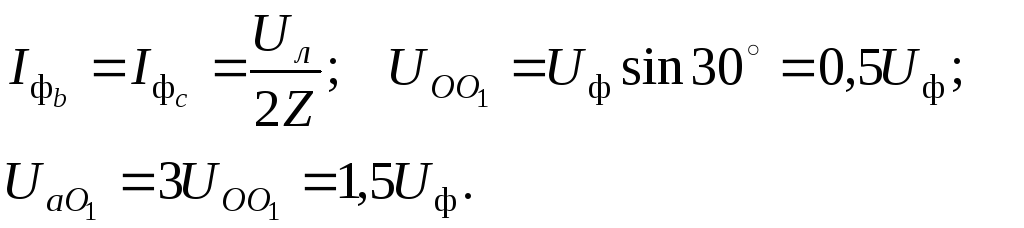
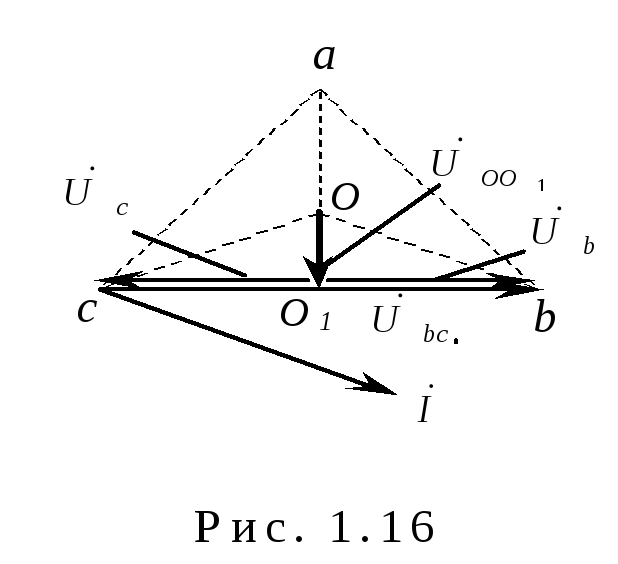
Таким образом, фазный ток и фазное напряжение неповрежденных фаз уменьшилось в раза.

3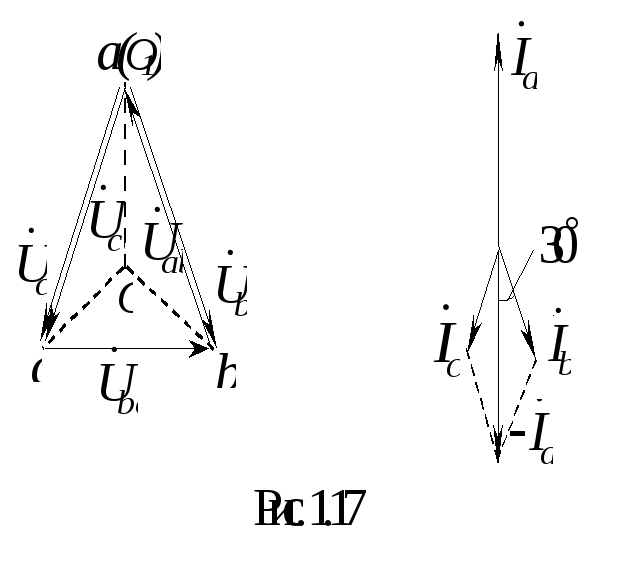. Переключатели П₁и П₂замкнуты (режим короткого замыкания фазыА). Потенциал точкиО₁ принимает значение потенциала точкиa. Векторные диаграммы представлены на рис. 1.17.

В этом режиме .

.

Таким образом, фазные напряжения и токи неповрежденных фаз B иC увеличились враз, а ток закороченной фазы (I_a) – в 3 раза по сравнению с симметричным режимом работы схемы.

Н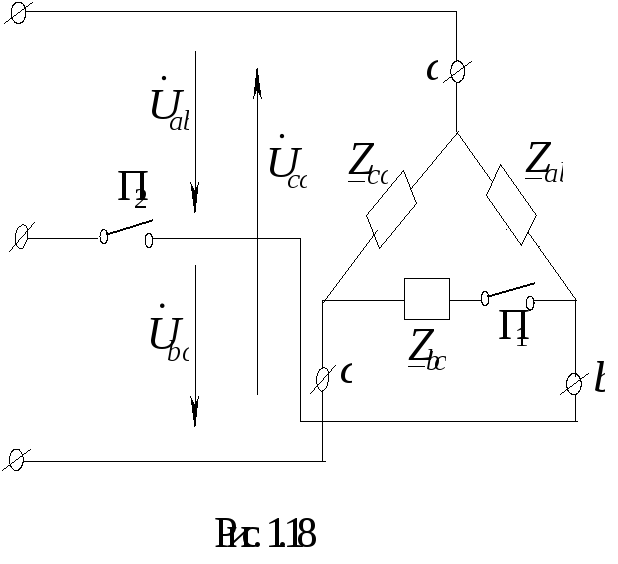а рис. 1.18 приведена схема, состоящая из трех одинаковых сопротивлений, соединенных треугольником, которые подключены к симметричной системе линейных напряжений. Рассмотрим три режима работы этой схемы.

1. Переключатели П₁и П₂замкнуты. При этом имеет местосимметричный режимработы трехфазной цепи.

(1.16)

В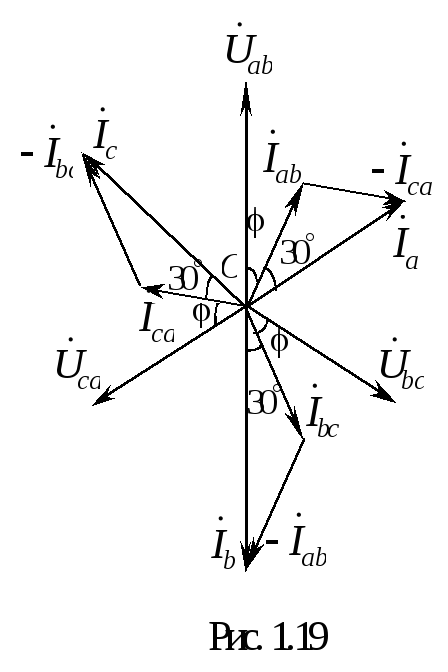екторные диаграммы напряжений и токов при активно-индуктивной нагрузке приведены на рис. 1.19.

Все фазные токи отстают от соответствующих фазных напряженийна угол. Линейные токиотстают от соответствующих фазных токовна 30.

(1.17)

2. Переключатель П₁разомкнут (режим холостого хода илиобрыв фазыbc).

(1.18)

Л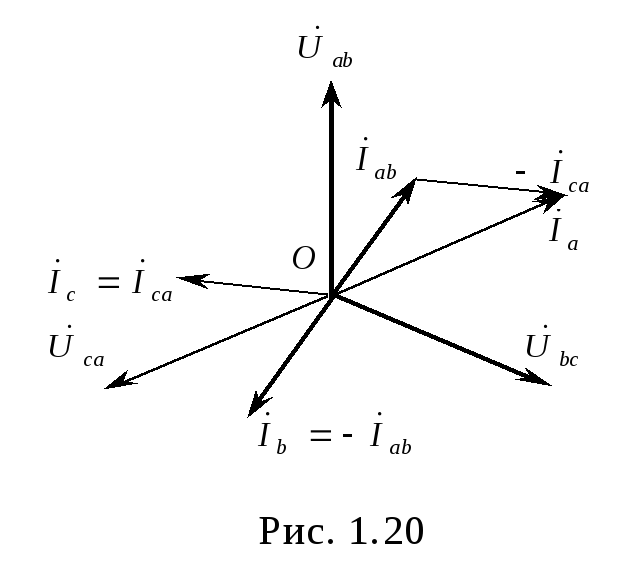инейные токи, т.е.. Таким образом, линейный ток в проводе, не связанном гальванически с «поврежденной» фазой, остается неизменным по сравнению с симметричным режимом, а два других линейных токаистановятся равными фазным токам при симметричном режиме. Векторные диаграммы напряжений и токов приведены на рис. 1.20.

3. Переключатель П₁ замкнут, а переключатель П₂разомкнут (обрыв линии В). При этом трехфазная цепь преобразуется в однофазную, и все три сопротивления подключаются к напряжению(рис. 1.21). Векторные диаграммы напряжений и токов для этой схемы представлены на рис. 1.22.

Т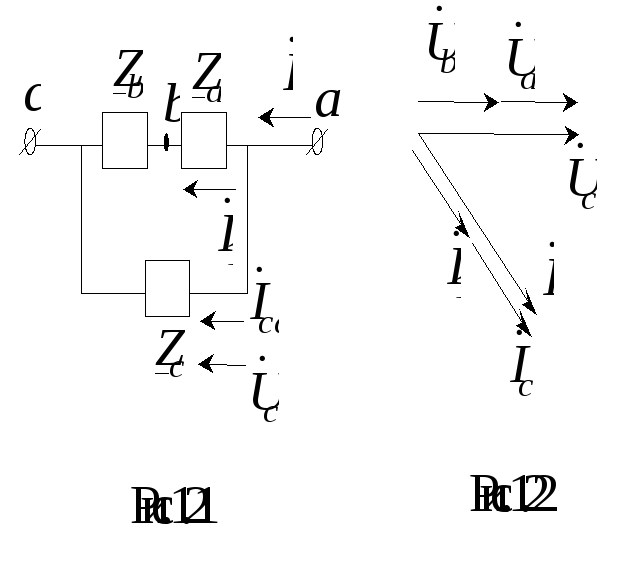ок, протекающий по двум сопротивлениями, ток в фазеca. Линейные токи.

Таким образом, при обрыве линейного провода в фазах, гальванически связанных с ним, токи уменьшаются в два раза, в третьей фазе ток остается неизменным, линейный ток в неповрежденной линии уменьшается по сравнению с симметричным режимом в 1,15 раза.