36. Определение постоянных интегрирования
Как известно, постоянные интегрирования определяются из начальных условий, каковыми являются значения искомой функции и ее производных по (n– 1)-ую включительно в начальный момент времени 0+(«справа»). В отличие от чисто математических задач, где эти условия задаются в качестве исходных данных непосредственно, при анализе переходных процессов задаются начальные условия «слева» в моментt = 0–, предшествующий коммутации (чаще всего они формулируются самой постановкой задачи и легко определяются из расчета докоммутационного режима). Нахождение начальных условий «справа» по известным значениям начальных условий «слева» – ключевой момент в расчете переходных процессов.
Опишем процедуру отыскания начальных условий в цепи n-го порядка
для послекоммутационной схемы (
)
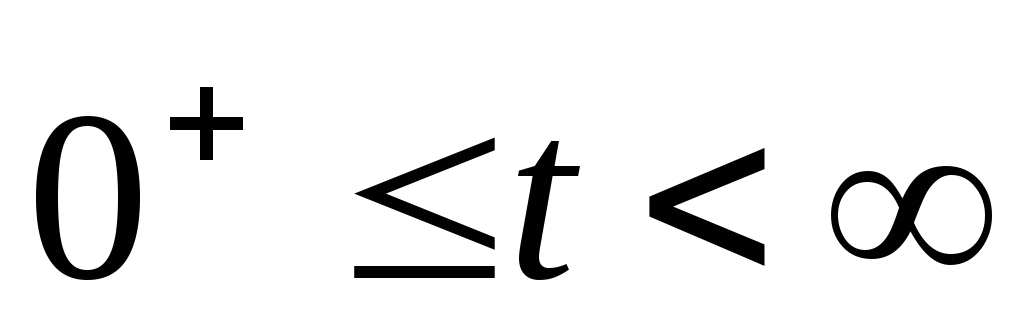составляют систему уравнений для
мгновенных значений токов и напряжений
по законам Кирхгофа, дополняют эту
систему компонентными уравнениями
типа
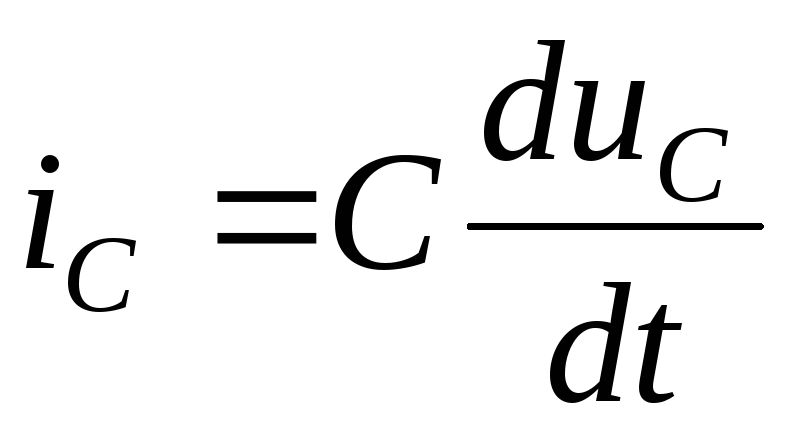для емкости;рассматривают эту систему уравнений в момент t = 0+с учетом независимых начальных условий, которые по правилам коммутации берутся равными начальным условиям «слева», в результате определяются зависимые начальные условия, в том числе значения первых производных от индуктивных токов и емкостных напряжений;
для отыскания значений первых производных от зависимых электрических величин и вторых производных от независимых электрических величин необходимо систему уравнений из п. 1 продифференцировать и рассмотреть ее в момент t = 0+ с учетом информации, полученной в п. 2;
процедура дифференцирования продолжается до тех пор, пока не будет найдена (n– 1)-ая производная искомой функции в 0+.
Система уравнений для определения постоянных интегрирования имеет следующий вид:
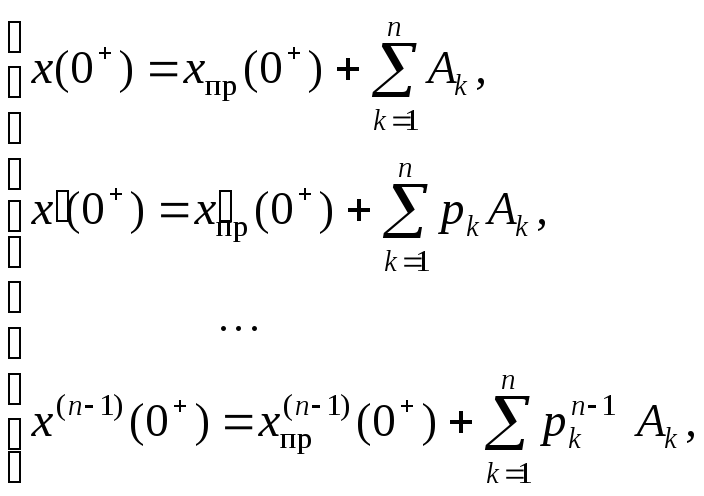(4.9)
Здесь для определенности полагаем все корни pk вещественными разными числами. Кроме того, следует учитывать, что при наличии в цепи только источников постоянных воздействий значение производных от принужденной составляющей переходного процесса равны нулю.
Возможная схемная реализация этой технологии подробно описана в [] и позже будет пояснена на конкретном примере.
37. Определение порядка цепи n
В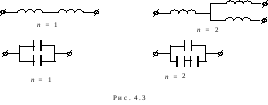
простейших случаях низкопорядковых
цепей можно руководствоваться следующей
рекомендацией:порядок
цепи определяется количеством независимых
реактивных элементов в этой цепи, другими
словами, количеством
независимых начальных условий.
Так, например, фрагменты цепей, приведенных
на рис. 4.2, дают вклад в величину n:
В случае большого количества реактивных элементов в цепи порядок определяется оценочными формулами. Не претендуя на полноту изложения, в качестве примера приведем одну из них:
(4.5)
где r– число реактивных элементов;
а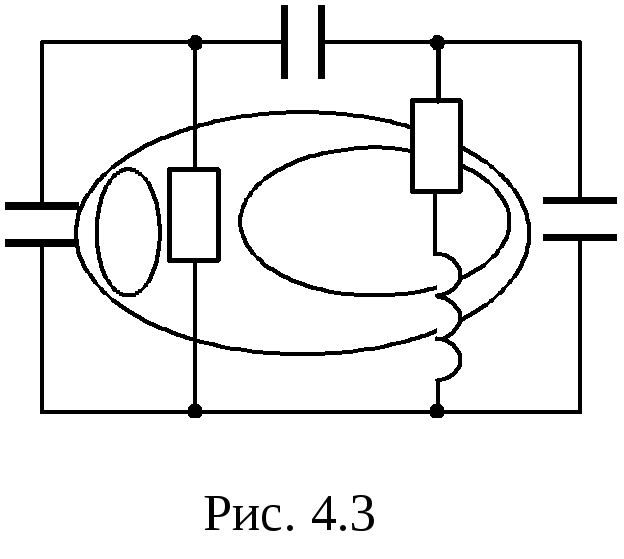
L,
aC– число узлов, связывающих только
индуктивные, или только ёмкостные токи
соответственно;
bL, bC– число контуров, проходящих только через реактивные элементы – индуктивности и ёмкости, соответственно, и не содержащие резисторов.
Рассмотрим применение формулы (4.5) на примере схемы (рис. 4.3): r = 4,aL = 0,aC = 0,bL = 0,bC = 1, следовательно, порядок цепиn = 4 – 1 = 3.
Часто к быстрому результату при определении порядка цепи приводит следующая рекомендация: степень характеристического уравнения равна сумме порядков дифференциальных уравнений для независимых контуров, выбранных так, чтобы порядок дифференциальных уравнений для них был наименьшим.
Так цепь на рис. 4.3 имеет три независимых контура: внешний контур имеет нулевой порядок, левая ячейка-контур – первый порядок и любой из оставшихся контуров (средняя ячейка, например) – второй порядок. Суммируя порядки этих контуров, получаем n = 3.