Тест 300 вопросов математика

1. Дана матрица . Найти определитель матрицы В = АА’

а) 9;

б) 12

с) 0

2. Найти след t_r C матрицы

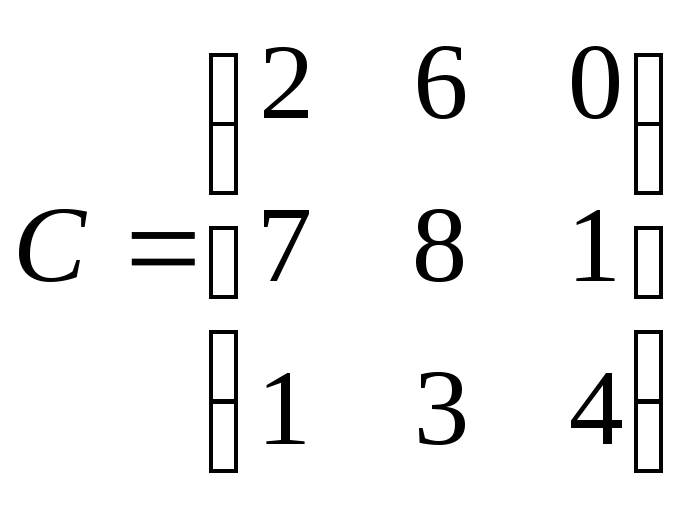
а) 14

б) 9

с) 17

3. Сколько линейно независимых строк имеет матрица

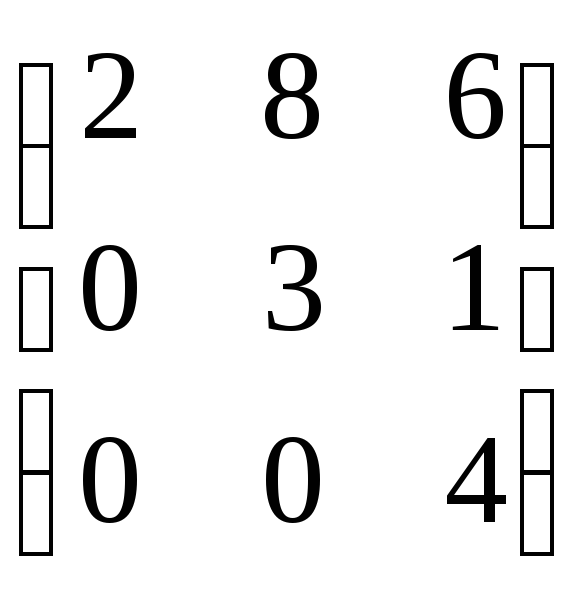
а) 3

б) 2

с) 0

4. Свойства операции транспонирования

а) (А’)’ = A

(A)’ = A’

(A+B)’ = A’ + B’

(AB)’ = B’A’

б) (A^-1)^-1 = A

(AB)^-1 = B^-1A^-1

(A^-1)’ = (A’)^-1

c) AB  BA

AE = EA

A^-1A = AA^-1 = E

5. Свойства обратных матриц

а) (A^-1)^-1 = A

(AB)^-1 = B^-1A^-1

(A^-1)’ = (A’)^-1

б) (А’)’ = A

(A)’ = A’

(A+B)’ = A’ + B’

(AB)’ = B’A’

c) (A^-1)’ = (A’)^-1

(А’)’ = A

(A^-1)^-1 = A

6. Найти сумму матриц А и В, если

;

а)

б)

в)

7. Найти произведение матриц А и В, если

;

а)

б)

в)

8. Найти матрицу А^-1, обратную к матрице

а)

б)

в)

9. Найти определитель матрицы третьего порядка

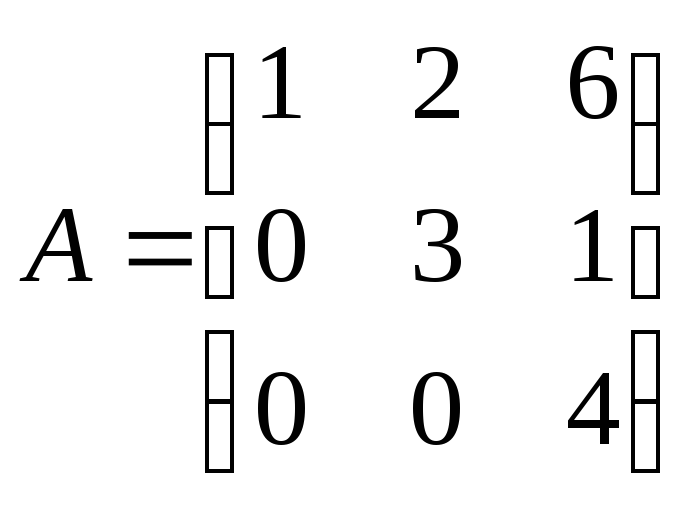
а) 12

б) 0

в) 18

10. Рангом матрицы А называется

а) наивысший порядок отличных от нуля миноров этой матрицы

б) количество строк матрицы А

в) количество столбцов этой матрицы

11. Элементарные преобразования матрицы, не меняющие ранга матрицы:

а) – отбрасывание нулевой строки (столбца)

• умножение всех элементов строки (столбца) матрицы на число , не равное нулю

• изменение порядка строк (столбцов) матрицы

• прибавление к каждому элементу одной строки (столбца) соответствующих элементов другой строки (столбца), умноженных на любое число

• транспонирование матрицы

б) Сложение матриц и умножение матрицы на число

в) - отбрасывание столбца матрицы, состоящего из нулей

• умножение элементов матрицы на любое число

• прибавление к каждому элементу одной строки соответствующих элементов другого столбца

12. Теорема о ранге матрицы:

а) Ранг матрицы равен максимальному числу ее линейно независимых строк или столбцов

б) Ранг матрицы равен количеству всех строк и столбцов матрицы

в) Ранг матрицы равен размеру матрицы

13. Если определитель матрицы системы n линейных уравнений с n переменными  = А  0, то единственное решение системы АХ = В определяется методом обратной матрицы по формуле

а) Х = А^-1В

б) , (j = 1, …, n)

в) Х = АВ^-1

14. Если  = А  0, то решение СЛЦ вида АХ = В определяется по формуле Крамера:

а) , (j = 1, …, n), где _j – определитель матрицы, получаемой из матрицы А заменой j-го столбца столбцом свободных членов В

б) Х = А^-1В

в) Х = А+В

15. Система m линейных уравнений с n неизвестными совместима тогда и только тогда, когда выполняется условие:

а) ранг матрицы системы А равен рангу расширенной матрицы (АВ)

в) А  0

в) m=n

16. Совместная система имеет единственное решение, если

а) r=n

б) r>n

в) r<n

17. Система m линейных уравнений с n неизвестными называется однородной , если все свободные члены равны

а) 0

б) 1

в) –1

18. Если е₁, е₂, …, е_к являются фундаментальной системой решений системы АХ = 0, то общее решение системы имеет вид:

а) с₁е₁ + с₂е₂ + …+ с_ке_к

б) е₁ + е₂ + …+ е_к

в) е₁ * е₂ * … * е_к

19. В уравнениях основной задачи межотраслевого баланса Х = АХ + У

а) Х – вектор валового выпуска

У – вектор конечного продукта

А – матрица прямых затрат

б) (поменяй местами Х и У)

в) (поменяй местами Х и А)

20. В уравнениях, называемых соотношениями межотраслевого баланса, матрицей полных затрат называется матрица:

а) S = (E - A)^-1

б) Х = (E - A)^-1У

в) Х = АУ

21. Система из трех уравнений с тремя переменными, заданная в матричном виде АХ = В, совместна в следующих случаях:

а) r(A) = r(АB) = 3

б) r(A)  r(АB)

в) r(A) = 3

22. Какие из приведенных матриц являются продуктивными:

а)

б)

в)

23. Векторы называются поллинеарными, если выполняется условие:

а) они лежат на одной прямой или параллельных прямых

б) они лежат на перпендикулярных прямых

в) они лежат в одной плоскости

24. Векторы называются компланарными, если они удовлетворяют условию:

а) они лежат в одной плоскости или в параллельных плоскостях

б) они сонаправлены

в) они противоположно направлены

25. Длина вектора (x, y, z) определяется по формуле:

а) =

26. Проекцией вектора на ось l называется число :

а) = cos, где  - угол наклона к оси l

б) =

в) = cos, где  - угол наклона к оси l

27. Скалярным произведением (,) двух векторов и называется число

а) = || * || * cos

б) = || * ||

в) = || * cos

28. Скалярным произведением двух векторов = (x₁, y₁, z₁) и = (x₂, y₂, z₂)

а) = x₁y₁ + y₁y₂ + z₁z₂

б) = x₁y₂ + y₁y₂ + z₁х₂

в) = x₁ + y₁ + z₁

29. Угол  между векторами (1, 0 ,1) и (0, 2, 1) равен

а) cos =

б) cos = 1

в) cos = ½

30. Формула вычисления угла  между векторами = (x₁, y₁, z₁) и = (x₂, y₂, z₂)

а) cos =

б) cos =

в) cos = ||||

31. Определение ортогональности двух векторов

а) = 0

б) =

в) -=0

32. Условие коллиниарности двух векторов и

а)

б) x₁у₁ + х₂y₂ + z₁z₂ = 0

в) =0

33. Условие ортогональности двух векторов = (x₁, y₁, z₁) и = (x₂, y₂, z₂)

а) x₁х₂ + y₁y₂ + z₁z₂ = 0

б)

в) -=0

34. Найти длину вектора = (4, 0, 3)

а) 5

б) 7

в) 12

35. Разложите вектор = (3, 4, 5) по векторам = (1, 0 , 0), = (0, 1 , 0), = (0, 0, 1)

а) =3+4+5

б) =++

в) =2+3+4

36. Найти координаты вектора , если = +2, = (1, 4, 0), = (0, 1, 2)

а) (1, 6, 4)

б) (1, 5 ,2)

в) (1, 3, -2)

37. Вектор называется линейной комбинацией векторов ₁, ₂, …, _m, если выполняется условие:

а) =₁₁ + ₂₂+…+_mm

б) (₁+₂+…+_m)=0

в) векторы лежат в одной плоскости

38. Вектор 0 называется собственным вектором линейного оператора А, если выполняются условия:

а) А = ,  - некоторое число

б) А = 0

в) А() = А

39. Характеристическим уравнением оператора А называется уравнение

а) |А-Е| = 0

б) |А-Е| = 1

в) А=

40. Какие из приведенных троек векторов образуют базис в пространстве R³

а) (1, 0, 0), (0, 1, 0), (0, 0, 1)

б) (1, 1, 0), (1, 0, 1), (0, 1, 1)

в) (1, 1, 1), (1, 0 , 0), (1, 0, 1)

41. Расстояние d между двумя точками М₁(х₁, у₁) и М₂(х₂, у₂) находится по формуле

а)

б) d = x₁x₂ + y₁y₂

в) d = x₁y₁ + x₂y₂

42. Координаты (х, у) точки М – середины отрезка с концами А(5, 6) и В(3, 8)

а) (4, 7)

б) (8, 14)

в) (2, -2)

43. Координаты (х,у) точки М, делящей отрезок М₁(х₁, у₁) и М₂(х₂, у₂) в отношении , находятся по формуле:

а) ,

б) х = х₁ + (1-)х₂

у = у₁ + (1-)у₂

в) х = х₁ + х₂

у = у₁ + у₂

44. Уравнение прямой с угловым коэффициентом k и начальной ординатой b:

а) у = kx+b

б) y = k+x

в) y = bx+k

45. Найти общее уравнение прямой:

а) Ах+Ву+С=0

б)

в)

46. Найти общее уравнение плоскости:

а) Ах+Ву+Сz+D=0

б)

в) Ах+Ву+Сz =1

47. Найти расстояние d от точки А(0, 1) до прямой 4х+3у+2=0

а) 1

б) 7

в) 5

48. Угол между у=k₁x+b₁ и у = k₂x+b₂ находится по формуле:

а)

б)

в)

49. Условие параллельности прямых у =k₁x+b₁, у = k₂x+b₂

а) k₁ = k₂

б) k₁k₂ = -1

в) k₁k₂ = 1

50. Условие перпендикулярности прямых

а) k₁k₂ = -1

б) k₁ = k₂

в) k₁k₂ = 1

51. Общее уравнение кривых второго порядка:

а) Ах²+Вху+Су²+Еу+F=0

б) (х-х₀)²+(у-у₀)²=R²

в)

52. Общее уравнение окружности с центром в точке О(а, b) и радиусом R

а) (х-а)²+(у-b)²=R²

б)

в)

53. Каноническое уравнение эллипса

а)

б)

в) (х-а)²+(у-b)²=1

54. Каноническое уравнение гиперболы

а)

б) (х-а)²+(у-b)²=1

в)

55. Каноническое уравнение параболы

а) у²=2рх

б) у²=2х

в) у²=х+у

56. Эксцентриситет эллипса

а) =с/а

б) =a/b

в) =с/аb

57. Составить уравнение окружности с центром в точке А(1,2) и радиусом 10:

а) (х-1)²+(у-2)²=100

б) (х+1)²+(у+2)²=10

в) (х-1)²+(у-2)²=10

58. Найти центр и радиус окружности (х+1)²+у²=225

а) А(-1,0), R=15

б) А(1,0), R=25

в) А(0,1), R=15

59. Уравнение плоскости, отсекающей на трех координатных осях отрезки, равные 2, 3, 4

а) х/2 + у/3 + z/4 = 1

б) 2х + 3у + 4z = 1

в) 2(х-2) + 3(х-3) + 4(х-4) = 0

60. Уравнение плоскости, перпендикулярной вектору =(5, 2, 4) и проходящей через точку М(3, 2 ,1)

а) 5(х-3) + 2(х-2) +4(х-1) = 0

б) х-3 = (у-2)/2 = (z-1)/4

в) 3х + 2у + z = 10

61. Уравнение прямой в пространстве, проходящей через точку М(3, 2 , 1) с направляющим вектором =(5, 2 , 4)

а)

б) 3х + 2у + z = 11

в)

62. Уравнение прямой , проходящей через две заданные точки М₁(1, 2 , 3) и М₂(4, 5 , 6)

а)

б)

в) 4х + 6у + 8z = 6

63. Угол  между двумя прямыми с направляющими векторами ₁=(m_­1, n₁, p₁), ₂=(m_­2, n₂, p₂)

а) cos = 

б) tg = m₁m₂ + n₁n₂ + p₁p₂

в) sin = m₁ + п + р

64. Условие параллельности двух прямых в пространстве с направляющими векторами ₁=(m_­1, n₁, p₁), ₂=(m_­2, n₂, p₂)

а)

б) m₁m₂ + n₁n₂ + p₁p₂ = 0

в) m₁ = m₂, n₁ = n₂, p₁ = p₂

65. Условие перпендикулярности двух прямых в пространстве с направляющими векторами ₁=(m_­1, n₁, p₁), ₂=(m_­2, n₂, p₂)

а) m₁m₂ + n₁n₂ + p₁p₂ = 0

б) m₁ + m₂ + p₁ = n₁ + n₂ + p₂

в)

66. Условие параллельности прямой и плоскости

а) А_m + B_n + C_p = 0

б)

в) А_m + B_n + C_p = 1

67. Условие перпендикулярности прямой с направляющим вектором =(m_­, n, p) и плоскости А_x + B_y + C_z = 0

а)

б) А_m + B_n + C_p = 0

в) А_m + B_n + C_p = 1

68. Являются ли прямые 2х – у + 3 = 0 и 4х + 8у + 17 = 0 перпендикулярными

а) да

б) параллельны

в) пересекаются под острым углом

69. Найти координаты центра (х₀, у₀) и радиуса R окружности (х+1)² + (у-2)² = 121

а) (-1,2), R = 11

б) (1,2), R = 121

в) (2,1), R = 11

70. Найти расстояние между фокусами эллипса

а) 8

б) 16

в) 64

71. Найти расстояние между фокусами гиперболы

а) 20

б) 100

в) 10

72. Составить уравнение плоскости, проходящей через точку М₀(2, 3 ,-1) параллельно плоскости 4х – 2у + 5z – 3 = 0

а) 4х – 2у + 5z + 3 = 0

б) 4х – 2у + 5z + 6 = 0

в) 2х – 3у + z – 3 = 0

73. Найти область определения функции

а) x>0

б) x0

в) x<0

74. Определение нечеткой функции у = f(x)

а) f(-x) = -f(x)

б) f(-x) = f(x)

в) f(x+t) = f(x)

75. Какие из функций являются сложными 1) y = arcsinx 2) y = arcsin3x 3) y = 5tgx

а) 2

б) 3

в) 1

76. Какая функция называется бесконечно большой величиной при х х₀

а)

б)

в)

77. Какая функция называется бесконечно малой величиной при х х₀

а)

б)

в)

78. Что называется первым замечательным пределом

а)

б)

в)

79. Что называется вторым замечательным пределом

а)

б)

в)

80. Найти предел

а) 1

б) 0

в)

81. Найти предел с помощью правила Лопиталя

а) 0

б) 1

в)

82. Какие из функций бесконечно малые при х0, у = х¹⁰, у = cosх, у = х²+1

а) у = х¹⁰

б) у = cosх

в) у = х²+1

г) никогда

83. Какие из функций бесконечно большие при х, у = arctgx, y=x², y=1/x

а) y=x²

б) y=1/x

в) у = arctgx

г) никогда

84. Какой величиной является произведение двух бесконечно малых величин

а) бесконечно малая

б) бесконечно большая

в) неопределенностью

г) число 2

85. Какой величиной является произведение двух бесконечно больших величин

а) бесконечно большая

б) бесконечно малая

в) неопределенность

г) некоторое конечное число

86. Какая из функций является непрерывной всюду

а) y = sinx

б) у = 1/х

в) у = tgх

г) у = ctgх

87. Найти производную функции

а)

б)

в) –3

88. Найти верное правило дифференцирования

а) (uv)’ = u’v + uv’

б) (uv)’ = u’v – uv’

в) (uv)’ = u’v’

89. Найти вторую производную функции у=sinx

а) -sinx

б) cosx

в) sinxcosx

90. Найти верное уравнение касательной k кривой y=f(x) в точке х₀

а) y – f(x₀) = f’(x₀)(x-x_o)

б) y = f(x₀)(x-x₀)

в) y-f’(x₀) = f(x₀)(x-x₀)

91. Найти точку перегиба функции у = 5х³-3х²+1

а) 1/5

б) 0

в) 4

92. Найти вертикальную асимптоту функции

а) х=2

б) х=-2

в) у=2

г) х=0

93. Укажите горизонтальные асимптоты функции у = arctgx

а) у=/2, у=-/2

б) х=/2, х=-/2

в) х=0

г) у=0

94. Найти точки пересечения графика функции у=3х-х³ с осью (ох)

а) 0;

б) 0

в) 3

г) –3

95. Найти точки экстремума функции у=3х-х³

а) х=1; х=-1

б) х=0

в) х=3; х=-3

96. Найти вертикальную асимптоту графика функции

а) х=

б) у =

в) х = 4

97. Найти горизонтальную асимптоту графика функции

а) у =

б) х=

в) 2х+4

98. Найти точки перегиба графика функции у = х³ – 6х² + 12х +4

а) х=2

б) х=3

в) х=0

99. Найти производные функции у = 4х⁵ – 2х³ + 3

а) 20х⁴ – 6х²

б) 20х – 2

в) 4х⁴ – 2х²

100. Найти уравнение касательной k кривой в точке х=2