Рис. 2

V. Изучение нового материала, его восприятие и осмысление

1. Понятие равномерного движения по окружности.

Линейная и угловая скорость При прямолинейном движении траектория движения — прямая линия, а направление вектора скорости всегда совпадает с направлением перемещения. Что можно сказать о направлении перемещения и скорости при криволинейном движении? Какие еще характеристики его описывают?

В школьном курсе мы изучаем простейший вид криволинейного движения — равномерное движение по окружности.

Равномерное движение материальной точки по окружности —

это движение, при котором тело за любые равные промежутки времени совершает одинаковые перемещения, то есть проходит дуги равной длины.

Например, тело движется из точки А в точку В по криволинейной траектории (рис. 3). При этом пройденный путь — это длина дуги АВ, а модуль перемещения — это длина хорды АВ (собственно перемещение направлено вдоль этой хорды).

Рис. 3

Вектор скорости движения тела направлен вдоль хорды, то есть вдоль вектора перемещения. Если сделать линейные участки более короткими, то вектор скорости на каждом из них все равно будет направлен вдоль хорды. Продолжая уменьшать длину прямолинейных участков, мы приближаем ломаную линию к плавной кривой. Вектор скорости на каждом из них по-прежнему направлен вдоль хорды по касательной к кривой в данной точке (рис.4). Эту скорость называют линейной (или мгновенной) скоростью.

Рис. 4

Линейная, или мгновенная, скорость — это скорость, с которой тело движется по окружности.

Модуль линейной скорости можно определить отношением длины дуги ко времени, за которое эта дуга пройдена.

Линейная скорость в каждой точке криволинейной траектории направлена по касательной к траектории. В этом несложно убедиться, рассмотрев демонстрации.

Демонстрация 1 (слайд-шоу, рисунки, фото и т. п.).

Работа на точиле (рис. 5): раскаленные частички, отрываясь, летят по касательной к окружности, по которой деталь прикасается к точильному кругу.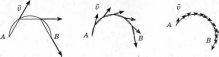

Рис. 6

Вопросы классу

Рис. 7

Рис. 5

Буксование колеса автомобиля (рис. 6): мел­кие частички земли, камушки, брызги воды движутся по касательной.

Фейерверк-шоу (рис. 7): раскаленные частич­ки отрываются и движутся по касательной к окружности. Эта демонстрация может быть показана и в реальных условиях с помощью бенгальского огня.

Что общего и чем отличаются линейная скорость при движении по прямой и по окружности? (Модуль линейной скорости вычисляется как отношение модуля перемещения ко времени для обоих видов движения, но, в отличие от прямолинейного движения, где вектор скорости остается неизменным в течение всего движения, при движении по окружности вектор линейной скорости все время меняет свое направление, при этом оставаясь перпендикулярным к радиусу окружности.)

Движение по окружности характеризуется также и с помощью угловой скорости.

Угловая скорость равномерного движения по окружности — это скорость, модуль которой равен отношению угла поворота радиуса, соединяющего материальную точку с центром окружности, ко времени этого поворота (рис. 8).

Угловая скорость обозначается символом со; измеряется в СИ в радианах в секунду (рад/с). р_ИС- 8

1. рад/с — это угловая скорость, при которой за каждую секунду радиус, соединяющий материальную точку с центром окружности, поворачивается на угол 1 радйан:

Ф

1. = — , где ф — угол поворота радиуса. t

iiil 2. Период и частота вращения

Равномерное движение по окружности является движением периодическим, то есть таким, при котором положение тела через равные интервалы времени повторяются. Как периодическое движение оно характеризуется периодом и частотой вращения.

Период вращения — это отношение времени движения к числу вращений, сделанных за это время:

Физический смысл периода вращения: период — это время, за которое тело совершает один полный оборот. При равномерном движении по окружности период является постоянной величиной. •

Период — величина скалярная, в СИ измеряется в секундах (с). Частота вращения — это отношение числа вращений ко време-

N

ни, за которое они осуществлены: v = —.

t

Физический смысл частоты вращения: частота вращения равна числу вращений за единицу времени.

Частота — скалярная величина, в СИ измеряется в 1/с (с^-1). Демонстрация 2. Вращение диска проигрывателя или лопастей вентилятора с разной частотой.

Задания классу

1. Приведите примеры устройств, где используется вращение частей с разной частотой.

2. К какому результату это приводит в каждом из приведенных примеров?

Учитель комментирует формулы, связывающие некоторые величины, описывающие движение по окружности; учащимся уместно записать их в тетради.

Величины, которые связывает формула	Формулы у
Период и частота
Угловая скорость и период
Угловая скорость и частота	С0 = 2rtV
Линейная скорость, период и радиус окружности
Линейная скорость, частота и радиус окружности	v = 2nRv
Линейная скорость, угловая скорость и радиус окружности	v = (i»R

3. Центростремительное ускорение

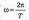
Еще одна из важных характеристик равномерного движения по окружности — центростремительное ускорение.

Задание классу

Ознакомьтесь с текстом учебника и самостоятельно составьте характеристику центростремительного ускорения как физической величины по обобщенному плану характеристики физической величины (см. прил. 14).

Центростремительное ускорение как физическая величина

1. Центростремительное ускорение характеризует скорость изменения линейной скорости по направлению.

2. Центростремительное ускорение — это векторная физическая величина, которая в каждой точке окружности направле- ' на вдоль радиуса к центру окружности и численно равна отношению квадрата линейной скорости и радиуса окружности (рис. 9).

Для равномерного движения по окружности модуль центростремительного ускорения — постоянная величина.

3. 

4. 

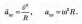
5. Определяется путем косвенных измерений.

Решение задач (устно)

1. Вентилятор совершает один оборот за 0,5 с. С какой частотой он вращается? (2 с^-1.)

2. Частота вращения компакт-диска в CD-приводе 100 с"¹. Определить период вращения диска. (0,01 с.)

3. С какой линейной скоростью двигалось равномерно тело по окружности радиусом 50 м, если за 10 мин оно произвело 60 оборотов?

   

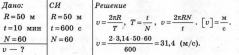
   Ответ: и = 31,4 м/с.

   Решение задач (письменно)

   (Решение задачи комментирует учитель.)

   Минутная стрелка в два раза длиннее часовой. Определите отношение центростремительных ускорений концов этих стрелок.

   

Домашнее задание

1. Выучить теоретический материал по учебнику.

2. Решить задачи.

1. Кулер микропроцессора компьютера вращается с частотой 3000 об/мин. С каким периодом кулер вращается?

2. Линейная скорость точек рабочей поверхности шлифовального круга диаметром 300 мм не должна превышать 35 м/с. Можно ли его насадить на вал, вращающийся с частотой 1400 об/мин?

3. Секундная стрелка в 2 раза короче часовой. У какой из этих стрелок линейная скорость движения конца стрелки больше? Во сколько раз?