Физика
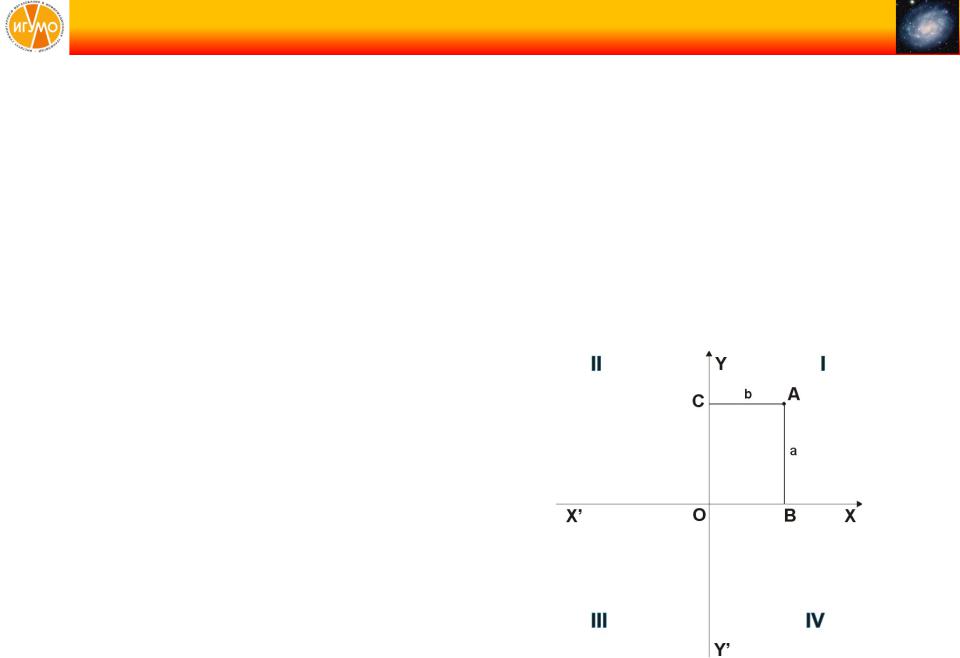
Ординатой (от лат. ordinatus — расположенный в порядке) точки A называется координата этой точки на оси y в прямоугольной системе координат. Величина ординаты точки A равна длине отрезка OC (см. рис. 1). Если точка C принадлежит положительной полуоси OY, то ордината имеет положительное значение. Если точка C принадлежит отрицательной полуоси Y’O, то ордината имеет отрицательное значение. Если точка A лежит на оси X’X, то её ордината равна нулю.
В прямоугольной системе координат ось |
«осью |
ординат». |
|
Система отсчёта
OX — ось абсцисс, OY — ось ординат, OZ — ось аппликат.
Физика
Абсциссой (лат. abscissa — отрезок) точки A называется координата этой точки на оси X’X в прямоугольной системе координат. Величина абсциссы точки A равна длине отрезка OB (см. рисунок). Если точка B принадлежит положительной полуоси OX, то абсцисса имеет положительное значение. Если точка B принадлежит отрицательной полуоси X’O, то абсцисса имеет отрицательное значение. Если точка A лежит на оси Y’Y, то её абсцисса равна нулю.
В прямоугольной системе координат луч
называется «осью абсцисс». При функций, ось абсцисс обычно используется как функции.
Система отсчёта
OX — ось абсцисс, OY — ось ординат, OZ — ось аппликат.
Физика
Аппликатой точки A называется координата этой точки на оси OZ в прямоугольной трёхмерной системе координат. Величина аппликаты точки A равна длине отрезка OD. Если точка D принадлежит положительной полуоси OZ, то аппликата имеет положительное значение. Если точка D принадлежит отрицательной полуоси OZ, то аппликата имеет отрицательное значение. Если точка A лежит на плоскости XOY, то её аппликата равна нулю.
Слово «аппликата» происходит от лат. applicata, что означает «приложенная». Имеется в виду, что координата Z (аппликата) была приложена к уже имевшимся двум координатам на плоскости: абсциссе и ординате.
В прямоугольной системе координат ось OZ называется «осью
аппликат».
Обычно понятие аппликата встречается в теории
комплексного переменного, где тригонометрические
Система отсчёта
теряют периодичность. Поэтому вводится новая ось,
OX — ось абсцисс, OY — ось ординат, OZ — ось аппликат
аппликатой по которой откладывается модуль
числа
Физика
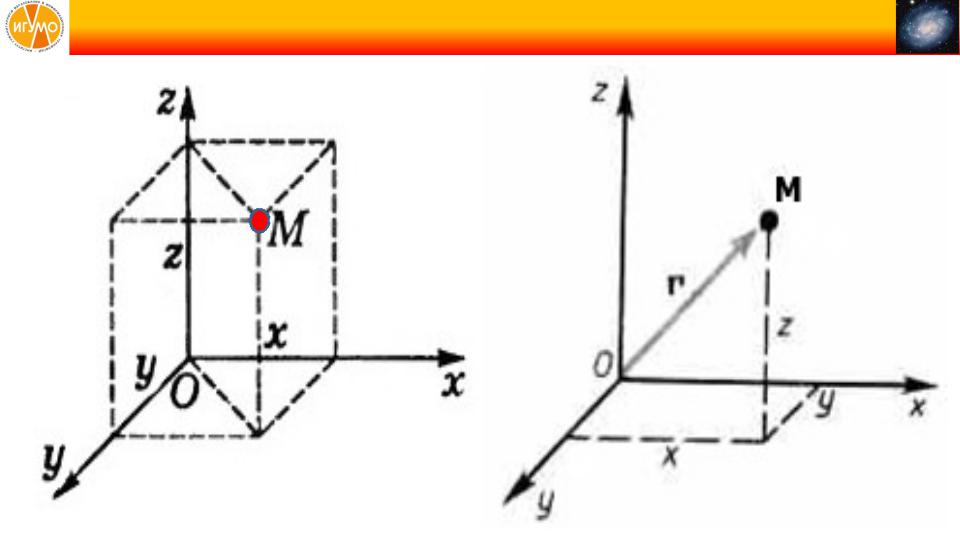
Точка и её
Возьмем какую-нибудь точку |
Проведем из начала координат |
в пространстве, М (x, y, z). |
к точке М вектор . |
Здесь x, y, z – координаты |
Этот вектор называется |
точки М в данной системе |
радиус–вектором точки М. |
координат. |
|
Физика
Единичным вектором или ортом называется вектор, длина которого равна единице и который направлен вдоль какой- либо координатной оси. i
Единичный вектор, направленный вдоль оси x, обозначаетсяj .
Единичный вектор, направленный вдоль оси y, обозначается |
|
. |
k |
i j k |
|
Единичный вектор, направленный вдоль оси z, обозначается
.
Вектора , , называются координатными векторами.
r x i y j z k
Радиус-вектор точки М можно представить на соответствующие
М:
Орты и радиус-вектор точки
Физика
Траектория движения
Движение любой материальной точки можно показать с помощью прямой или кривой линии.
Траектория — это непрерывная линия, которую описывает материальная точка относительно выбранной системы отсчета. Задание - приведите примеры:
а) траектории тел; б) видимых и невидимых траекторий тел (траектория
колес велосипеда на мокром песке и мела на доске во время письма видимая; траектория полета пчелы и движения колес автомобиля по асфальту невидимая); в) траекторий, известных еще до начала движения (траектория движения рейсового трамвая, искусственного спутника Земли).
В зависимости от траектории механическое движение можно разделить на два вида:
Траектория движения
Физика
Траектория движения
На практике форму траектории задают с помощью математических формул
(y = f(x) — уравнение траектории)
или изображают на рисунке.
Вид траектории зависит от выбора системы отсчета.
Например, траекторией тела, свободно падающего в вагоне, который движется равномерно и прямолинейно, является прямая вертикальная линия в системе отсчета, связанной с вагоном, и парабола в системе отсчета, связанной с Землей.
Физика
5.Траектория движения
Взависимости от вида траектории различают
прямолинейное и криволинейное движение.
Взависимости от скорости различают равномерное (скорость не изменяется) и неравномерное
(ускоренное, равноускоренное, прерывистое) движение
Физика
Путь
По траектории легко установить путь, пройденный материальной точкой за какой-либо промежуток времени.
Путь — это длина траектории, которую описывает материальная точка за данный промежуток времени.
Путь обозначают символом l. Единица в СИ — метр (м). Путь — скалярная величина.
Он увеличивается, если тело движется, и остается неизменным, если тело находится в покое, т. е. путь не может уменьшаться со временем.
Путь l — скалярная физическая величина, определяемая длиной траектории, описанной телом
за некоторый промежуток времени. Путь всегда