26. Формула повної ймовірності

Формула повної ймовірності дозволяє обчислити ймовірність деякої події через умовні ймовірності цієї події в припущенні якихось гіпотез, а також ймовірностей цих гіпотез.

Нехай дано імовірнісний простір, іповна група подій, таких що. Хайподія, що цікавить нас. Тоді

.

Зауваження 

Формула повної ймовірності також має наступну інтерпретацію. Нехай -випадкова величина, що маєрозподіл.

Тоді,

тобто апріорна ймовірність події рівна середньомуйого апостеріорної ймовірності.

27. Формула Баєса

Формула Баєса:

де — апріорна ймовірність гіпотези A;

—ймовірність гіпотези A при настанні події B (апостеріорна ймовірність); — ймовірність настання події B при істинності гіпотези A;

—ймовірність настання події B.

Формула виводиться із визначення умовної ймовірності: Наслідок

Важливим наслідком формули Баєса є формула повної ймовірності події, що залежить від декількох несуміснних гіпотез (і тільки від них).

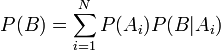—ймовірність настання події B, що залежить від гіпотез , якщо відомі їх ступені достовірності.

28. Повторні незалежні випробування

Повторні незалежні випробування називають схемою Бернуллі, якщо при кожному випробуванні можливі лише два наслідки: подія А (успіх) або  Ā (невдача)­ і ймовірність  появи  події  А  при  кожному  випробуванні  дорівнює  р ( 0 < р < 1).    Якщо проводиться серія випробувань, в результаті якої може відбутись подія А з певною ймовірністю. Якщо ймовірність події А в кожному випробуванні не залежить від результатів інших випробувань, то такі випробування називаються незалежними відносно події А.

формула Бернуллі

У теорії ймовірності, формула Бернуллі дозволяє обчислити ймовірність успіхів у серії незалежних експериментів.

Якщо ймовірність настання подіїв кожному з випробувань стала, то ймовірністьтого, що подіянастанеразів внезалежних випробуваннях дорівнює :

або Зауваження

1. Ймовірність появи події А у випробувальні схеми Бернуллі менше ніж 5 р. знаходиться:

P_n ( k<m) = P_n(0) + P_n ( 1) +……+ P_n ( m-1),

а ймовірність появи подія А в кількості випробувань не менше за m обчислюється:

P_n ( k>=m)= P_n(m)+ P_n(m+1)+….. P_n(n)

P_n ( k>=m)= 1- P_n(k).

2. У багатьох випадках потрібно знаходити найбільш ймовірне значення числа появи А:

np- q<=m₀<= np+p

(n+1)(p-1) <=m₀<=(n+1)p

Значення числа m₀ повинно бути цілим.

3. Якщо ймовірність появи події А у кожному випробуванні дорівнює р, тоді кількість випробувань, які потрібно здійснити, щоб з ймовірністю р стверджувати, що подія А відбувається хоча б в одному випробуванні, обчислюється:

n >

29.Випадкові величини

• Випадкова величина - це величина, яка в результаті випробувань може приймати певні значення (із сукупності своїх значень) з певною ймовірністю. Випадковою можна назвати будь-яку (не обов'язково чисельну) змінну x, значення якої х створюють множину випадкових елементарних подій {х}.

• Розрізняють дискретну і неперервну випадкові величини.

• Дискретною випадковою величиною називається випадкова величина, що приймає скінчене число значень з множини, елементи якої можна пронумерувати.

• Неперервною випадковою величиною називається випадкова величина, можливі значення якої неперервно заповнюють деякий інтервал.

• Рядок розподілу дискретної випадкової величини x може бути представлений як у табличній формі - у вигляді таблиці, де перераховано значення випадкової величини х1, х2, хп з відповідними до них ймовірностямир1, р2, рп , так і у вигляді графічного зображення.

30.Основні завдання та методи математичної статистики

Математична статистика - це сучасна галузь математичної науки, яка займається статистичним описом результатів експериментів і спостережень, а також побудовоюматематичних моделей, що містять поняття ймовірності.Теоретичною базою математичної статистики служить теорія ймовірностей.

В структурі математичної статистики традиційно виділяють два основні розділи: описова статистика і статистичні висновки .

Описова статистика використовується для:

o узагальнення показників однієї змінної (статистика випадкової вибірки);

o виявлення взаємозв'язків між двома і більше змінними (кореляційно-регресійний аналіз).

Описова статистика дає можливість отримати нову інформацію, швидше зрозуміти і всебічно оцінити її, тобто виконує наукову функцію опису об'єктів дослідження, чим і виправдовує свою назву. Методи описової статистики покликані перетворити сукупність окремих емпіричних даних на систему наочних для сприйняття форм і чисел: розподіли частот; показники тенденцій, варіативності, зв'язку. Цими методами розраховуються статистики випадкової вибірки, які служать підставою для здійснення статистичних висновків.