
- •Основні методі знаходження невизначеного інтегралу. Метод безпосереднього інтегрування
- •Метод інтегрування частинами
- •3. Інтегрування раціональних ф-ій
- •9.Застосування визначеного інтеграла до знаходження площі фігури та об’єму тіла обертання
- •12. Диференціальні рівняння зі сталими коефіцієнтами. Теореми про структуру розвязків о.Л. Д.Р і н.Л.Д.Р.
- •14. Ознаки збіжності додатніх рядів
- •15. Знакозмінні ряди. Абсолютна та умовна збіжність. Теорема Лейбніца
- •17. Застосування степеневих рядів
- •18. Поняття про випадкові події. Простір елементарних подій
- •19.Класифікація подій:
- •20. Класичне означення ймовірності і її властивості.
- •22) Означення ймовірності та її властивості
- •23. Основні формули комбінаторики
- •24. Теорема додавання ймовірностей.
- •25.Теорема множення ймовірностей.
- •26. Формула повної ймовірності
- •27. Формула Баєса
- •28. Повторні незалежні випробування
- •29.Випадкові величини
17. Застосування степеневих рядів
обчислення значень функцій
Нехай
потрібно обчислити значення функції
f(x) при х = х1 із заданою точністю
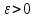
Якщо
функцію f(x) в інтервалі (-R; R) можна
розкласти у степеневий ряд f(x) =
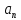 +
+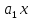 +
+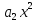 +… +
+… +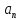
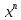 + … і
+ … і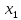
 (-R; R), то точне значення f(x1) дорівнює сумі
ряду при х = х1, тобто f(x) =
(-R; R), то точне значення f(x1) дорівнює сумі
ряду при х = х1, тобто f(x) =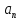 +
+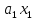 +
+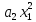 + … +
+ … +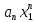 + …., а наближене - частковій сумі
+ …., а наближене - частковій сумі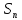 (
(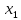 )
тобто f(x)
)
тобто f(x)
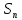 (
(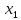 )
=
)
=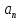 -
- -
- + …+
+ …+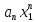 .
.
Точність цієї рівності збільшується із зростанням n.
обчислення визначених інтегралів
Степеневі
ряди застосовуються також для наближеного
обчислення невизначених і визначених
інтегралів у випадках, коли первісна
не виражається в кінцевому вигляді
через елементарні функції або знаходження
первісної складне. Нехай треба обчислити
з точністю до
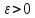 Якщо підінтегральну функцію можна
розкласти у ряд за степенями х і інтервал
збіжності (-R, R) містить відрізок
інтегрування, то для обчислення заданого
інтеграла можна скористатися властивістю
почленного інтегрування цього ряду.
Помилку обчислень визначають так само,
як і при обчисленні значень функцій.
Якщо підінтегральну функцію можна
розкласти у ряд за степенями х і інтервал
збіжності (-R, R) містить відрізок
інтегрування, то для обчислення заданого
інтеграла можна скористатися властивістю
почленного інтегрування цього ряду.
Помилку обчислень визначають так само,
як і при обчисленні значень функцій.
розв’язання диференціальних рівнянь
Якщо розв’язок диференціального рівняння не виражається через елементарні функції в кінцевому вигляді або спосіб його розв’язання складний, то для наближеного розв’язання рівняння можна скористатися рядом Тейлора. Спосіб послідовного диференціювання застосовується для розв’язанняння диференціальних рівнянь будь-якого порядку.
18. Поняття про випадкові події. Простір елементарних подій
Випадкова
подія — подія, яка при заданих умовах
може як відбутись, так і не відбутись,
при чому існує визначена ймовірність
p (0 ≤ p ≤ 1) того, що вона відбудеться при
заданих умовах. Випадкова подія є
підмножиною простору елементарних
подій. Те, що випадкова подія має деяку
ймовірність проявляється в поведінці
її частоти: якщо вказані умови повторити
N
раз, то
подія А
выдбудеться при цьому
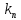 (A)
раз, то частота
(A)
раз, то частота
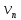 (A)
=
(A)
=
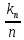 реалізації подіїA
при великих N
стає
близькою до P.
Подія може вважатися випадковою лише
коли вона може повторитись довільну
кількість разів. Кожному випадковому
експерименту ставлять у відповідність
множину елементарних подій, яка зветься
простором елементарних подій і
позначається W або Ω, також S. Кожна подія
ототожнюється з деякою підмножиною
простору елементарних подій. Зокрема,
вірогідній події відповідає весь простір
елементарних подій, неможливій події
? - пуста підмножина. Підмножини й події,
що їм відповідають, позначаються однією
і тією ж літерою. Якщо кожна з елементарних
подій w1,w2, w3, … така, що
реалізації подіїA
при великих N
стає
близькою до P.
Подія може вважатися випадковою лише
коли вона може повторитись довільну
кількість разів. Кожному випадковому
експерименту ставлять у відповідність
множину елементарних подій, яка зветься
простором елементарних подій і
позначається W або Ω, також S. Кожна подія
ототожнюється з деякою підмножиною
простору елементарних подій. Зокрема,
вірогідній події відповідає весь простір
елементарних подій, неможливій події
? - пуста підмножина. Підмножини й події,
що їм відповідають, позначаються однією
і тією ж літерою. Якщо кожна з елементарних
подій w1,w2, w3, … така, що
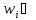 А, (і = 1,2, …) і нема інших елементарних
подій з такою властивістю, пишуть А =
{w1,w2,w3, ...}. Вибір форми зображення простору
елементарних подій залежить від контексту
й міркувань зручності. Таким чином, для
опису випадкових подій: наслідків
експерименту - застосовують такі точні
поняття: елементарні та складені
випадкові події, простір елементарних
подій. Подія, що може відбутися внаслідок
проведення однієї і лише однієї спроби
(експерименту), називається елементарною
випадковою подією. Елементарні випадкові
події
А, (і = 1,2, …) і нема інших елементарних
подій з такою властивістю, пишуть А =
{w1,w2,w3, ...}. Вибір форми зображення простору
елементарних подій залежить від контексту
й міркувань зручності. Таким чином, для
опису випадкових подій: наслідків
експерименту - застосовують такі точні
поняття: елементарні та складені
випадкові події, простір елементарних
подій. Подія, що може відбутися внаслідок
проведення однієї і лише однієї спроби
(експерименту), називається елементарною
випадковою подією. Елементарні випадкові
події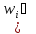 А), які належать відповідно складеним
випадковим подіям А, В, С, тобто є
елементами цих множин, називають
елементарними подіями, які сприяють
появі кожної із зазначених подій
унаслідок проведення експерименту
(тобто сприяють появі події А. Кожному
експерименту (спробі) з випадковими
результатами (наслідками) відповідає
певна множинаW,
елементарних подій {w1,
w2,
w3,
..., wі,…}
(простір елементарних подій), кожна з
яких може відбутися (настати) унаслідок
його проведення.
А), які належать відповідно складеним
випадковим подіям А, В, С, тобто є
елементами цих множин, називають
елементарними подіями, які сприяють
появі кожної із зазначених подій
унаслідок проведення експерименту
(тобто сприяють появі події А. Кожному
експерименту (спробі) з випадковими
результатами (наслідками) відповідає
певна множинаW,
елементарних подій {w1,
w2,
w3,
..., wі,…}
(простір елементарних подій), кожна з
яких може відбутися (настати) унаслідок
його проведення.
