Лабораторна робота № 6

Тема: Методи аналізу часових рядів

Мета: Придбати навички прогнозування значень часового ряду, зокрема, виділення тренда та обліку сезонної складової, а також навички використання засобів Пакет Аналізу та Пошук рішення, що входять в MS Excel.

Порядок виконання роботи:

1) Прогнозування значень часового ряду. Для кожного завдання необхідно:

1. Вивчити теорію.

2. Побудувати графік значень часового ряду.

3. Побудувати графіки прогнозованих значень (для кожного з отриманих прогнозів).

4. Обчислити САО або СООП

5. Відповісти на питання задачі.

2) Складання звіту по лабораторній роботі, в якому представляється:

• формулювання індивідуального завдання;

• відповіді на питання задачі;

• при необхідності, знімки екрану монітора, що містять основні моменти виконання завдання;

• графіки значень часового ряду і прогнозу.

Теорія

Часовим рядом називається послідовність значень деякого показника у часі (наприклад, обсягів продажів, як на рис. 1).

Рис. 1

Аналіз часових рядів є способом виявлення тенденцій минулого та продовження їх в майбутнє. Методи аналізу часових рядів здійснюють прогноз шляхом екстраполяції значень окремої змінної на основі статистичних даних за минулий часовий період. Основне припущення, яке при цьому робиться, полягає в тому - що сталося в минулому дає хороше наближення в оцінці майбутнього.

Розвиток процесів, реально спостережуваних в життя, складається з деякої стійкої тенденції (тренду) і деякої випадкової складової, що виражається в коливанні значень показника навколо тренда. На рис. 2 показано, як можуть залежати обсяги продажів одного і того ж товару на двох стадіях його життєвого циклу (на початку і в кінці продажів).

 

Рис. 2

Криві тренду згладжують часовий ряд значень показника, виділяючи загальну тенденцію. Саме вибір кривої тренду багато в чому визначає результати прогнозування.

У більшості випадків часовий ряд, крім тренда і випадкових відхилень від нього, характеризується ще сезонною складовою. Сезонна складова - це періодичні зміни показника. Звичайна тривалість сезонної складової вимірюється днями, тижнями або місяцями.

Спочатку розглянемо кілька найпростіших методів прогнозування, що не враховують наявності сезонності в часовому ряді. Припустимо, що в журналі Wall Street Journal приведена зведення за останні 12 днів (включаючи сьогоднішній) цін на апельсини, що склалися на момент закриття біржі. Використовуючи ці дані, потрібно передбачити завтрашню ціну на какао (також на момент закриття біржі). Розглянемо кілька способів зробити це.

1. Якщо останнє (сьогоднішнє) значення найбільш значимо в порівнянні з іншими, то воно є найкращим прогнозом на завтра.

2. Можливо, через швидкі зміни цін на біржі перші шість значень вже застаріли і не актуальні, в той час як останні шість значимі і мають рівну цінність для прогнозу. Тоді в якості прогнозу на завтра можна взяти середнє останніх шести значень.

3. Якщо всі значення істотні, але сьогоднішнє 12-е значення найбільш значимо, а попередні 11-е, 10-е, 9-е і т.д. мають все меншу і меншу значимість, слід знайти зважене середнє всіх 12 значень. Причому вагові коефіцієнти для останніх значень повинні бути більше, ніж для попередніх, і сума всіх вагових коефіцієнтів має дорівнювати 1.

Перший спосіб називається «наївним» прогнозом і досить очевидним. Розглянемо докладніше інші способи.

Метод ковзного середнього. Одним з припущень, що лежать в основі даного методу, є те, що більш точний прогноз на майбутнє можна отримати, якщо використовувалися недавні спостереження, причому, чим «новіші» дані, тим їх вага для прогнозу має бути більшою. Дивно, але такий «наївний» підхід виявляється надзвичайно корисним для практики. Наприклад, багато авіакомпаній використовують ковзний тип змінного середнього для створення прогнозів попиту на авіаперельоти, які, в свою чергу, використовуються в складних механізмах управління та оптимізації доходів. Більше того, практично всі програмні пакети управління запасами містять модулі, що виконують прогнози на основі того чи іншого типу ковзного середнього.

Розглянемо наступний приклад. Менеджеру потрібно спрогнозувати попит на вироблені його компанією верстати. Дані за обсягами продажів за останній рік роботи компанії знаходяться у файлі Станки.xls.

Просте ковзне середнє. У цьому методі середнє фіксованого числа N останніх спостережень використовується для оцінки наступного значення часового ряду. Наприклад, використовуючи дані про продажі верстатів за перші три місяці року, менеджер отримує для квітня значення

.

У разі довільного числа N вузлів розрахункова формула виглядає так

.

Менеджер обчислив обсяг продажів на основі простого ковзного середнього за 3 і 4 місяці. Але яка кількість вузлів дасть більш точний прогноз? Для оцінки точності прогнозів використовуються середнє абсолютних відхилень (САО) і середнє відносних похибок, у відсотках (СООП), які обчислюють за формулами

,

,

де N - кількість кроків прогнозу.

Згідно з результатами, отриманими на аркуші «Просте ковзне середнє» робочої книги Станки.xls (рис. 3), ковзне середнє за три місяці має значення САО рівне 12,67 (комірка D16), тоді як для змінного середнього за 4 місяці значення САО = 15,59 (комірка F16). Це означає, що використання більшої кількості статистичних даних швидше погіршує, ніж покращує точність прогнозу методом змінного середнього.

Рис. 3

На графіку (рис. 4), побудованому за результатами спостережень і прогнозів з інтервалом 3 місяці, можна помітити ряд особливостей, загальних для всіх застосувань методу ковзного середнього.

Рис. 4

Значення прогнозу, отримане методом простого ковзного середнього, завжди менше фактичного значення, якщо вихідні дані монотонно зростають, і більше фактичного значення, якщо вихідні дані монотонно спадають. Тому, якщо дані монотонно зростають або спадають, то за допомогою простого ковзного середнього неможна отримати точних прогнозів. Цей метод найкраще підходить для даних з невеликими випадковими відхиленнями від деякого постійного або повільно мінливого значення.

Основний недолік методу простого ковзного середнього виникає в результаті того, що при обчисленні прогнозованого значення саме останнє спостереження має таку ж вагу (тобто значущість), як і попередні. Це відбувається тому, що вага всіх N останніх спостережень, що беруть участь в обчисленні ковзного середнього, дорівнює 1/N. Присвоєння рівної ваги суперечить інтуїтивним відчуттям про те, що в багатьох випадках останні дані можуть більше сказати про те, що відбудеться в найближчому майбутньому, ніж попередні.

Зважене ковзне середнє. Внесок різних моментів часу можна врахувати, вводячи вагу для кожного значення показника в ковзному інтервалі. В результаті приходимо до методу зваженого ковзного середнього, який математично можна записати так

,

де - вага, з якою використовується показник при розрахунку.

Вага - це завжди додатне число. У випадку, коли всі ваги однакові, ми повертаємося до простого ковзного середнього.

Тепер наш менеджер може використовувати метод зваженого ковзного середнього за 3 місяці. Але як йому вибрати ваги? Звичайно, це завжди можна зробити «методом проб і помилок», вибираючи ваги довільно, і оцінюючи точність прогнозу за допомогою САО (САО менше, точність прогнозу вище). Проте, проби і помилки можуть тривати досить довго. Є простіший шлях.

Використовуючи засіб Пошук рішення, можна визначити оптимальну вагу вузлів. Щоб визначити вагу вузлів за допомогою засобу Пошук рішення, при якому значення середнього абсолютних відхилень було б мінімально, виконайте такі дії:

1. Виберіть команду Сервіс -> Пошук рішення.

2. У діалоговому вікні Пошук рішення установіть клітинку G16 цільової (див. лист «Веса») і вкажіть, що її значення повинне бути мінімальним.

3. У поле Змінюючи комірки введіть діапазон В1:В3.

4. Введіть обмеження В4 = 1,0, В1: ВЗ ≥ 0, В1: В3 ≤ 1, B1 ≤ В2 і В2 ≤ В3.

5. Натиснувши на кнопці Виконати, отримаєте результат, показаний на рис. 5.

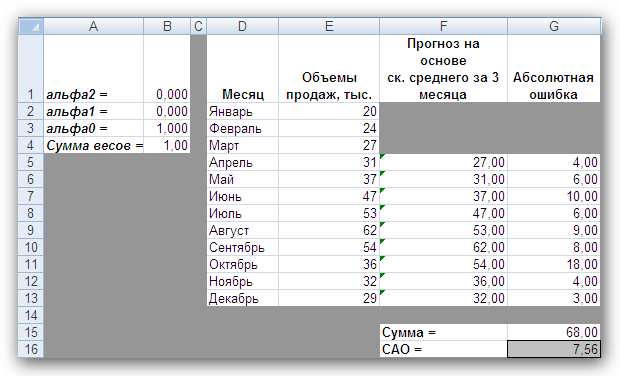
Рис. 5

Отримані результати показують, що оптимальний розподіл ваг такий, що вся вага зосереджена на самому останньому спостереженні, при цьому значення середнього абсолютного відхилення дорівнює 7,56. Цей результат підтверджує припущення про те, що більш пізні спостереження повинні мати більшу вагу.

Прогнози в методах ковзного середнього залежать від попередніх значень показника часового ряду, але не від якості попередніх прогнозів. Розглянемо один з методів прогнозування, який враховує відхилення попереднього прогнозу від реального значення показника ряду.

Метод експоненціального згладжування. Очевидно, що в методі зваженого ковзного середнього існує безліч способів задавати значення ваг так, щоб їх сума була рівною 1. Один з таких способів називається експоненціальним згладжуванням. У цій схемі методу зваженого середнього для будь-якого t > 1 прогнозоване значення в момент часу t +1 представляє собою зважену суму фактичного обсягу продажів, за період часу t і прогнозованого обсягу продажів, за період часу t. Іншими словами,

. (1)

Експоненціальне згладжування має обчислювальні переваги перед ковзним середнім. Тут, щоб обчислити , необхідно знати лише значення , і , (а також значення α), замість значень показника ряду у всіх вузлах, за якими відбувається згладжування. Зберігаючи значення α і останній прогноз, ми також неявно зберігаємо і всі попередні прогнози.

Розглянемо деякі властивості моделі експоненціального згладжування. Для початку зауважимо, що якщо t > 2, то у формулі (1) t можна замінити на t - 1, тобто підставивши цей вираз в первісну формулу (1), отримаємо

.

Виконуючи послідовно аналогічні підстановки, одержимо такий вираз для

.

Оскільки з нерівності 0 < α < 1 випливає, що 0 < 1 - α <1, то Іншими словами, спостереження має більшу вагу, ніж спостереження яке, в свою чергу, має більшу вагу, ніж . Це ілюструє основну властивість моделі експоненціального згладжування - коефіцієнти при спадають при зменшенні номера k. Також можна показати, що сума всіх коефіцієнтів (включаючи коефіцієнт при ), дорівнює 1.

З наведеної формули видно також, що значення є зваженою сумою всіх попередніх спостережень (включаючи останнє спостереження). Останній доданок цієї суми є не статистичним спостереженням, а «припущенням» (можна припустити, наприклад, що ). Очевидно, що з ростом t вплив , на прогноз зменшується, і в певний момент ним можна буде знехтувати. Навіть якщо значення α достатньо мале (таке, що (1 - α) приблизно дорівнює 1), значення буде швидко спадати.

Значення параметра α сильно впливає на функціонування моделі прогнозування, оскільки α являє собою вагу самого останнього спостереження. Це означає, що слід призначати більше значення α в тому випадку, коли в моделі найбільш прогностичним є саме останнє спостереження. Якщо ж α близько до 0, це означає практично повну довіру до минулого прогнозу та ігнорування останнього спостереження.

Перед менеджером виникає проблема: як найкращим чином підібрати значення α? У цьому допоможе засіб Пошук рішення. Щоб знайти оптимальне значення α (тобто таке, при якому прогнозна крива буде найменше відхилятися від кривої значень часового ряду), виконайте наступні дії.

1. Виберіть команду Сервіс -> Пошук рішення.

2. У діалоговому вікні Пошук рішення установіть цільову комірку G16 (див. лист «Експо») і вкажіть, що її значення повинне бути мінімальним.

3. Вкажіть, що змінною коміркою є комірка В1.

4. Введіть обмеження В1> 0 і B1 <1

5. Натиснувши на кнопці Виконати, отримаєте результат, показаний на рис. 6.

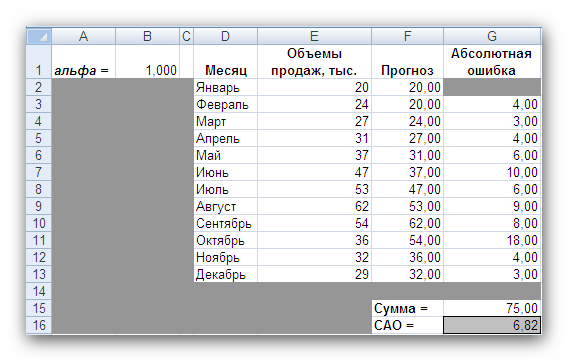
Рис. 6

Знову, як і в методі зваженого ковзного середнього, найкращий прогноз буде отриманий, якщо призначити всю вагу останньому спостереженню. Отже, оптимальне значення α дорівнює 1, при цьому середнє абсолютних відхилень дорівнює 6,82 (комірка G16).

Метод експоненціального згладжування добре працює в ситуаціях, коли змінна, що нас цікавить, поводиться стаціонарно, а її відхилення від постійного значення викликані випадковими факторами і не носять регулярного характеру. Але цим методом, як і методами ковзного середнього не вдасться спрогнозувати монотонно зростаючі або монотонно спадаючі дані. Прогнозовані значення будуть завжди менше або більше спостережуваних, відповідно, а точність даних буде порівнянна з точністю «наївного прогнозу». Ці методи також не враховують сезонних змін показника ряду.

Якщо статистичні дані монотонно змінюються або піддані сезонним змінам, необхідні спеціальні методи прогнозування, які будуть розглянуті нижче.

Підбір кривої тренду. Як приклад, скористаємося даними обсягів продажів з файлу Продажі.xls. Спочатку побудуємо точкову діаграму, що відображає реальні обсяги продажів. Щоб тепер побудувати за цими даними лінію тренда, що відображає тенденцію в зміні обсягів продажів, треба виконати такі дії.

1. Клацніть на будь-якій точці обраного ряду даних. В результаті будуть виділені всі точки ряду.

2. Клацніть правою кнопкою, і в меню виберіть Додати лінію тренда.

3. У діалоговому вікні Лінія тренда за замовчуванням буде обраний лінійний тип функції.

4. Клацніть на кнопці ОК.

Після цього на графіку з'явиться пряма лінія тренду (рис. 7).

Рис. 7

Для того щоб здійснити прогноз, потрібно в діалоговому вікні Лінія тренда вказати інтервал часу, що нас цікавить в пункті вперед на (або назад на).

В меню Лінія тренда можна також задати параметри кривої, що підбирається. Наприклад, він може бути експоненціальним або поліномом заданого ступеня.

У нашому випадку кривої тренду є пряма лінія з рівнянням . Коефіцієнти і для цієї кривої можна також знайти за допомогою надбудови Пакет Аналізу, вибравши засіб Регресія.

Метод Хольта - являє собою розвиток методу експоненціального згладжування, з урахуванням наявності тренда. Формулювання методу має вид

,

де

,

.

Метод Хольта дозволяє прогнозувати на k періодів часу вперед. Метод, як видно, використовує два параметри α і β, значення яких знаходяться в межах від 0 до 1. Змінна L, вказує на довгостроковий рівень значень або базове значення даних часового ряду. Змінна Т вказує на можливе зростання або спадання значень за один період, тобто на присутність тренда.

Розглянемо роботу цього методу на наступному прикладі. Світлана працює аналітиком у великій брокерській фірмі. На основі наявних у неї квартальних звітів компанії Startup Airlines вона хоче спрогнозувати дохід цієї компанії в наступному кварталі. Наявні дані та діаграма, побудована на їх основі, знаходяться в файлі Startup.xls (рис. 8). Видно, що дані мають явний тренд (майже монотонно зростають). Світлана хоче застосувати метод Хольта, щоб спрогнозувати значення прибутку на одну акцію на тринадцятий квартал. Для цього необхідно задати початкові значення для L і Т. Є кілька варіантів вибору: 1) L дорівнює значенню прибутку на одну акцію за перший квартал і T = 0,2) L дорівнює середньому значенню прибутку на одну акцію за 12 кварталів і T дорівнює середньому зміни за всі 12 кварталів. Існують й інші варіанти початкових значень для L і Т, але Світлана вибрала перший варіант.

Вона вирішила скористатися засобом Пошук рішення, щоб знайти оптимальне значення параметрів α і β, при яких значення середнього абсолютних помилок у відсотках було б мінімально. Для цього потрібно виконати такі дії.

1. Вибрати команду Сервіс -> Пошук рішення.

2. У діалоговому вікні Пошук рішення задати клітинку F18 цільовою і вказати, що її значення слід мінімізувати.

3. У поле Змінюючи комірки ввести діапазон комірок В1:В2. Додати обмеження В1: 2>0 і В1: В2<1.

4. Клацнути на кнопці Виконати.

Отриманий прогноз зображений на рис. 9, 10. Як видно, оптимальними виявилися значення α = 0,59 і β = 0,42, при цьому середня абсолютних похибок у відсотках дорівнює близько 38%.

Рис. 8

Рис. 9

 

Рис. 10

Однак метод Хольта, як і розглянуті раніше найпростіші методи прогнозування, не враховує наявність в часовому ряді сезонних змін.

Врахування сезонних змін. Попит на значне число товарів змінюється протягом року. Наприклад, якщо подивитися на обсяги продажів морозива по місяцях, то можна побачити в теплі місяці (з червня по серпень в північній півкулі) більш високий рівень продажів, ніж взимку, і так щороку. Тут сезонні коливання мають період в 12 місяців. Інший приклад: аналізуються щотижневі звіти про кількість постояльців, які залишалися на ніч в готелі, розташованому в бізнес-центрі міста. Приблизно можна сказати, що велика кількість клієнтів очікується в ночі на вівторок, середу і четвер, найменше клієнтів буде в ночі на суботу та неділю, і середнє число постояльців очікується в ночі на п'ятницю і понеділок. Така структура даних, що відображає кількість клієнтів в різні дні тижня, буде повторюватися через кожні сім днів.

Подібні циклічні зміни показника часового ряду носять назву сезонних коливань (хоча сезон, як ми бачили, може тривати і тиждень і рік). Процедура, яка дозволяє зробити прогноз з урахуванням сезонних змін, складається з наступних етапів.

1. На основі вихідних даних визначається структура сезонних коливань і період цих коливань.

2. Використовуючи числовий метод, описаний далі, з вихідних даних виключають сезонну складову.

3. На основі даних, з яких виключена сезонна складова, робиться найкращий можливий прогноз.

4. До отриманого прогнозу додається сезонна складова.

Проілюструємо цей підхід на даних про обсяги збуту вугілля (вимірюваного в тисячах тонн) в США протягом дев'яти років. Нехай Френк працює менеджером в компанії Gillette Coal Mine, і йому необхідно спрогнозувати попит на вугілля на найближчі два квартали. Він ввів дані по всій вугільній галузі в робочу книгу Уголь.xls і побудував за цими даними графік (рис. 11).

Визначення структури та періоду сезонних коливань. З графіка на рис. 11 видно, що обсяги продажів вище середнього рівня в першому і четвертому кварталах (зимовий час року) і нижче середнього в другому і третьому кварталах (весняно-літні місяці).

Рис. 11

Виключення сезонної складової. Спочатку необхідно обчислити середнє значення всіх відхилень за один період сезонних змін. Щоб виключити сезонну складову в межах одного року, використовуються дані за чотири періоди (квартали). А щоб виключити сезонну складову з усього часового ряду, обчислюється послідовність ковзних середніх за T вузлам, де T - тривалість сезонних коливань. Для виконання необхідних обчислень Френк використовував стовпці С і D, як показано на рис. нижче. Стовпець С містить значення ковзного середнього по 4 вузлам на основі даних, які знаходяться в стовпці В.

Тепер треба присвоїти отримані значення ковзного середнього середнім точкам послідовності даних, на основі яких ці значення були обчислені. Ця операція називається центруванням значень. Якщо T непарне, то перше значення ковзного середнього (середнє значень від першої до T-ї точки) треба присвоїти (T + 1) / 2 точці (наприклад, якщо T = 7, то перше ковзне середнє буде призначено четвертої точці). Аналогічно середнє значень від другої до (T + 1)-ї точки центрується в (T + 3) / 2 точці і т. д. Центр n-го інтервалу знаходиться в точці (T + (2n-1)) / 2.

Якщо T непарне, як в даному випадку, то завдання дещо ускладнюється, оскільки тут центральні (середні) точки розташовані між точками, за якими обчислювалося значення ковзного середнього. Тому центрування значення для третьої точки обчислюється як середнє першого і другого значень ковзного середнього. Наприклад, перше число у стовпці D відцентровані середніх на рис. 12, ліворуч дорівнює (1613 + 1594) / 2 = 1603.

 

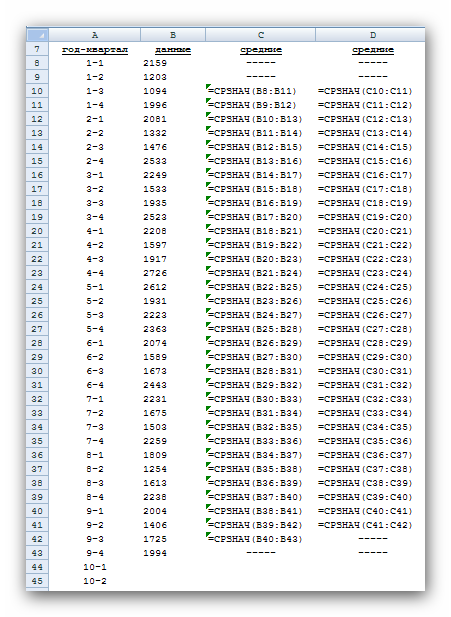
Рис. 12

На рис. 13 показані графіки вихідних даних і відцентрованих середніх.

Рис. 13

Далі знаходимо відношення значень точок даних до відповідних значень відцентрованих середніх (рис. 14). Оскільки точкам на початку і кінці послідовності даних немає відповідних відцентрованих середніх (див. перші і останні значення в стовпці D), така дія на ці точки не поширюється. Ці відносини показують ступінь відхилення значень даних щодо типового рівня, обумовленого відцентрованими середніми. Зауважимо, що значення відношення для третіх кварталів менше 1, а для четвертих - більше 1.

 

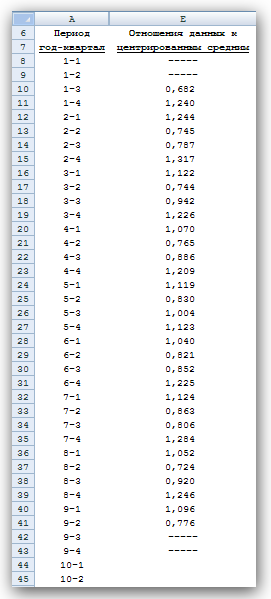
Рис. 14

Ці відношення є основою для створення сезонних індексів. Для їх обчислення групуються обчислені відношення по кварталах, як показано на рис. 15 в стовпцях G-О.

Рис. 15

Потім знаходяться середні значення відношень по кожному кварталу (стовпець Е на рис. 15). Наприклад, середнє всіх відношень для першого кварталу дорівнює 1,108. Це значення є сезонним індексом першого кварталу, на основі якого можна зробити висновок, що обсяг збуту вугілля за перший квартал становить у середньому близько 110,8% відносного середнього річного обсягу збуту.

Сезонний індекс - це середнє відношення даних, які стосуються одного сезону (в даному випадку сезоном є квартал), до всіх даних. Якщо сезонний індекс більше 1, значить, показники цього сезону вище середніх показників за рік, аналогічно, якщо сезонний індекс нижче 1, то показники сезону нижче середніх показників за рік.

Нарешті, щоб виключити з вихідних даних сезонну складову, слід поділити значення вихідних даних на відповідний сезонний індекс. Результати цієї операції наведені у стовпцях F і G (рис. 16). Графік даних, які вже не містять сезонної складової, представлений на рис. 17.

 

Рис. 16

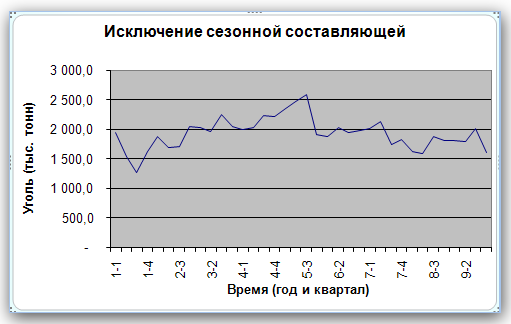
Рис. 17

Прогнозування без сезонної складової. На основі даних, з яких виключена сезонна складова, будується прогноз. Для цього використовується відповідний метод, який враховує характер поведінки даних (наприклад, дані мають тренд або відносно постійні). У цьому прикладі прогноз будується за допомогою простого експоненціального згладжування. Оптимальне значення параметра α знаходиться за допомогою засобу Пошук рішення. Графіки прогнозу та реальних даних з виключеною сезонної складової наведено на рис. 18.

Рис. 18

Врахування сезонної структури. Тепер потрібно врахувати в отриманому прогнозі (1726,5) сезонну складову. Для цього слід помножити 1726 на сезонний індекс першого кварталу 1,108, в результаті чого отримаємо значення 1912. Аналогічна операція (множення 1726 на сезонний індекс 0,784) дасть прогноз на другий квартал, що дорівнює 1353. Результат додавання сезонної структури до отриманого прогнозу показаний на рис. 19.

Рис. 19

Завдання

№ в журналі	Номери задач	№ в журналі	Номери задач	№ в журналі	Номери задач
1	1, 3	10	5, 12	19	13, 8
2	2, 14	11	1, 15	20	2, 12
3	6, 12	12	2, 8	21	4, 16
4	5, 8	13	1, 12	22	9, 11
5	7, 9	14	7, 10	23	3, 10
6	5, 7	15	8, 11	24	5, 8
7	8,10	16	9, 12	25	16, 9
8	9,11	17	4, 7	26	7, 10
9	10, 11	18	3, 4	27	8, 9

Завдання 1

Дано часовий ряд

t	1	2	3	4	5	6	7	8	9	10
x	57	40	35	33	56	46	45	26	26	53

1. Побудуйте графік залежності x = x (t).

2. Використовуючи просте ковзне середнє за 4 вузлами, спрогнозуйте попит в 11-й момент часу.

3. Знайдіть середнє абсолютних відхилень.

4. Чи підходить такий метод прогнозування для цих даних чи ні? Чому?

5. Чи є ця наближення кращим по відношенню до простого ковзного середнього по 3 вузлів? Чому?

6. Підберіть лінійну функцію наближення даних методом найменших квадратів.

7. Скористайтеся для прогнозу методом експоненціального згладжування. Який із використаних методів дає кращий результат?

Завдання 2

Користуючись моделлю прогнозів доходів компанії Startup Airlines (Startup.xls) виконайте:

1. Побудуйте прогноз значень прибутку за допомогою зваженого ковзного середнього по 4 вузлам. Підберіть оптимальні значення ваг вузлів за допомогою засобу Пошук рішення.

2. Побудуйте прогноз значень прибутку за допомогою методу експоненціального згладжування. Визначте за допомогою засобу Пошук рішення оптимальне значення .

3. Побудуйте лінію тренда.

4. Порівняйте точність побудованих прогнозів з прогнозом, отриманим по методу Хольта. Який з методів дає більш точніші результати?

Завдання 3

Для часового ряду

t	1	2	3	4	5	6	7	8	9	10
x	50	40	37	33	56	46	45	29	26	53

виконайте:

1. Використовуючи зважене ковзне середнє з 4 вузлів, і призначивши ваги 4/10, 3/10, 2/10, 1/10, спрогнозуйте попит в 11-й момент часу. Більшу вагу слід призначати більш пізнім спостереженням.

2. Чи є це наближення кращим по відношенню до простого ковзного середнього по 4 вузлам? Чому?

3. Знайдіть середнє абсолютних відхилень.

4. За допомогою засобу Пошук рішення знайдіть оптимальні ваги вузлів. Наскільки зменшилася помилка наближення?

5. Скористайтеся для прогнозу методом експоненціального згладжування. Який із використаних методів дає кращий результат?