
2 курс вища математика / Функ компл змінної методичка
.pdfМіністерство освіти і науки України Київський національний університет технологій та дизайну
ВИЩА МАТЕМАТИКА
Функції комплексної змінної
МЕТОДИЧНІ ВКАЗІВКИ ТА ЗАВДАННЯ ДЛЯ САМОСТІЙНОЇ РОБОТИ СТУДЕНТІВ
ІІ-ГО КУРСУ
Затверджено на засіданні кафедри
вищої математики Протокол № 8
від 19. 03. 2008 р.
Київ КНУТД 2008
Вища математика. Функції комплексної змінної. Методичні вказівки та завдання для самостійної роботи студентів ІІ-го курсу.
/ Упор.: М.О. Харитонова, О.О. Мазурок. – К.: КНУТД, 2008 . – 60 с.
Упорядники: М.О. Харитонова, доцент, О.О. Мазурок, доцент.
Відповідальний за випуск зав. кафедрою вищої математики Задерей П.В.
2
ЕЛЕМЕНТИ ТЕОРІЇ ФУНКЦІЙ КОМПЛЕКСНОЇ ЗМІННОЇ
1. Поняття про комплексні числа.
Комплексним числом називається вираз:
z = a + b ×i [1],
де a та |
b – дійсні числа, а символ i |
– уявна одиниця, яка визначається |
||||
умовою: |
i2 = −1. При цьому число |
a називається дійсною частиною ком- |
||||
плексного числа z і позначається: |
a = Re z , а b – уявною частиною z , |
|||||
b = Im z (від французьких слів: гееl – дійсний, іmаgіпаіге – уявний). |
||||||
Вираз, що стоїть справа у формулі |
[1], називається алгебраїчною фор- |
|||||
мою запису комплексного числа. |
|
|
z = a - b ×i, |
|
||
Два комплексні числа |
z = a + b ×i |
і |
які відрізняються |
|||
лише знаком уявної частини, називаються спряженими. |
|
|||||
Два комплексні числа |
z1 = a1 |
+ b1 ×i |
і |
z2 = a2 + b2 ×i |
вважаються рів- |
|
ними ( z1 = z2 ) тоді і тільки тоді, коли рівні їхні дійсні частини і рівні їхні уявні частини:
Комплексне число z = a + b ×i дорівнює нулю ( z = a + b ×i = 0 ) тоді і тільки тоді, коли a = b = 0.
Комплексні числа можна зображати на площині.
Якщо користуватись декартовою системою координат, то число [1] зображається точкою M (a;b). Така площина називається комплексною площиною
змінної z , вісь Ox – дійсною віссю, |
а Oy – уявною. |
Комплексне число z = a + b ×i |
при b = 0 збігається з дійсним чис- |
лом a : z = a + 0 ×i = a. Тому дійсні числа є окремим випадком комплексних, вони зображаються точками осі Ox .
Комплексні числа z = a + b ×i , в яких a = 0 , називаються суто уявними; такі числа зображаються точками осі Oy .
Допускається запис комплексного числа у вигляді:
Основні дії над комплексними числами z1 = a1 + b1 ×i і z2 = a2 + b2 ×i ,
заданими в алгебраїчній формі, визначаються такими рівностями:
1)z1 + z2 = (a1 + a2 ) + (b1 + b2 ) ×i ;
2)z1 - z2 = (a1 - a2 ) + (b1 - b2 ) ×i;
3)z1 × z2 = (a1a2 - b1b2 ) + (b1a2 + a1b2 ) ×i ;
4) |
z1 |
= |
z1 × z2 |
= |
a1a2 + b1b2 |
+ |
a2b1 |
- a1b2 |
×i . |
|||||
z |
2 |
z |
2 |
× z |
2 |
a |
2 + b 2 |
a 2 |
+ b 2 |
|||||
|
|
|
|
|
|
2 |
2 |
|
2 |
2 |
|
|||
Таким чином, арифметичні дії над комплексними числами виконуються за звичайними правилами дій над двочленами з урахуванням того, що i2 = -1.
3

Приклад 1.1 |
Обчислити: |
(1+ 5i)×(2 - 3i)-15 + 2i . |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||
↓. (1+ 5i)×(2 - 3i)-15 + 2i = |
|
|
|
4 + i |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||
2 - 3i +10i +15 -15 + 2i |
= |
|
2 + 9i |
= |
|
|||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
4 + i |
|
|
|
|
|
|
|
|
|
|
4 + i |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
4 + i |
|
||||
(2 + 9i)×(4 - i) |
8 - 2i + 36i + 9 |
|
17 + 34i |
=1+ 2i . |
|
|
|
|
|
|
|
|
|
|
|
1+ 2i . |
||||||||||||||||||||||||
= (4 + i)×(4 - i) = |
|
|
|
|
|
|
|
|
= |
|
|
|
|
|
|
↑. |
|
|
|
|
|
Відп.: |
||||||||||||||||||
|
16 +1 |
|
|
|
17 |
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||
Піднесення числа |
z = a + b ×i |
|
до цілого натурального степеня вико- |
|||||||||||||||||||||||||||||||||||||
нується за формулою бінома Ньютона з урахуванням того, що: |
|
|||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
i2 |
= -1, i3 |
= -i, |
|
i4 =1, |
|
i5 |
= i , ... . |
|
|
|
|
|
|
|
|
|
|
|||||||||||||
Полярні координати точки M (x; y) на комплексній площині назива- |
||||||||||||||||||||||||||||||||||||||||
ються модулем і аргументом комплексного числа |
|
z = x + y ×i |
і позначають- |
|||||||||||||||||||||||||||||||||||||
ся: ρ = |
|
|
z |
|
|
= |
|
|
|
|
|
ϕ = Argz . |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
x2 + y2 |
, |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||
Оскільки |
|
|
|
|
|
|
x = ρ ×cosϕ , |
y = ρ ×sinϕ |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||
(див. рисунок), то з формули [1] маємо: |
y |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
M |
||||||||||||||||||||||
z = ρ ×(cosϕ + i ×sinϕ) |
[2]. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||
Вираз, який стоїть справа у формулі [2], |
|
|
|
|
|
|
|
|
|
|
ρ |
|
|
|
|
|
|
|
|
|||||||||||||||||||||
називається тригонометричною формою |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
x |
||||||||||||||||||||
комплексного числа |
z = x + y ×i . |
|
|
|
Î |
|
|
|
ϕ |
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||
|
|
|
|
|
|
|
= ρ комплексного |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
Модуль |
|
|
z |
|
z числа визначається однозначно, |
|
||||||||||||||||||||||||||||||||||
|
|
|
|
|||||||||||||||||||||||||||||||||||||
|
|
|
|
|
а аргумент |
ϕ – з точністю до 2πk : |
|
Argz = arg z + 2πk , |
k Î Z . |
|||||||||||||||||||||||||||||||
Тут під Argz розуміють загальне |
|
|
ì |
|
|
|
y |
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||
значення аргументу; на відміну від |
|
|
ïarctg |
|
|
, |
|
|
x > 0; |
|
||||||||||||||||||||||||||||||
|
|
x |
|
|
||||||||||||||||||||||||||||||||||||
нього, arg z |
– головне значення ар- |
|
|
ï |
|
|
|
|
|
|
|
y |
|
|
|
|
|
|
|
|
||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||
гументу, воно знаходиться на про- |
|
|
ïπ + arctg |
|
, |
|
x < 0, y > 0; |
|||||||||||||||||||||||||||||||||
|
|
x |
|
|||||||||||||||||||||||||||||||||||||
міжку (-π ;π ] і відраховується від |
|
|
ï |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||
arg z = |
ï |
|
|
|
|
|
|
|
|
|
|
|
|
|
y |
|
|
|
|
|||||||||||||||||||||
додатного напряму осі Ox проти |
í-π + arctg |
|
|
|
, |
x < 0, y < 0; |
||||||||||||||||||||||||||||||||||
|
|
|
|
|||||||||||||||||||||||||||||||||||||
годинникової стрілки. |
|
|
|
|
|
|
|
|
|
|
ï |
|
|
|
|
|
|
|
|
|
|
|
|
|
x |
|
|
|
||||||||||||
Якщо z = 0, |
|
|
|
|
|
|
|
|
|
|
|
|
|
ïπ |
, x |
= |
|
0, y |
> |
0; |
|
|
||||||||||||||||||
то вважають, що |
|
z |
|
= 0, |
|
|
|
|
|
ï 2 |
|
|
|
|
|
|
|
|||||||||||||||||||||||
|
|
|
|
|
|
|
ï |
|
π |
, |
x = 0, y |
< 0. |
|
|||||||||||||||||||||||||||
|
|
|
|
|
|
|
а |
arg z – невизначений. |
|
|
|
|
||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
ï- |
2 |
|
|||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
î |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
Розглянемо дії над комплексними числами в тригонометричній формі.
Нехай z1 = ρ1 ×(cosϕ1 + i ×sinϕ1 ), z2 = ρ2 ×(cosϕ2 + i ×sinϕ2 ), тоді: z1 × z2 = ρ1 × ρ2 ×(cosϕ1 + i ×sinϕ1 )×(cosϕ2 + i ×sinϕ2 )=
=ρ1 × ρ2 ×[(cosϕ1 cosϕ2 - sinϕ1 sinϕ2 ) + (sinϕ1 cosϕ2 + cosϕ1 sinϕ2 ) ×i]=
=ρ1 × ρ2 ×[cos(ϕ1 +ϕ2 ) + sin(ϕ1 +ϕ2 ) ×i].
4

Отже, під час множення комплексних чисел їхні модулі перемножуються, а аргументи додаються.
Це правило поширюється на довільно скінченне число множників.
Зокрема, якщо всі |
n множників рівні, то справедлива формула Муавра:: |
||||||||
zn = (ρ ×(cosϕ + i ×sinϕ))n = ρ n ×(cos nϕ + i ×sin nϕ) [M]. |
|||||||||
При діленні комплексних чисел маємо: |
|
|
|||||||
|
z1 |
= |
|
ρ1 |
(cos(ϕ -ϕ |
) + i ×sin(ϕ -ϕ |
)) [M.1]. |
||
|
|
|
|||||||
|
z2 |
1 |
2 |
1 |
2 |
|
|||
|
|
ρ2 |
|
|
|
|
|||
Модуль частки двох комплексних чисел дорівнює частці модулів діленого і дільника; аргумент частки дорівнює різниці аргументів діленого і дільника.
|
При добуванні кореня n -го степеня з комплексного числа, записаного |
||||||||
в тригонометричній формі |
[2] користуються наступною формулою (наслі- |
||||||||
док з формули Муавра): |
|
|
|
|
|||||
n |
|
|
|
æ |
ϕ + 2πk |
+ i ×sin |
ϕ + 2πk ö |
[M.2], |
|
|
|
||||||||
z = n ρ ×çcos |
n |
n |
÷, k = 0,1, 2, ..., n −1 |
||||||
|
è |
|
ø |
|
|||||
де під коренем n ρ потрібно розуміти його арифметичне значення.
ρ потрібно розуміти його арифметичне значення.
Надаючи k значень |
0,1, 2, ..., n −1, |
дістанемо |
|
|
n |
|
|
|
|
різних значень кореня. |
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
Для інших значень |
|
k |
аргументи відрізнятимуться від знайдених на число, |
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
кратне 2π , тому значення кореня збігатимуться зі вже знайденими. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
Приклад 1.2 Знайти всі значення кореня: |
|
4 |
|
|
|
|
|
. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||||||||||||||||
-1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
↓. Оскільки |
|
|
|
|
|
|
|
|
|
z = −1, то |
ρ =1, ϕ = π |
і згідно формули [M] |
|
отримаємо: |
|
|
|
|
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
æ |
|
|
π + 2π × 0 |
|
|
|
|
|
|
π + 2π × 0 ö |
|
|
|
|
|
π |
|
|
|
|
|
|
|
|
|
π |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||
k = 0 : z1 |
= 4 |
|
|
|
|
|
|
|
|
|
|
+ i × sin |
|
|
|
|
|
|
+ i × sin |
|
|
|
|
|
|
|
|
|
2 |
|
|
+ i |
|
|
|
|
|
|
|
2 |
|
|
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
1 × çcos |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
÷ = cos |
|
|
|
|
|
|
|
|
|
|
= |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
× |
|
|
|
|
|
|
|
|
|
|
|
|
; |
||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
4 |
|
|
|
|
|
|
|
|
|
|
4 |
|
|
|
|
4 |
|
|
|
4 |
|
|
2 |
|
|
|
2 |
|
|
|
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
è |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
ø |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
æ |
|
π + 2π ×1 |
|
|
|
|
|
π + 2π ×1 |
ö |
|
|
|
|
3π |
|
|
|
|
|
|
|
|
|
|
3π |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||
k =1: z2 |
= 4 |
|
|
|
|
|
|
|
+ i sin |
|
|
|
|
|
|
+ isin |
|
|
|
|
|
|
|
|
|
2 |
|
|
|
+ i |
|
|
|
2 |
|
|
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
1 × çcos |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
÷ = cos |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
= - |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
× |
|
|
|
|
|
|
|
|
|
|
|
|
; |
||||||||||||||||||||||||||||||||||||||
|
|
|
4 |
|
|
|
|
|
|
4 |
|
|
|
4 |
|
|
|
|
4 |
|
|
|
|
|
2 |
|
|
|
|
2 |
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
è |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
ø |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
æ |
|
π + 2π × 2 |
|
|
|
|
|
π + 2π × 2 ö |
|
5π |
|
|
|
|
|
|
|
|
|
5π |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||||||
k = 2 : z3 |
= 4 |
|
|
|
|
|
|
|
|
|
|
+ isin |
|
|
+ isin |
|
|
|
|
|
|
|
|
|
2 |
|
- i |
|
|
|
2 |
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
1 × çcos |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
÷ = cos |
|
|
|
|
|
|
|
|
|
|
|
|
|
= - |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
; |
|
|||||||||||||||||||||||||||||||||||||||||
|
|
|
4 |
|
|
|
|
|
|
|
|
4 |
|
|
|
4 |
|
|
|
4 |
|
|
|
|
2 |
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
è |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
ø |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
æ |
|
|
π + 2π × 3 |
|
|
|
|
π + 2π × 3 ö |
|
|
7π |
|
|
|
|
|
|
|
|
7π |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||||||||
k = 3: z4 |
= 4 |
|
|
|
|
|
|
|
|
+ i sin |
|
|
+ isin |
|
|
|
|
|
|
2 |
|
|
|
|
- i |
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
1 × çcos |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
÷ = cos |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
= |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||
|
|
|
|
4 |
|
|
|
|
|
|
|
4 |
|
|
4 |
|
|
|
4 |
|
|
|
|
|
|
2 |
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
è |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
ø |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||||
Відп.: |
|
|
2 |
|
+ i × |
|
|
2 |
|
, |
- |
|
|
|
2 |
|
+ i × |
|
|
|
|
2 |
|
, |
- |
|
|
|
2 |
|
- i × |
|
|
|
|
|
|
2 |
|
, |
|
|
|
2 |
|
|
= i × |
|
|
|
|
|
|
|
|
2 |
|
. |
|
|
|
↑. |
|
|
|
|
|
||||||||||||||||||||||||||||||||||
2 |
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
2 |
|
|
2 |
|
|
|
|
|
|
|
|
|
|
2 |
|
|
2 |
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
y |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||||
Як видно з рисунку, всі чотири корені знахо- |
|
|
|
|
|
|
|
|
|
|
z2 |
|
|
|
|
|
|
z1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
дяться на колі радіуса |
4 |
|
ρ |
|
|
|
|
з центром у по- |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||
чатку координат і є вершинами правильного |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
x |
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||||||||||||||
чотирикутника. Ця властивість справедлива |
|
|
|
|
|
|
|
|
|
|
z3 |
|
|
|
|
|
|
|
|
|
|
z4 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
для всіх коренів |
n -го степеня (n N ) з ком- |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
z = ρ ×(cosϕ + i ×sinϕ).
5

Приклад 1.3 Знайти множину точок z |
комплексної площини |
(z), що за- |
|||||||||
довольняють співвідношенню: Re(z2 - z)= 0 |
|
||||||||||
↓. Оскільки |
z = x + i × y , |
z = x - i × y , |
z2 = (x + iy)2 = x2 - y2 |
+ 2ixy , то: |
|||||||
Re(z2 - |
|
)= Re(x2 - y2 + 2xyi - x + yi)= x2 - y2 - x = 0; |
|
||||||||
z |
|
||||||||||
æ |
|
|
1 |
ö |
2 |
2 |
|
1 |
|
y |
|
тобто: ç x - |
|
÷ |
- y |
|
= |
|
, |
|
|||
2 |
|
4 |
|
||||||||
è |
|
|
ø |
|
|
|
|
|
|
||
æ |
1 |
ö2 |
|
|
2 |
|
|
|
звідки: 4 ×ç x - |
|
÷ |
- 4y |
|
=1 – |
|
|
|
2 |
|
A |
x |
|||||
è |
ø |
|
|
|
O |
|||
рівняння рівносторонньої гіперболи з |
Ñ |
|
||||||
|
|
æ 1 |
ö |
|
|
|
|
|
центром в точці |
Ñèç |
2 |
;0ø÷ |
|
і вершина- |
|
|
|
ми в точках: O(0;0) і A(1;0). |
↑. |
|
|
|
||||||||||||||||||
Відп.: гіпербола |
4(x - 0,5)2 - 4y2 =1. |
|
|
|
||||||||||||||||||
Приклад 1.4 Знайти множину точок z |
комплексної площини (z), що задо- |
|||||||||||||||||||||
вольняють умові: |
|
|
z - i |
|
+ |
|
z + i |
|
|
£ 4 |
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
|||||||||||||||
↓. Враховуючи, що z = x + yi , |
z − i = x + (y −1)i, z + i = x + (y +1)i , |
|||||||||||||||||||||
|
|
z - i |
|
|
|
|
, |
|
|
z + i |
|
= |
|
|
, |
|||||||
а також: |
|
|
= |
|
x2 + (y -1)2 |
|
|
|
x2 + (y +1)2 |
|||||||||||||
|
|
|
|
|||||||||||||||||||
знайдемо рівняння межі: 
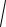 x2 + (y -1)2 +
x2 + (y -1)2 + 
 x2 + (y +1)2 = 4 Þ
x2 + (y +1)2 = 4 Þ
Þ 
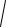 x2 + (y -1)2 = 4 -
x2 + (y -1)2 = 4 - 
 x2 + (y +1)2 Þ
x2 + (y +1)2 Þ
Þ x2 + (y -1)2 =16 - 8
 x2 + ( y +1)2 + x2 + (y +1)2 Þ
x2 + ( y +1)2 + x2 + (y +1)2 Þ
Þ 2
 x2 + (y +1)2 = 4 + y Þ 4x2 + 4y2 + 8y + 4 =16 + 8y + Þ 4x2 + 3y2 = 12 .
x2 + (y +1)2 = 4 + y Þ 4x2 + 4y2 + 8y + 4 =16 + 8y + Þ 4x2 + 3y2 = 12 .
Отже, лінія z - i + z + i = 4
визначає еліпс: |
|
x2 |
+ |
y2 |
=1 |
|
|
|
3 |
4 |
|||||||
|
|
|
|
|
||||
з центром у початку координат, |
||||||||
великою віссю |
b = 2 |
і малою віссю a = |
|
. |
||||
3 |
||||||||
Нерівність z − i + z + i ≤ 4 визначає внутрішню частину цього еліпса разом з межею. ↑.
y2 Þ
y
2
0 
 3 x
3 x
Відп.: внутрішня частина еліпса |
x2 |
+ |
y2 |
=1 разом з межею. |
3 |
|
|||
|
4 |
|
||
6

Приклад 1.5 Виразити sin 5x через sin x і cos x .
↓. Розглянемо комплексне число z = cos x + i ×sin x. Скориставшись формулою бінома Ньютона, отримаємо: z5 = (cos x + i ×sin x)5 =
= cos5 x + 5cos4 x ×i sin x -10cos3 x ×sin2 x -10cos2 x ×i sin3 x +
+ 5cos x ×sin4 x + i sin5 x = (cos5 x -10cos3 x ×sin2 x + 5cos x ×sin4 x)+ + i ×(5cos4 x ×sin x -10cos2 x ×sin3 x + sin5 x). [*]
А з формули Муавра відомо, що: z5 = cos5x + i ×sin 5x |
[**]. |
|||
Порівнявши дійсну і уявну складові правих частин в рівностях |
[*] |
і [**], |
||
отримаємо: |
sin 5x = 5cos4 x ×sin x -10cos2 |
x ×sin3 x + sin5 x |
|
|
і одночасно: |
cos5x = cos5 x -10cos3 x ×sin2 |
x + 5cos x ×sin4 x . |
↑. |
|
З формули Ейлера: cosϕ + i ×sinϕ = ei×ϕ |
(яку ми доведемо пізніше) |
|||
випливає, що комплексне число, записане у тригонометричній формі: z = ρ ×(cosϕ + i ×sinϕ), може бути також записане у вигляді:
z = ρ ×ei×ϕ [3] – показникова форма комплексного числа.
Операції над комплексними числами в показниковій формі:
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
i×ϕ |
|
|
|
|
|
i×ϕ |
|
|
|
|
|
|
|
|
|
i×çϕ +ϕ |
|
÷ |
|
||||
|
Множення: z × z |
|
|
= ρ |
|
|
×e |
1 |
× ρ |
|
×e |
|
2 |
|
= ρ |
|
× ρ |
|
æ |
1 |
2 |
ö |
|
||||||||||||||||||
1. |
2 |
1 |
|
2 |
|
|
1 |
2 |
×e è |
ø . |
|
||||||||||||||||||||||||||||||
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
i×ϕ |
|
|
|
|
|
|
|
|
i×çϕ -ϕ |
|
÷ |
|
|
|
|
|
|
|
|
|
|
||||||||
|
|
|
|
|
z1 |
|
ρ1 ×e |
|
|
1 |
|
|
|
|
ρ1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
æ |
|
|
|
|
ö |
|
|
|
|
|
|
|
|
|
|
|||||||||
2. |
Ділення: |
= |
|
|
|
|
|
|
= |
|
×e è 1 |
|
2 |
ø . |
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||
|
|
|
|
|
|
i×ϕ2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||
|
|
|
|
|
z2 |
ρ2 |
×e |
|
|
|
|
ρ2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
n |
|
|
|
|
|
|
|
|
|
n |
|
|
|
|
|
|
|
|
|
|||||||
3. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
× |
|
|
|
|
|
|
× × |
|
|
|
|
|||||
Піднесення до степеня: (z) |
= (ρ ×ei |
ϕ ) = ρn |
×ei nϕ . |
|
|
|
|||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
ϕ |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
4. |
Добування кореня: n |
|
|
= n ρ ×ei×ϕ = n |
|
×ei×n , де ϕ = arg z + 2πk , |
|||||||||||||||||||||||||||||||||||
z |
ρ |
||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
arg z+2πk |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
тобто: |
n |
|
= n |
|
×ei× |
|
n |
|
|
, |
|
k = 0, 1, 2, |
..., n −1. |
||||||||||||||||||||||||
|
|
|
|
z |
ρ |
|
|
|
|
||||||||||||||||||||||||||||||||
Приклад 1.6 |
Обчислити ii . |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||
↓. Представимо основу степеня в показниковій формі: |
|
|
|
|
|||||||||||||||||||||||||||||||||||||
|
æ |
π |
|
ö |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
æ |
|
æπ |
|
|
|
|
|
|
ö |
öi |
|
æπ |
|
|
ö |
||||||
|
i×ç |
2 |
+ 2πk ÷ |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
ç |
i ×ç |
|
+ 2πk ÷ |
÷ |
|
|
ç |
+2πk |
÷ |
|||||||||||||
i =1×e è |
|
|
|
ø , k Z Þ ii = |
çe |
|
è 2 |
|
|
|
|
|
|
ø |
÷ |
|
= e-è 2 |
ø , k Z .↑. |
|||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
ç |
|
|
|
|
|
|
|
|
|
|
|
÷ |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
ç |
|
|
|
|
|
|
|
|
|
|
|
÷ |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
è |
|
|
|
|
|
|
|
|
|
|
|
ø |
|
|
|
|
|
|
|
Відп.: нескінченна множина дійсних чисел: |
|
e−π2 , |
e−π2 ±2π , |
e−π2 ±4π , . |
|||||||||||||||||||||||||||||||||||||
7
|
|
|
2. Функції комплексної змінної. |
D комплек- |
||||||
Якщо кожному значенню змінної z = x + i × y із області |
||||||||||
сної площини |
(z) |
за правилом |
ω = f (z) |
ставиться у відповідність зна- |
||||||
чення ω = u + i ×v |
із області E комплексної площини (ω), то |
ω = f (z) |
||||||||
називають комплексною функцією комплексної змінної |
z ; |
|
||||||||
D – область визначення, |
E – область значень функції |
f (z) . |
|
|||||||
Залежність ω = f (z) може бути записана у вигляді: |
|
|||||||||
|
|
ω = u(x, y) + i ×v(x, y) = Re f (z) + i × Im f (z), |
|
|||||||
де u(x, y) та |
v(x, y) – дійсні функції двох дійсних змінних x |
та y . |
||||||||
Функція |
u(x, y) = Re f (z) |
називається дійсною частиною функції |
||||||||
ω = f (z) , а |
|
v(x, y) = Im f (z) – уявною частиною цієї функції. |
||||||||
Приклад 2.1 |
Виділити дійсну та уявну частини функції f (z) = z - i × z2 . |
|||||||||
↓. Оскільки |
z = x + i × y , |
z = x - i × y , z2 |
= (x + iy)2 = x2 − y2 + 2ixy , то: |
|||||||
f (z) = x - iy - i ×(x2 - y2 |
+ 2ixy)= x + 2xy + i ×(y2 - x2 - y). ↑. |
|||||||||
Відп.: u(x, y) = Re f (z) = x + 2xy , v(x, y) = Im f (z) = y2 - x2 - y . |
||||||||||
Границя та неперервність функції |
f (z) визначаються аналогічно |
|||||||||
відповідним поняттям для функції дійсної змінної. |
|
|
||||||||
Запис |
lim f (z) = A, |
|
|
|
|
|
||||
|
z→z0 |
|
|
|
|
|
|
|
|
|
де f (z) = u(x, y) + i ×v(x, y), z0 = x0 + i × y0 , A = α + i × β , |
|
|||||||||
рівносильний такому: |
lim u(x, y) = α |
та |
lim v(x, y) = β . |
|
||||||
|
|
|
|
x→x |
|
|
x→x |
|
|
|
|
|
|
|
y→y0 |
|
|
y→y0 |
|
|
|
|
|
|
|
|
0 |
|
|
0 |
|
|
Функція |
f (z) = u(x, y) + i ×v(x, y) |
неперервна в точці z0 , якщо фу- |
||||||||
нкції u(x, y) |
та v(x, y) |
неперервні в точці |
(x0 , y0 ) |
як функції двох дійс- |
||||||
них змінних |
x та |
y . |
Функція |
f (z) називається неперервною в області, |
||||||
якщо вона неперервна в кожній точці цієї області.
Нехай задано ряд з комплексними членами:
∞
z1 + z2 + ... + zn + ... = å zn , де
n=1
Сума Sn = z1 + z2 + ... + zn називається
Якщо існує скінчена границя lim
n→∞
zk = xk + i × yk , k =1, 2, 3, ....
∞
частинною сумою ряду å zn .
n=1
Sn = S ,
∞ |
∞ |
то ряд å zn |
називають збіжним, а число S = å zn – сумою ряду. |
n=1 |
n=1 |
8

¥
Ряд å zn , zk = xk + i × yk , k =1, 2, 3, ... є збіжним тоді і тільки тоді,
n=1
коли є збіжними ряди:
x1 + x2 + ...+ xn |
|
|
∞ |
|
y1 |
+ y2 + ...+ yn |
∞ |
|||
+ ... = å xn |
і |
+ ... = å yn ; |
||||||||
|
|
|
n=1 |
|
|
|
∞ |
|
n=1 |
|
Ряд виду: c |
+ c × z + c |
|
× z2 |
+ ... + c |
|
|
|
× zn , |
||
2 |
n |
× zn + ... = åc |
n |
|||||||
0 |
1 |
|
|
|
|
n=0 |
|
|||
|
|
|
|
|
|
|
|
|
|
|
де ci (i = 0,1, 2,...) – комплексні числа, |
а |
|
z – комплексна змінна, |
|||||||
називається степеневим рядом в комплексній області.
Основні елементарні функції комплексної змінної.
1) Ціла раціональна функція (многочлен n -го степеня):
n
ω = Pn (z) = å ak × zk = a0 + a1 × z + a2 × z2 + ... + an × zn ,
k=0
де ak – комплексні коефіцієнти, an ¹ 0 .
2)Дробово-раціональна функція (частка двох многочленів):
ω= Pn (z) = a0 + a1 × z + a2 × z2 + ... + an × zn . Qm (z) b0 + b1 × z + b2 × z2 + ... + bm × zm
3)Тригонометричні функції sin z та cos z визначаються степеневими рядами:
ω = sin z = z - z |
3 |
|
+ z |
5 |
|
- z |
7 |
|
+ ... = å (-1) |
k |
|
|
|
× z2k+1 |
, z < ¥ |
[4]; |
|
||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
¥ |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
3! |
|
|
|
5! |
|
|
|
7! |
|
|
k=0 |
(2k +1)! |
|
|
|
|
|
|
|
|
|
[5]. |
|
|
|||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
z < ¥ |
|
|
||||||||||||||||||||
ω = cos z =1- z |
2 |
|
+ z |
4 |
|
- z |
6 |
+ ... = å |
(-1) |
k |
× z2k , |
|
|
|
|||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
¥ |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2! |
|
|
|
|
4! |
|
|
|
|
6! |
k=0 |
(2k)! |
|
|
|
sin z |
|
|
|
|
|
|
|
cos z |
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||
Функції tgz та ctgz за означенням рівні: ω = tgz = |
|
; ω = ctgz = |
. |
||||||||||||||||||||||||||||||||
cos z |
|
||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
sin z |
|||
4) Натуральна показникова функція |
|
ω = ez |
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||
(показникова функція за основою e) визначається степеневим рядом: |
||||||||||||||||||||||||||||||||||||||||||||
ω = ez =1+ z + z |
2 |
|
+ z |
3 |
+ z |
4 |
|
+ z |
5 |
|
+ z |
+ ... = |
|
å z |
k |
, |
|
z < ¥ |
[6]. |
|||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
6 |
|
|
|
|
¥ |
|
|
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1! 2! 3! 4! 5! 6! |
|
|
|
|
k=0 |
k! |
|
|
|
|
|
|||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||
Між натуральною показниковою функцією |
ez |
|
і тригонометричними |
|||||||||||||||||||||||||||||||||||||||||
функціями |
sin z |
|
та |
cos z |
існує простий зв’язок. Підставимо в ряд |
[6] зна- |
||||||||||||||||||||||||||||||||||||||
чення i × z |
замість |
z |
|
і згрупуємо окремо доданки, які містять множник i і |
||||||||||||||||||||||||||||||||||||||||
які цього множника не містять: |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||
ei×z =1+ |
i × z |
|
+ (i × z)2 + (i × z)3 |
|
+ (i × z)4 + (i × z)5 |
+ |
(i × z)6 |
+ (i × z)7 |
... = |
|||||||||||||||||||||||||||||||||||
|
|
|
|
|
6! |
|||||||||||||||||||||||||||||||||||||||
|
1! |
|
|
|
|
2! |
|
|
|
|
|
3! |
|
|
|
|
|
|
|
4! |
|
|
|
5! |
|
|
|
|
|
7! |
|
|||||||||||||
|
=1+ i × |
z |
|
- |
z2 |
|
- i × |
z3 |
|
|
+ |
z4 |
|
|
+ i × |
z5 |
- |
z6 |
|
- i × |
z7 |
+ ... = |
|
|||||||||||||||||||||
|
|
|
|
|
|
|
|
|
5! |
|
|
|
||||||||||||||||||||||||||||||||
|
|
|
|
1! |
|
2! |
|
|
|
3! |
|
4! |
|
|
|
|
6! |
|
|
|
|
|
7! |
|
|
|
|
|||||||||||||||||
9

æ |
|
z2 |
|
z4 |
|
z6 |
ö |
æ |
z3 |
|
z5 |
|
z7 |
ö |
|
= ç1 |
- |
|
+ |
|
- |
|
+ ...÷ |
+ i ×ç z - |
|
+ |
|
- |
|
+ ...÷. |
|
2! |
4! |
6! |
3! |
5! |
7! |
||||||||||
è |
|
|
|
ø |
è |
|
|
ø |
Порівнюючи ряди в дужках з рядами |
|
[5] і [4], дістаємо: |
|
|||||||||||||||||
|
|
|
ei×z |
= cos z + i ×sin z |
[7]. |
|
|
|
|
|
||||||||||
Аналогічно, підставляючи в ряд [6] |
|
замість z |
|
значення - i × z , дістанемо: |
||||||||||||||||
|
|
|
e-i×z |
|
= cos z - i ×sin z |
|
[8]. |
|
|
|
|
|
||||||||
Формули [7] і |
[8] називаються формулами Ейлера. Якщо почленно додати |
|||||||||||||||||||
(відняти) рівності [7] і |
[8], то матимемо іншу форму запису формул Ейлера: |
|||||||||||||||||||
cos z = |
ei×z |
+ e-i×z |
|
[9], |
|
|
|
sin z = |
|
ei×z |
- e-i×z |
|
[10]. |
|||||||
|
2 |
|
|
|
|
|
|
|
|
|
|
|
2i |
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
Оскільки |
ek×2π×i |
= cos(k × 2π )+ i ×sin(k × 2π ) =1, k Z , то: |
||||||||||||||||||
|
|
|
|
|
|
|
|
|
ω = ez = ez ×ek×2π×i = ez+k×2π×i . |
|||||||||||
Тобто, функція |
ez є періодичною з уявним періодом |
2π ×i . |
|
|||||||||||||||||
5) Натуральна логарифмічна функція ω = Lnz |
|
|
визначається як обернена |
|||||||||||||||||
до натуральної показникової функції |
|
ez . |
ez |
|
|
|
|
|
|
|
|
|||||||||
Ця функція є многозначною, оскільки функція |
– періодична. |
|||||||||||||||||||
Оскільки в показниковій формі: z = |
|
z |
|
×ei×arg z+k×2π×i , |
|
|
|
|||||||||||||
|
|
|
|
|
||||||||||||||||
|
|
|
|
|
то |
|
ω = Lnz = ln |
|
z |
|
+ i ×arg z + k × 2πi [11]. |
|||||||||
|
|
|
|
|
|
|
|
|||||||||||||
Значення Lnz при k = 0 називається головним значенням логарифмічної функції і позначається: ln z . Отже, за означенням: ln z = ln z + i ×arg z .
Приклад 2.2 |
Обчислити значення функції у вказаних точках: |
|
|
|
||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
а) w = Lnz , |
z0 = -1; |
|
б) |
w = ln z , |
|
z0 = e ×i. |
|
|
|
|||||||
↓. а) |
|
z0 |
|
=1, |
arg z0 = π ; |
Ln(z0 ) = ln1+ i ×π + k × 2πi = πi ×(2k +1) . ↑. |
|
|||||||||||||||||||
|
|
|
||||||||||||||||||||||||
↓. б) |
|
z0 |
|
= e , |
arg z0 |
= π ; |
ln(z0 ) = ln e + i × π =1+ π ×i . ↑. |
|
|
|
||||||||||||||||
|
|
|
|
|
||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
2 |
2 |
|
|
|
|
|
Приклад 2.3 |
Розв’язати рівняння: |
ez + i = 0 . |
|
|
|
|
|
|
||||||||||||||||||
↓. ez = -i, тому |
z = Ln(−i), тобто |
|
|
|
|
|
|
|
|
|
||||||||||||||||
ln |
|
- i |
|
+ i ×arg(-i) + 2πki = -πi |
+ 2πki. |
↑. |
Відп.: πi × (2k + 0,5), |
k Z . |
||||||||||||||||||
|
|
|||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
6) Гіперболічні функції комплексної змінної визначаються рівностями: |
|
|||||||||||||||||||||||
ω = shz = |
ez |
- e− z |
ω = chz = |
|
ez |
+ e− z |
|
|
ω = thz = |
|
shz |
; ω = cthz |
= |
chz |
|
|||||||||||
|
|
|
; |
|
|
|
|
; |
|
|
|
. |
||||||||||||||
|
2 |
|
|
|
2 |
|
|
chz |
shz |
|||||||||||||||||
|
|
|
|
|
|
|
|
shz |
chz |
|
|
|
|
|
|
|
|
|
|
|
||||||
Функції |
|
та |
мають період 2π ×i . |
|
|
|
|
|
|
|
||||||||||||||||
10
