
Лаб_електрика_№4_2010
.pdf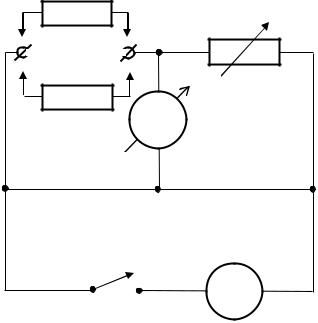
41
Rx = R0 |
R1 |
. |
(6.24) |
R |
|||
2 |
|
|
|
Таким чином, вибравши опори R1 і R2 , та змінюючи опірR0 , можемо визначити величину опору Rx .
2.24 Експериментальна установка
Схема експериментальної установки зображено на Рис. 2.24. Опори R1 і R2 є постійними опорами, величини яких вказані на установці. Клеми 1, 2 дають змогу вмикати в схему окремі невідомі опори Rx1 і Rx2 , а також опори Rx1 і Rx2 з'єднанні послідовно чи паралельно. З допомогою магазину опорів R0
здійснюють балансування мостової схеми, коли струм через гальванометр G дорівнює нулю.
Живлення схеми здійснюється від джерела U через вимикач SA.
RХ1
R0
1 |
2 |
RХ2
G
R1 |
|
R2 |
|
|
|
SA
U
Рис.2.24.
3.24 Хід виконання роботи
1.Включити джерело живлення.
2.Під'єднати до клем 1, 2 невідомий опір Rx1 , з допомогою вимикача SA подати
в схему струм і, змінюючи опір R0 , досягти балансу моста. Виміри повторити 5-7 разів ; результати занести у Таблицю 1.
3.Під'єднати до клем 1, 2 невідомий опір Rx2 , з допомогою вимикача SA подати в схему струм і, змінюючи опір R0 , досягти балансу моста. Виміри повторити 5-7 разів ; результати занести у Таблицю 1.
4.Під'єднати до клем 1, 2 опори Rx1 і Rx2 з'єднанні послідовно, з допомогою вимикача SA подати в схему струм і, змінюючи опір R0 , досягти балансу моста. Виміри повторити 5-7 разів ; результати занести у Таблицю 1.
42
5.Під'єднати до клем 1, 2 опори Rx1 і Rx2 з'єднанні паралельно, з допомогою вимикача SA подати в схему струм і, змінюючи опір R0 , досягти балансу моста. Виміри повторити 5-7 разів ; результати занести у Таблицю 1.
6.Зробити розрахунки опорів Rx1 , Rx2 , Rxпoс , Rxпaр за формулою (4.24) на основі отриманих експериментальних даних. Надійний інтервал похибки вимірювання ∆Rx розрахувати за формулою
∆Rx = |
R1 |
∆ |
|
|
(7.24) |
|
R0 . |
||||||
R |
||||||
|
2 |
|
|
|
|
|
7.Обчисленням показати, що одержані з вимірювання значення задовольняють у межах точності приладів такі відомі з теорії взаємозв'язки опорів:
Rxпoс = Rx1 + Rx2 , |
1 |
= |
1 |
+ |
1 |
. |
(8.24) |
Rxпaр |
|
|
|||||
|
|
Rx1 |
Rx2 |
|
|||
Для розрахунків можна застосувати програмні системи Excel, Мсad, ORIGIN та інші.
Використання Мсad: Приклад використання Мсad для розрахунків наведений в методичному посібнику [6.24].
Таблиця 1.
№ п/п R0, Ом
Rx1 |
Rx2 |
Rxпoс |
Rxпaр |
1
2
3
4
5
6
7
4.24 Контрольні запитання
1.24 Яка фізична величина називається опором провідника? В яких одиницях вона вимірюється?
2.24 У чому полягають закони Ома в інтегральній і диференціальній формах для ділянки кола? для замкнутого кола?
3.24 У чому полягають правила Кірхгова? Застосування правил Кірхгофа для розрахунку складних електричних кіл.
4.24 Виведіть формулу (4.24).
5.24 Застосовуючи правила Кірхгофа, виведіть формулу залежності різниці потенціалів між точками СД (рис. 1) від величини опорів R0 , R1 , R2 , Rx і
спаду напруги на ділянці АВ.
6.24 Намалюйте мостову схему і виведіть рівняння (5.24).
7.24 Виведіть формулу для розрахунку опору двох послідовно з’єднаних провідників
43
8.24 Виведіть формулу для розрахунку опору двох паралельно з’єднаних провідників
5.24 Література
1.24. Кучерук І.М., Горбачук І.Т.. Загальна фізика. Електрика та магнетизм.- К.: Вища школа. 1990.
2.24. Детлаф А.А., Яворский Б.М., Милковская Л.Б..Курс общей физики.
Т.1.2.3. - М.: Высшая школа, 1987.
3.24. Трофимова Т.И. Курс физики.М.:1983. 4.24. Савельев И.Н. Курс физики. Т 1-3.М.:1982.
5.24. Клименко А.П. та інш. Методичні вказівки №№1-9 до лабораторних рабіт.
6.24.Потапов А.О., Мотіна А.І. Методичні вказівки по використанню MCAD для опрацювання результатів лабораторних робіт фізпрактикума. К.:КНУТД. -2005.112с.
ЛАБОРАТОРНА РОБОТА № 26. ВИЗНАЧЕННЯ ВНУТРІШНЬОГО ОПОРУ ДЖЕРЕЛА СТРУМУ МЕТОДОМ «НЕСПРАВЖНЬОГО НУЛЯ»
Мета роботи: навчитись вимірювати внутрішній опір джерела за допомогою мостової схеми.
1.26 Теоретичні відомості
Для визначення внутрішнього опору джерела струму використовують два основні методи. Перший метод ґрунтується на законі Ома для замкнутого кола. Але точніші результати можна отримати при вимірюванні внутрішнього опору джерела струму методом «несправжнього нуля». Вимірювальна схема, яка є своєрідним мостом Уітстона, зображена на рис.1.26. Джерелом живлення моста
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
ε є те саме джерело, опір якого r |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
потрібно визначити. |
|
|
|
|
|
|
ε |
|
|
|
|
|
|
|
|
|
|
|
|
||
- |
|
+ |
|
|
|
|
|
R0 |
|
|
|
Джерело живлення розміщене в |
||||||||
|
r |
|
В |
|
|
|
|
|
||||||||||||
|
І |
|
|
|
|
|
|
|
|
|
|
|
|
І0 |
плечі АВ мосту. Опір діагоналі АС, яку |
|||||
|
|
|
|
|
|
|||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
можна закоротити вимикачем SA, |
|
|
І1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
G |
|
|||||||
|
|
|
|
|
|
|
|
ІП |
|
|
позначимо Rx . Міст складається також з |
|||||||||
|
|
|
|
|
|
|
|
|
І1 |
|
RП |
|
опору R0 , який є магазином опорів і |
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
А |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
С постійних відомих за величиною опорів |
||
|
|
R1 |
|
|
|
|
|
|
|
|
|
R2 |
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
R1 і R2 . Вимірювання внутрішнього |
|||
|
|
|
|
|
|
|
|
|
|
D |
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
І1 |
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
І2 |
|
опору джерела струму ґрунтується на |
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
SA |
|
тому, що змінюють опір R0 до того |
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
|
|
|
|
|
|
|
|
|
Рис.1.26. |
|
моменту, доки струм в діагоналі ВD |
|||||||||
|
|
|
|
|
|
|
|
|
|
перестане змінюватись при замиканні і |
||||||||||
перестане залежати від опору Rx |
|
розмиканні вимикача SA, тобто |
||||||||||||||||||
(«несправжній нуль»). |
||||||||||||||||||||
|
|
|
|
44 |
Знайдемо умову, за якої існує «несправжній нуль». Припустимо, що |
||||
струми на різних ділянках кола мають напрями, як це показано на рис.1.26. |
||||
Рівняння для контурів АВDА і ВСDВ даного кола запишуться |
||||
|
I r + Iп Rп + I1 R1 =ε , |
(1.26) |
||
|
I0 R0 − I2 R2 − I П RП = 0 , |
(2.26) |
||
а для вузлів В і D |
= 0 , |
(3.26) |
||
|
I − I П − I0 |
|||
|
I П − I1 − I2 |
= 0 . |
(4.26) |
|
При зміні опору Rx , наприклад, при замиканні вимикача SA, струми |
||||
приймуть нові значення: I +∆I , I1 +∆I1 , |
I2 +∆I2 і I0 +∆I0 . Струм I П в діагоналі |
|||
ВD за умовою не повинен змінюватись, тобто ∆IП = 0 . |
||||
Записавши рівняння Кірхгофа для кола, яке розглядається, з врахуванням |
||||
нових значень струмів у вигляді (1.26)-(4.26) і розглянувши спільно ці рівняння, |
||||
отримаємо |
|
|
|
|
|
∆I r +∆I1 R1 = 0 , |
|
||
|
∆I0 R0 −∆I2 R2 = 0 , |
|
||
або |
∆I = ∆I0 , ∆I1 = ∆I2 ; |
|
||
r ∆I = −R1 ∆I1 , |
|
|||
|
|
|||
|
R0 ∆I = −R2 ∆I2 . |
|
||
Таким чином |
|
|
|
|
|
r = R0 RR1 . |
|
(5.26) |
|
|
|
2 |
|
|
2.26 Експериментальна установка |
|
|||
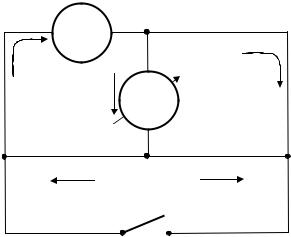
Схема експериментальної установки зображений на рис.2.26. Вона |
||||
включає джерело постійного струму U , постійні опориR1 і R2 , змінний опір R0 , |
||||
мікроамперметр А. Діагональ мостової схеми закорочується за допомогою |
||||
|
|
|
|
вимикача SA. |
- |
U |
+ |
R0 |
3.26 Хід виконання лабораторної |
|
r |
|
роботи |
|
|
|
|
||
|
|
|
|
1. Включити живлення джерела |
|
|
А |
струму U. |
|
|
|
2. Змінюючи опір R0 , добитись |
||
|
|
RП |
||
|
|
|
|
такого його значення, за якого |
|
R1 |
|
R2 |
замикання або розмикання вимикача |
|
|
SA не буде змінювати струм, який |
||
|
|
|
|
|
|
|
|
|
проходить через мікроамперметр А |
|
|
SA |
|
(«несправжній нуль»). |
|
|
Рис.2.26. |
|
|
45
3.Виміри повторити 5-7 разів і результати занести у Таблицю 1.26.
4.На основі отриманих експериментальних даних за формулою (5.26) зробити розрахунок величини внутрішнього опору r . Довірчий інтервал похибки вимірювання визначити за формулою
|
∆r = |
R1 |
∆ |
|
|
|
|
|
|
R0 . |
|||||||
|
|
|||||||
|
|
R |
||||||
|
2 |
|
|
|
|
|
Таблиця 1.26 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
№ п/п |
R0, Ом |
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
3 |
|
|
|
|
|
|
|
|
4 |
|
|
|
|
|
|
|
|
5 |
|
|
|
|
|
|
|
|
6 |
|
|
4.26 |
Контрольні запитання |
7 |
|
|
||||
|
|
|
||||||
1.26 |
Що являє собою електричний струм? За яких умов він виникає? |
|||||||
2.26 |
Що називається електрорушійною силою джерела? |
|||||||
3.26 |
Поясніть фізичний зміст електрорушійної сили, напруги і різниці |
|||||||
потенціалів? |
||||||||
4.26 |
За якої умови різниця потенціалів на полюсах джерела буде |
|||||||
максимальною? |
||||||||
5.26 |
За рахунок чого в замкнутому контурі буде виконуватись робота з |
|||||||
переміщення заряду по всьому колу? |
||||||||
6.26 |
Виведіть формулу (5.26). |
|||||||
5.26 Література
1.26. Кучерук І.М., Горбачук І.Т. Загальна фізика. Електрика та магнетизм.- К.: Вища школа. 1990.
2.26. Детлаф А.А., Яворский Б.М., Милковская Л.Б..Курс общей физики.
Т.1.2.3. - М.: Высшая школа, 1987.
3.26. Трофимова Т.И. Курс физики.М.:1983.
4.26.Савельев И.Н. Курс физики. Т 1-3.М.:1982.
5.26.Клименко А.П. та інші. Методичні вказівки №№1-9 до лабораторних рабіт.
ЛАБОРАТОРНА РОБОТА № 27. ГРАДУЮВАННЯ ТЕРМОПАРИ І ВИМІРЮВАННЯ КОЕФІЦІЄНТУ ТЕРМОЕЛЕКТРОРУШІЙНОЇ СИЛИ
Мета роботи: експериментально вивчити явище термоелектрорушійної сили, навчитися вимірювати коефіцієнт термоелектрорушійної сили термопари.
46
1.27Теоретичні відомості
У1877 році А. Вольта зробив відкриття: коли два різних метали приходять у взаємний контакт, між ними виникає різниця потенціалів. Ним був встановлений ряд металів, в якому кожний попередній метал у контакті з одним із наступних електризується позитивно. Цей ряд має вигляд: Al , Zn , Cd , Pb ,
Sb , Bi , Hg , Fe , Cu , Ag .
При подальшому дослідженні було встановлено, що якщо кілька різних металів приєднати один до одного послідовно, то на кінцях кола виникне різниця потенціалів, яка залежить від природи крайніх провідників і не залежить від того, які провідники знаходяться між ними. Різниця потенціалів, яка виникає при зіткненні різнорідних металів, була названа контактною різницею потенціалів. Контактна різниця потенціалів зумовлена неоднаковими роботами виходу електронів з контактуючих металів і неоднаковою концентрацією електронів.
В металах або їх сплавах структурні частинки (атоми чи молекули) розташовуються у вузлах кристалічних грат, зближуючись так, що орбіталі - електронні оболонки, зовнішніх валентних електронів перекриваються. Через це валентні електрони належатимуть усім структурним частинкам у межах об′єму кристала тому, що не можна позначити їх належність до якогось певного атому. Це означає, що валентні електрони в межах металу створюють спільність подібно газу вільних електронів, у який занурено кристалічні грата з іонами у вузлах.
Вузли кристалічної решітки металу (додатні іони) знаходиться у постійному тепловому коливальному русі, а вільні електрони - у хаотичному тепловому русі, маючи теплову кінетичну енергію величиною kT. Електронний газ утримується к металі силами електричної взаємодії з іонами кристалічних грат – тобто являють собою частинки, які знаходяться в потенційному полі, через що їх розподіл по енергіях можна вважати Больцманівським. Величину електричної взаємодії електронів з іонами кристалічних грат характеризуватимемо «роботою виходу» А, тобто величиною роботи, яку мають виконати зовнішні сили, аби електрон міг би вийти з металу.
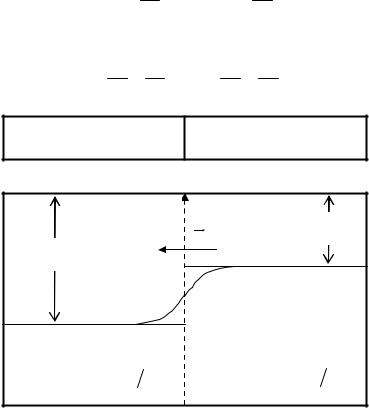
Примемо, умовно, що робота виходу A1 металу M1 (Рис.1.27.) більша від роботи виходу A2 металу M 2 ( A1 > A2 ), а концентрація електронів n1 < n2 . Тоді, коли метали приходять у взаємний контакт, деяка частина електронів починає дифундувати з металу M 2 в метал M1 , внаслідок чого останній метал M1 , заряджається негативно, а перший M 2 - позитивно. На контакті виникає внутрішнє електричне поле з напруженістю Е , яке буде протидіяти подальшій дифузії електронів з металу M 2 в метал M1 . Через деякий час – час релаксації, встановиться динамічна рівновага, для якої буде характерний розподіл концентрації електронів в металах, що показаний штрих-пунктирною лінією на Рис. 1.27.
Кожному значенню роботи виходу можна спів ставити певний потенціал
47
A1 =e ϕ1 , A2 =e ϕ2 .
Для концентрації електронів у потенціальному електричному полі з відповідним потенціалом на контакті двох металів можна записати у вигляді
|
|
|
|
−eϕ1 |
|
|
|
−eϕ2 |
|
|
n |
1 |
= n e |
kT , n |
2 |
= n |
02 |
e kT . |
|
|
|
01 |
|
|
|
|
|||
Звідки можна одержати, вважаючи n01 ≈ n02 |
|
||||||||
|
ϕ1 |
= − kT ln n1 , ϕ2 |
= − kT ln n2 . |
|
|||||
|
|
|
e |
n |
|
|
e |
n |
|
|
|
|
|
01 |
|
|
|
02 |
|
|
|
|
М1 |
|
|
|
|
М2 |
|
|
|
|
|
W |
|
|
|
|
А2 |
|
|
|
|
|
|
E |
|
|
|
|
А1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
n1 |
= n01 exp( − A1 |
kT ) |
|
n2 = n02 exp( − A2 |
kT ) |
||||
|
|
|
Рис.1.27. |
|
|
|
|
|
|
Між вільними кінцями з'єднаних металів вбуде діяти різниця потенціалів - «контактна різниця» потенціалів.
ϕ2 −ϕ1 = |
A2 − A1 |
+ kT |
ln |
n2 |
. |
(1.27) |
e |
|
|||||
|
e |
|
n1 |
|
||
Неважко перевірити, що в замкнутому колі, при деякій температурі T контактна різниця потенціалів дорівнює нулю. Інша справа, коли один із спаїв підтримувати при температурі T1 , а другий - при температурі T2 . У такому разі в
замкненому колі з'явиться контактна різниця потенціалів, яка збуджує в ньому електричний струм. Цю різницю потенціалів називають термоелектрорушійною силою:
ε = |
k(T1 −T2 ) |
|
ln |
n2 |
=α (T1 −T2 )=α ∆T , |
(2.27) |
|
e |
n1 |
||||||
|
|
|
|
||||
де k - стала Больцмана, e - заряд електрона, α - коефіцієнт термоелектрорушійної сили.
Експеримент показує, що α різних пар металів і даної пари металів для різних температурних інтервалів має неоднакове значення. Тому для практичної роботи слід знати диференційні значення α при різних температурах:

48
α = |
dε |
≈ |
∆ε |
, |
(3.27) |
|
dT |
∆T |
|||||
|
|
|
|
на основі яких складається градуювальник графік термопари. Термопара являє собою прилад, що складається з двох різнорідних
металевих провідників (дротин), що мають надійний контакт (кінці їх спаяні). Термопари широко використовуються для вимірювання температури, зокрема мідь-константановими, або залізо-константановими термопарами вимірюють температури до 500-800 ºС, а платиновими з домішками родію (платинаплатина плюс 10% родію) температури до 1700 ºС.
2.27Експериментальна установка
Вданій роботі необхідно проградуювати (тобто встановити залежність термоелектрорушійної сили від різниці температури спаїв) термопару константан-мідь і визначити коефіцієнт термоелектрорушійної сили.
Схема і фото експериментальної установки приведені на Рис.2.27.
Рис.2.27.
Установка включає дві термопари, одна з яких розташована в масляній ванні і може підігріватись електричним нагрівачем, друга - розташована в масляній ванні і знаходиться на відкритому повітрі. Температура кожної термопари контролюється ртутними термометрами Т і Т0 відповідно. Між собою термопари з'єднані провідниками з однакових металів, інші вільні кінці термопар підключені до вхідних клем цифрового вольтметру.
3.27 Послідовність виконання лабораторної роботи
1.Підключити до електричної мережі цифровий вольтметр і увімкнути його. За
допомогою термометрів Т і Т0 виміряти і записати величини температур «холодного» - того що в повітрі, і «гарячого» - того що контактує з нагрівачем, спаїв.
2.Ввімкнути нагрівач. При підвищенні температури від початкової до 60 ºС вимірювати термоелектрорушійну силу через кожні 5 ºС. Результати вимірів занести в Таблицю 1.
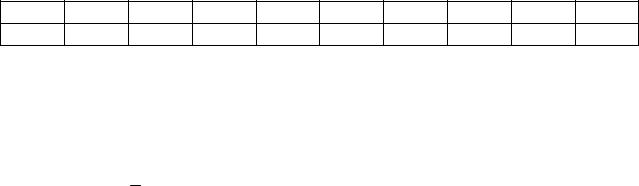
3.Побудувати графік залежності ε = f (∆T ). Припустивши, що термоелектрорушійна сила термопари лінійно залежить від різниці
49
температур між спаями визначити коефіцієнт термоелектрорушійної сили
α = ∆ε ∆T .
∆T .
Таблиця 1
∆T, °C
ε, мВ
4.27 Опрацювання результатів вимірювання.
Прийнявши, що термоелектрорушійна сила термопари лінійно залежить від температури (2.27), покладемо y лінійній залежності y=a+bx
y = ε, x = ∆T, b =α .
Методом найменших квадратів визначити коефіцієнт термоелектрорушійної сили α та його довірчий інтервал. Результат записати у вигляді
α =α ± ∆α, P = 0,95 .
Для розрахунків можна застосувати програмні системи Excel, Мсad, ORIGIN та інші.
Використання Мсad: Приклад використання Мсad для розрахунків наведений в методичному посібнику [6.27].
5.27Контрольні запитання
1.27Що називається роботою виходу електрона з металу і від чого вона залежить?
2.27 Сформулюйте закони Вольта і на основі електронної теорії виведіть формулу для визначення контактної різниці потенціалів між двома металами.
3.27Що називається термоелектрорушійною силою і від чого вона залежить?
4.27Доведіть, що контактна різниця потенціалів залежить від температури.
5.27Що являє собою термопара і для чого вона використовується?
6.27Які переваги має термопара в порівнянні з спиртовим і ртутним термометрами?
6.23Література
1.27. Кучерук І.М., Горбачук І.Т.. Загальна фізика. Електрика та магнетизм.- К.: Вища школа. 1990.
2.27. Детлаф А.А., Яворский Б.М., Милковская Л.Б..Курс общей физики.
Т.1.2.3. - М.: Высшая школа, 1987.
3.27. Трофимова Т.И. Курс физики.М.:1983. 4.27. Савельев И.Н. Курс физики. Т 1-3.М.:1982.
5.27. Клименко А.П. та інш. Методичні вказівки №№1-9 до лабораторних рабіт.
6.27.Потапов А.О., Мотіна А.І. Методичні вказівки по використанню MCAD для опрацювання результатів лабораторних робіт фізпрактикума. К.:КНУТД. -2005.112с.

50
ЛАБОРАТОРНА РОБОТА № 28. ДОСЛІДЖЕННЯ ВОЛЬТ-АМПЕРНИХ ХАРАКТЕРИСТИК ВАКУУМНОГО ТРІОДА І ВИЗНАЧЕННЯ ЙОГО ПАРАМЕТРІВ
Мета роботи: вивчити вольт-амперні характеристики вакуумного тріоду і навчитись розраховувати його параметри.
1.28 Теоретичні відомості
Тріод -це електронна лампа, яка має три електроди. Джерелом електронів, як і в усіх лампах, служить катод - електрод, який нагрівається до високої температури (600-І200°С). В найпростішому випадку катод роблять у вигляді металевого провідника, який розжарюється струмом. Електрони, що залишили катод в наслідок термоелектронної емісії, прямують до електрода лампи, який називається анодом, - на нього подають позитивний потенціал відносно катода. Густина струму емісії jН при його насичені (коли всі емітовані електрони досягають аноду) визначається за законом Річардсона-Дешмена
jH = B T 2 exp(− A kT ) , |
(1.28) |
де: В –стала, Т- температура катоду, А – робота виходу електронів з матеріалу катоду, k – стала Больцмана.
Для управління електронним потоком в тріоді є електрод, який називається сіткою. Звичайно вона являє собою тонкий провідник, який намотують на спеціальний тримач так, щоб сітка охоплювала катод. Якщо змінювати потенціал сітки, то буде змінюватись кількість електронів, які попадають з катода на анод.
Характеристиками тріода є: залежність анодного струму Іа від температури катоду Т при постійній анодній Uа і сітковій Uс напругах ; залежність анодного струму Іа від анодної напруги Uа при постійних Т і Uс (анодна характеристика), залежність анодного струму Іа від напруги на сітці Uс (сіткова характеристика) при постійних Т та Uа.
Залежність анодного струму Іа від анодної напруги Uа підкоряється
закону Ленгмюра-Богуславського |
(2.28) |
Ia =α Ua3 2 , |
де: α - стала.
Найбільш важлива характеристика - сіткова характеристика, тому що звичайно в умовах роботи тріода змінною величиною є напруга на сітці. Знаючи дві сіткові характеристики, отримані для двох різних анодних напругах Uа1 і Uа2_, можна визначити основні параметри лампи, якими є крутість сіткової характеристики S , внутрішній опір Rі та коефіцієнт підсилення µ.
3 метою визначення параметрів лампи по трьох точках, взятих на прямолінійній ділянці сіткових характеристик, нанесених на одному графіку (рис. 28.1), будується характеристичний прямокутний трикутник. Одна сторона цього трикутника ВС визначає зміну напруги на сітці ∆Uс, а друга АВ - зміну анодного струму ∆Ιа. Визначивши значення ВС = ∆Uс у вольтах і АВ = ∆Ιа у
