Лаб_електрика_№4_2010

21

2.Контакти в місцях з’єднання провідників повинні бути надійними.

3.Переплетіння навіть ізольованих провідників не допускається.

4.Джерело струму потрібно підключати в останню чергу, а відключати в першу чергу.

5.Усі реостати, що вмикаються в коло, попередньо повинні бути встановлені на максимальний опір.

6.потенціометри попередньо встановлюються на мінімум напруги, що подається в коло.

7.Усі ключі та комутатори перед виконанням роботи повинні бути розімкнені.

8.Приступати до виконання роботи без перевірки схеми викладачем чи черговим лаборантом забороняється.

9.Електричне коло замикається тільки на час виконання вимірювань і запису

показань приладів.

При виконанні лабораторних робіт забороняється:

-Вмикати рубильники та вилки без дозволу викладача або чергового лаборанта.

-Перемонтовувати схему, яка знаходиться під напругою.

-Торкатися неізольованих ділянок схеми.

-Залишати без нагляду схему, яка знаходиться під напругою.

ЛАБОРАТОРНА РОБОТА № 1-II. ВИМІРЮВАННЯ ПИТОМОГО ОПОРУ ПРОВІДНИКА

Мета роботи:

1.Вивчити принципи роботи електровимірювальних приладів і застосування їх для вимірювання напруги U та струму I.

2.Виміряти величину опору Rx ділянки електричного кола, застосовуючи вольтметр та амперметр.

1.1-II Теоретичні відомості

Питомий опір провідника можна було б виміряти, якщо виготовити з даного матеріалу провідник довжиною один метр з площею поперечного перерізу рівною одному квадратному метру і виміряти його опір. Питомий опір провідника є фізичною характеристикою матеріалу і його стану, яка однакова для провідників різної форми виготовлених з однакових матеріалів. Опір провідника правильної геометричної форми R можна розрахувати знаючи його питомий опір ρ , довжину l і площу поперечного перетину S :

Найпростішим способом вимірювання опору є метод амперметра і вольтметра. Він зводиться до того, що до провідника прикладають напругу, яка вимірюється вольтметром, і амперметром вимірюють струм, який проходить через провідник. Далі користуючись законом Ома можна розрахувати опір провідника.

22

Струм в провіднику – це направлений рух електронів провідності, які виникають при усуспільненні валентних електронів атомів металу. Згідно класичних уявлень ці електрони представляють собою газ, що має три ступені свободи. При кімнатній температурі швидкість руху електронів провідності - ≈103 м/с, а довжина вільного пробігу – всього 10−10 м. При максимально допустимих величинах струму швидкість направленого руху становить всього 10−3 м/с, що в 106 менше за швидкість теплового руху.

В межах класичних уявлень електричний опір обумовлений зіткненням електронів провідності з вузлами кристалічної решітки і її дефектами, куди входять порушення періодичності решітки, атоми металу, розміщені між вузлами решітки, відсутність атома в вузлі решітки, різні домішки. Тому, за рідкими винятками, опір сплаву металі більший за опір його складових.

2.1-II. Експериментальна установка і порядок проведення вимірювань.

Зовнішній вигляд лабораторної установки показаний на рис. 1.1-II Уздовж стійки з поділками натягнуто дротяний провідник (реохорд). Уздовж провідника можна пересувати контактний затискач і, таким чином, включати в схему вимірів частину провідника, розташовану між точками А і С. У вимірювальному блоці знаходяться джерело постійної напруги з регулятором струму і вимірювальні прилади – амперметр і вольтметр. Для виміру опору між точками А і С використовується метод амперметра і вольтметра, при цьому за допомогою перемикача можна вибирати дві різні схеми підключення приладів до вимірюваного опору. Тут використовуватимемо схему показану на рис. 2.1-II (Uo- напруга джерела, rа, rв - внутрішні опори амперметра і вольтметра). На тому ж рисунку показана відповідна еквівалентна схема.

У схемі вольтметр показує напругу на паралельному з'єднанні вимірюваного опору і вольтметра, тому

Відповідно до методу амперметра-вольтметра і закону Ома вимірювана величина опору буде рівна

Користуючись формулою (1.1-II) знаходимо дійсні значення шуканого опору:

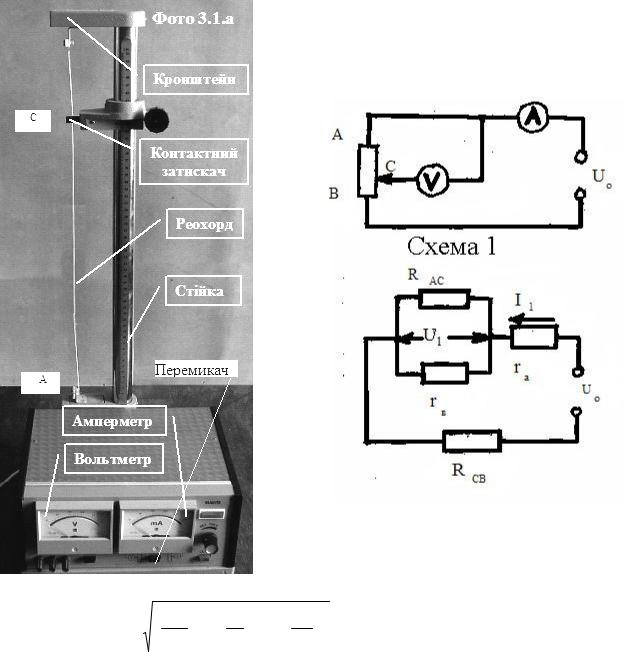
Якщо l - довжина провідника, (див. рис. 1-II.1), S = π d 2 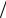4 - площа його поперечного перетину, яка розраховується з виміряного діаметру дроту d , то для питомого опору металу отримаємо:

23

де R1 - величина опору порахована по формулі (3.1-II).

3.1-II Хід виконання роботи

1.Перевести ручку регулятора струму в крайнє ліве положення. Ковзаючий контакт встановити в середнє положення. Перемикач встановити в натиснене положення, що відповідає схемі 1.

2.Для вибраної довжини дроту зробити виміри l і d, результати занести до таблиці 1.1-II.

3.Включити установку в мережу (виконує лаборант). Регулятором струму

встановити величину струму I1 = 150 мА, зробити виміри напруги U1 і струму I1 в схемі 1. Отримані дані занести до таблиці 1.1-II.

4.Зробити обробку результатів прямих вимірювань, представлених в таблиці

1.1-II.

Таблиця 1.1-II.

l, м

∆l, м

d, м

∆d, м

U, В

∆U, В

I, А

∆I, А

R1, Ом

∆R1

ρ, Ом·м

∆ρ, Ом·м

5.Виходячи з характеристик електровимірювальних приладів порахувати абсолютні похибки вимірювання величини струму ∆ I1 і напруга ∆U1:

∆x = k Xг

де: k – клас точності приладу у відносних одиницях, Хг – верхня межа вимірювань приладу.

6.По формулі (2.1-II) розрахувати величину R1.

7.Розрахувати абсолютну похибку вимірювання R1 :

8.По формулі (1-II-2.4) розрахувати величину ρ.

9.Розрахувати абсолютну похибку вимірювання питомого опору ρ:

24

10. Результати записати до таблиці 1-II-1.

4.1-II Контрольні питання

1.1-II Сформулюйте закон Ома для однорідного металевого провідника. Поясніть, від яких параметрів залежить його електричний опір.

2.1-II Яким чином з результатів вимірів визначається величина питомого опору провідника?

3.1-II Порядок обробки результатів вимірів і розрахунку похибок.

5.1-II Література

1.1-II Кучерук І.М., Горбачук І.Т., Луцик П.П. Загальний курс фізики: Навчальний посібник – Т. 2.: Електрика і магнетизм. – К.: Техніка, 2001. – 452 с.

2.1-II Савельев И.В. Курс общей физики. Т. 2. М.: Наука, 1998 г.

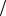
26

і через опір шунта. Оскільки вони включені паралельно, спад напруги на них буде однаковий UΠ . Величина RШ визначається із співвідношення

амперметра: вольтметр включають паралельно опору ділянки кола, амперметр послідовно в коло.

За такої схеми вимірювання покази вольтметра відповідають U , але покази амперметра I0 збільшуються на величину IB , тобто на величину струму,

який протікає через вольтметр. Це методична похибка систематичного характеру. Для її мінімізації необхідно ввести поправку - відняти з показів амперметра I0 величину IB : I = I0 − IB .

В якості вольтметру і амперметру можна використовувати мікроамперметри — один з додатковим опором, другий з шунтом (Рис. 1.21 та Рис. 2.21).

2.21 Експериментальні дослідження

Схема експериментальної установки для дослідження вольтметра і амперметра та визначення опору ділянки електричного кола приведена на (Рис. 3.21). Експериментальна установка включає джерело живлення Е, яке підключається до вимірювального кола ключем К. Напруга на ділянці кола змінюється за допомогою реостата R0 . Опір ділянки кола встановлюється

величиною RX 1 або RX 2 за допомогою перемикача П. Сила струму через ділянку кола вимірюється амперметром, який складається з мікроамперметра ІПА і шунта RШ . Падіння напруги на ділянці кола вимірюється вольтметром, який складається з мікроамперметра ІПВ і додаткового опору RД.

В якості додаткового опору і шунта використовують відповідні магазини опорів.

Величини додаткового опору RД і шунта RШ розраховуються перед виконанням вимірів, використовуючи відповідні параметри мікроамперметрів, а саме: максимальне значення струмів ІПА , ІПВ та величини внутрішніх опорів RПА і RПВ , які позначені на шкалах приладів.

Надійний інтервал похибки визначення ∆R з закону (3.21) при одноразовому вимірюванні можна обчислити за формулою

27

де ∆I і ∆U — відповідно абсолютні похибки вимірювання струму і напруги, які визначаються виходячи з класу точності відповідних приладів.

3.21Хід виконання лабораторної роботи

1.Вивчити принцип дії електровимірювальних приладів.

2.Задавши U Н = 2 В і IН = 2 мА, розрахувати за формулами (1.21), (2.21) додатковий опір RД і шунт RШ . Значення IП і RП приведені на шкалах відповідних приладів. округлити отримані значення до значущих цифр.

3.Встановити розраховані значення опорів на відповідних магазинах опорів.

4.Встановити повзунок дільника R0 в ліве положення (обертати проти годинникової стрілки).

5.Встановити опір ділянки кола RX 1 перемикачем П і включити живлення ключем К (положення ВКЛ,)

6. Змінюючи положення повзунок дільника R0 визначити покази приладів IB і IA для 8-10 пар значень . Виміряні величини IB і IA занести до таблиці 1.21.

7.Згідно з розширеними межами вимірювання U Н = 2 В і IН = 2 мА перерахувати виміряні значення IB і I A у величини U і I . Занести отримані значення до таблиці вимірів (Таблиця 1.21).

8.Виконати вимірювання за п.п.5-7 для опору ділянки кола RX 2 . Таблиця 1.21.

28

9. Знайти найбільш імовірні значення опорів RX 1 та RX 2 і межі довірчих

інтервалів за допомогою методу найменших квадратів, використовуючи програмні продукти Ecxel, МСаd , ORIGIN.

10. Результати вимірювання для кожного з опорів записати у вигляді

R = R ± ∆R, P = 0,95 ,

де R середнє значення, ∆R границя довірчого інтервалу, Р довірча імовірність розрахунку.

4.21 Контрольні запитання

1.21 Які прилади називаються електровимірювальними? За якими ознаками вони поділяються на різні типи?

2.21 Як побудовані електровимірювальні прилади магнітоелектричної системи? Який принцип дії цих приладів?

3.21Яка будова і принцип дії приладів електромагнітної системи?

4.21Основні характеристики електровимірювальних приладів. За допомогою яких співвідношень вони визначаються?

5.21Яку величину називають класом точності приладу? Як за допомогою класу точності визначити абсолютну похибку вимірювання?

6.21 Яке призначення амперметру? Як амперметр вмикається в електричне коло? Який порядок величини внутрішнього опору амперметрів?

7.21 Яке призначення вольтметру? Як вольтметр вмикається в електричне коло? який порядок величини його внутрішнього опору?

8.21 Які величини називають коефіцієнтом шунтування і коефіцієнтом розширення меж вимірювання за допомогою вольтметру? Виведіть формули

(1.1-II) і (2.1-II).

9.21 Які позначення наносяться на шкалу електровимірювальних приладів? 10.21 Яку величину називають ціною поділки і як її визначають?

11.21 За якими формулами в даній роботі обчислюється величина невідомого опору і надійний (довірчий) інтервал похибки?

29

12.21 Сформулюйте закон Ома для замкненого електричного кола, однорідної і неоднорідної ділянок кола?

13.21 Що називається електричним опором провідника? Від чого залежить ця фізична величина? Які її одиниці вимірювання?

14.21 Що називається спадом напруги? Як визначається ця величина? Які її одиниці вимірювання?

5.21 Література

1.21 Кучерук І.М., Горбачук І.Т.. Загальна фізика. Електрика та магнетизм.- К.: Вища школа. 1990.

2.21Детлаф А.А., Яворский Б.М., Милковская Л.Б..Курс общей физики. Т.1.2.3.

-М.: Высшая школа, 1987.

3.21Трофимова Т.И. Курс физики.М.:1983.

4.21 Савельев И.Н. Курс физики. Т 1-3.М.:1982.

5.21 Клименко А.П. та інш. Методичні вказівки №№1-9 до лабораторних рабіт. 6.21 Потапов А.О., Мотіна А.І. Методичні вказівки по використанню MCAD для опрацювання результатів лабораторних робіт фізпрактикума. К.:КНУТД.

-2005. 112с.

ЛАБОРАТОРНА РОБОТА № 22. ВИВЧЕННЯ ЕЛЕКТРИЧНОГО ПОЛЯ

Мета роботи: вивчення однорідного електричного поля (поля плоского конденсатора); вивчення електростатичного поля двох точкових зарядів.

1.22 Теоретичні відомості

Оскільки електричні заряди взаємодіють через простір – безконтактно, то матеріальний носій (субстанцію) взаємодії в цьому просторі назвали силовим електричним полем. Тобто кожен електричний заряд створює навколо себе це електричне поле, за посередництвом якого він взаємодіє з іншими зарядами.

Іншими словами: простір де діють електричні сили це і є електричне силове поле. Силовою характеристикою кожної точки електричного поля є

напруженість E = Fq , яка визначається величиною сили F , що діє з боку поля на заряд q, котрий знаходиться в електричному полі.

Робота А по переміщенню одиничного точкового додатнього заряду q з однієї точки х1 електричного поля в другу х2 вздовж, скажемо, осі x за умови, що точки розміщені нескінченно близько одна до одної і x2 − x1 = dx , дорівнює

A = q Ex dx . Та ж робота чисельно дорівнює зміні енергії електричного поля А = -∆П, тому можна ввести енергетичну характеристику поля – потенціал, а

де символ частинної похідної підкреслює, що диференціювання відбувається тільки по x .

30

З фізичної точки зору вираз (1.22) означає знаходження величини зміни потенціалу (скалярної величини) по заданому (ох) напрямку. З математичної

одиничного вектора i та диференційного оператора.

Оскільки напруженість електричного поля – величина векторна, яка характеризує і величину сили взаємодії і її напрямок, для геометричної інтерпретації електричного поля вводиться поняття «силова лінія» електричного поля – лінія в просторі, вздовж якої (по дотичній) діє електрична сила (вектор напруженості електричного поля). Тобто вздовж «силової лінії» величина напруженості електричного поля є постійною.

Для графічного зображення розподілу потенціалу електростатичного поля користуються еквіпотенціальними поверхнями (лініями) - поверхнями, в усіх точках яких потенціал ϕ має однакове значення.

Якщо поле створюється точковим зарядом, його потенціал

ϕ = 4πε10ε Qr ,

де Q - точковий заряд; ε0 - електрична стала; ε - діелектрична проникність

середовища; r - відстань від заряду до розглядуваної точки.

Таким чином, еквіпотенціальні поверхні точкового заряду - концентричні сфери. З іншого боку силові лінії напруженості у випадку точкового заряду - радіальні прямі. Звідси випливає, що силові лінії напруженості поля перпендикулярні до еквіпотенціальних поверхонь. Аналогічний висновок випливає з властивостей векторного добутку (1.22).

Аналіз більш загальних випадків підтверджує те, що лінії напруженості завжди нормальні до еквіпотенціальних поверхонь. Еквіпотенціальних поверхонь навколо кожної системи зарядів можна провести безліч. Однак їх, як правило, проводять так, щоб різниця потенціалів між будь-якими двома сусідніми еквіпотенціальними поверхнями була однакова. В цьому випадку густина еквіпотенціальних поверхонь наглядно характеризує напруженість поля в різних точках.

Вивчення електростатичного поля, створеного системою електродів довільної форми, має велике значення для конструювання електронних ламп, електродів електронно-променевих трубок, фокусуючих систем електронних мікроскопів і т.п.

Розрахункові й експериментальні методи дослідження електростатичного поля, локалізованого між електродами складної форми, становить значні труднощі. Тому широко використовується моделювання електростатичного поля за допомогою електролітичних ванн, заповнених слабким розчином електроліту, в який занурені електроди досліджуваної форми. При підключенні електродів до джерела струму, в електроліті створюється розподіл потенціалу,