Лекція 9.1. Пряма лінія на площині.

1. Види рівнянь прямої.

1. Рівняння прямої, що проходить через дану точку перпендикулярно даному вектору

Нехай на площині ХО задана точка М₀(х₀,y₀) і вектор (A,B). Запишемо рівняння прямої, що проходить через М₀ перпендикулярно вектору .

Рівнянням прямої буде таке рівняння, якому задовольнять координати кожної точки, що лежить на цій прямій, і не задовольняють координати будь-якої точки, що не лежить на цій прямій. Для складання рівняння візьмемо точку М(х,y). Розглянемо вектор (x—x₀,y—y₀). Тоді для прямої необхідна умова

()=(x—x₀)A+(y—y₀)B=0. (9.1)

Це і є шукане рівняння.

2. Загальне рівняння прямої. Пряма як лінія першого порядку. Окремі випадки рівняння прямої.

З рівняння (9.1) одержимо, розкривши дужки

Ax+By—Ax₀—Bx₀=0  Ax+Bx+C=0. (9.2)

число

Рівняння (9.2) і є загальне рівняння прямої на площині.

Зауваження: Лінія, рівняння якої є рівняння першого степеня, називається лінією першого порядку.

Якщо дано рівняння першого степеня, то коефіцієнти при змінних х и y – це А і В, які є коефіцієнтами вектора , перпендикулярного цій прямій.

Приклад: 5х—7y+8=0, те (5,-7).

3. Рівняння прямої, що проходить через дану точку, паралельно даному вектору.

Нехай пряма проходить через дану точку М₀(х₀,y₀) паралельно даному вектору (m,n). Тоді

. (9.3)

Це умова паралельності векторів.

Приклад: М₀(5,7), =(-2,3) те рівняння прямої буде

3х+2y—29=0.

4. Рівняння прямої, що проходить через дві точки.

Тоді

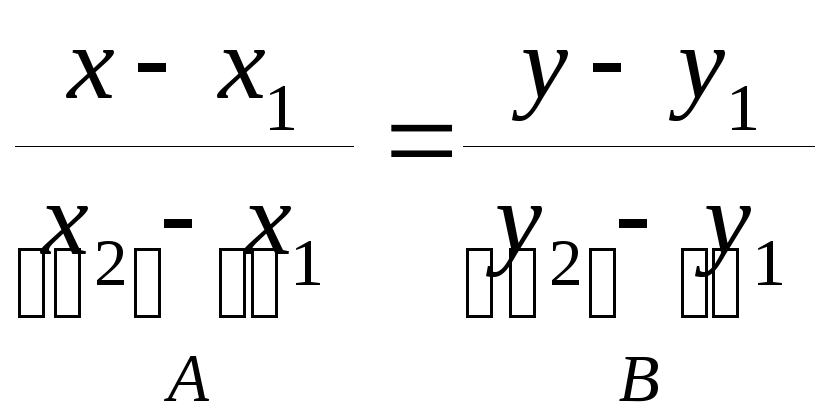. (9.4)

5. Параметричне рівняння прямих.

Нехай дане рівняння . Тоді

(9.5)

Це і є параметричне рівняння прямої, де t – параметр.

Приклад: М₀(5,7), =(-2,3).

6. Рівняння прямої з кутовим коефіцієнтом.

Нехай пряма задана рівнянням

, n0.

Помножимо на «n», одержимо

n/m(x—x₀)=y—y₀,

n/m — кутовий коефіцієнт, рівний k,

k=tg,

де  — кут нахилу прямої до осі ОХ. Тоді

y—y₀= k(x—x₀). (9.6)

Це і є рівняння прямої, що проходить через дану точку в заданому напрямку. Тоді

kx—kx₀= y—y₀  y=kx+b,

де b=y₀—x₀.

7. Нормоване рівняння прямої.

Нехай на площині дана пряма, не перпендикулярна осям координат.

Позначимо через Р довжину перпендикуляра , — кут .

Знаючи Р и  напишемо рівняння цієї прямої, розглядаючи радіус вектор , тоді проекціянабуде

або ,

||=1, але₀=(cos,sin). Тоді можна записати

, (x,y)(cos,sin)=P,

xcos+ysin=P. (9.7)

Це і є нормоване рівняння прямої. A= cos, B= sin.

2. Відстань від точки до прямої на площині.

Задано пряму L, її рівняння Ах+Вy+С=0 і дана точка М₀(х₀,y₀). Необхідно знайти d — відстань від точки М₀ до прямої L. Проведемо через М₀ пряму перпендикулярну L й одержимо М₁(х₁,y₁)

.

Але х₁ й y₁ — невідомі. Тоді зробемо так, рівняння прямої NL і минаючої через М₀(х₀,y₀) може бути записане у вигляді

В(х-х₀)-А(y—y₀)=0.

Координати точки М₁(х₁,y₁), у якій перетинаються прямі L й N повинні задовольняти рівнянням обох цих прямих, тобто

(*)

До першого рівняння додамо й віднімемо Ах₀+Вy₀. Тоді

(**) А(х₁-х₀)+В(y₁—y₀)= —(Ах₀+Вy₀+С).

Для відшукання d піднесемо до квадрата другу з рівностей (*) і (**) і складемо почленно, одержимо

(A²+B²)[(x₁—x₀)²+(y₁—y₀)²]=(Ax₀+Bx₀+C)².

d²

Тоді

. (9.8)

Приклад: М₀(1,-4). Визначити її відстань до прямої 4х—3y+12=0.

.

Рівняння прямої у відрізках (самостійно).

Припустимо, що відомо координати точок перетину прямої з осями координат: а – з віссю ОХ, b – з віссю ОY (їх називають відрізками прямої на осях координат). Складемо за цим даними рівняння прямої. Тому що нам відомі М₁(а,0), М₂(0,b) через які проходить пряма, то можна написати рівняння

. (9.9)

Це рівняння називається рівнянням у відрізках. Його використовують тоді, коли за параметри, що визначають положення прямої на координатній площині зручно прийняти відрізки, що відтинають пряма на осях координат.

3. Кут між прямими.

Нехай дані дві прямі

А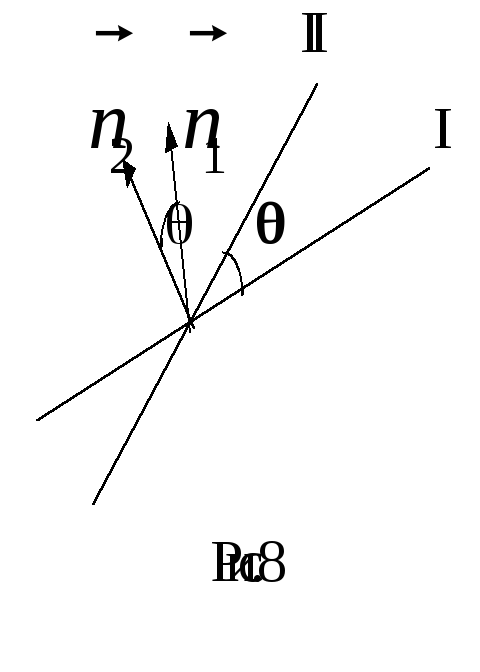₁х+В₁у+С₁=0

А₂х+В₂у+С₂=0

. (9.10)

Наприклад:

Зауваження: 1) Прямі перпендикулярні тоді й тільки тоді, коли cos=0, тобто А₁А₂+В₁B₂=0

=₂—₁,

. (9.11)

Якщо прямі паралельні, то tg=0, тобто k₂=k₁, а перпендикулярні, то 1+ k₁k₂=0, .

Лекція 9.3. Площина.

1. Види рівнянь площини.

1. Рівняння площини, що проходить через точку перпендикулярно даному вектору

Н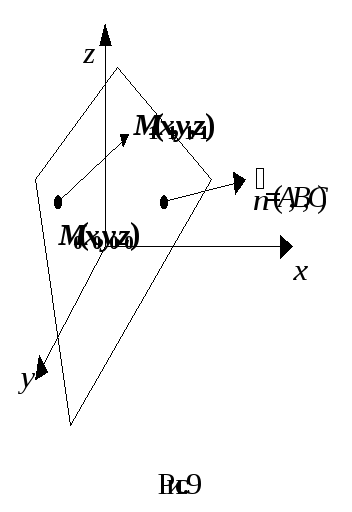ехай площина проходить через точку М₀(х₀,y₀,z₀) і перпендикулярна =(A,B,C).

Візьмемо на площині точку М(х,y,z), тоді .

A(x—x₀)+B(y—y₀)+C(z—z₀)=0. (9.12)

2. Загальне рівняння площини. Площина як поверхня першого порядку. Окремі випадки загального рівняння.

Перетворимо рівняння (13.13). Одержимо

Ax+By+Cz+D=0, (9.13)

де D= —(Ax₀+By₀+Cz₀)=const.

Це загальне рівняння площини, бачимо, що воно першого степеня відносно х, y, z.

Справедливо й зворотне твердження: усяке рівняння першого степеня відносно х, y, z є рівнянням площини.

Окремі випадки розглянути самостійно.

1. А=0  By+Cz+D=0 площина паралельна осі ОХ; В=0 || OY, С=0 || OZ.

2. D =0 — площина проходить через початок координат.

3. А=В=0  Cz+D=0— площина паралельна осям ОХ й ОY, тобто паралельна ХОY і перпендикулярна OZ  рівняння z=С.

А=C=0  ОY, В=C=0  ОХ й y=b, x=a.

4. А=D=0 — площина проходить через вісь ОХ, тобто вона паралельна ОХ і проходить через початок координат.

Аналогічно В=D=0 через ОY, C=D=0 через ОZ.

5. А=В=D=0 — площина збігається з ХОY рівняння z=0.

А=C=D=0  ХОY, y=0; C=В=D=0  YОZ, х=0.

3. Рівняння площини, що проходить через дану точку паралельно двом даним векторам.

М₀(х₀,y₀,z₀), =(a_x,a_y,a_z), =(b_x,b_y,b_z), М(х,y,z)

, ,— компланарні, тобто паралельні одній площини. Тоді ()=0, тобто

(9.14)

4. Рівняння площини, що проходить через три точки.

М₁(х₁,y₁,z₁), М₂(х₂,y₂,z₂), М₃(х₃,y₃,z₃)

=[(x₂—x₁),(y₂—y₁),(z₂—z₁)],

=[(x₃—x₁),(y₃—y₁),(z₃—z₁)],

. (9.15)

Приклад: Написати рівняння площини, що проходить через точки А(-2,3,1), В(-1,0,2), З(1,-2,3).

2. Відстань від точки до площини.

За аналогією з формулою знаходження відстані від точки до прямої на площині можна записати формулу знаходження відстані від точки до площини . Вона набирає вигляду

.

3. Кут між площинами.

Розглянемо дві площини  і , які задано відповідно рівняннями

,

.

Двогранний кут  між площинами  і  дорівнюватиме куту між векторами і , перпендикулярними до цих площин (рис.), тому

. (9.16)

Якщо площини взаємно перпендикулярні, то і дістанемо умову перпендикулярності двох площин:

. (9.17)

Якщо площини  і  паралельні між собою, то їхні вектори і — колінеарні, а отже, відповідні координати пропорційні, і ми маємо умову паралельності двох площин

. (9.18)

Лекція 9.5. Пряма лінія у просторі.

1. Види рівнянь прямої.

Пряму у просторі можна задати як лінію перетину двох площин у прямокутній системі координат:

(9.19)

Зрозуміло, що ці площини мають бути непаралельними, тобто їхні нормальні вектори , — не колінеарні. Система (9.19) називається загальним рівнянням прямої. Дістанемо ще деякі форми рівняння прямої.

Канонічне рівняння прямої. Нехай у системі координат Охуz задано пряму l і ненульовий вектор , колінеарний цій прямій. Точка належить прямій, а напрямний вектор . Тоді довільна точка М (х, у, z) лежатиме на прямій тоді і тільки тоді, коли вектори і колінеарні:

. (9.20)

Рівняння (9.20) називається канонічним рівнянням прямої у просторі.

Параметричне рівняння.

У рівнянні прямої (9.20) позначимо через t кожне з рівних відношень. Тоді

.

Звідси дістаємо:

Параметричне рівняння прямої в просторі.

Рівняння прямої, що проходить через дві задані точки.

Нехай дві точки і належать прямій у просторі. Тоді вектор можна розглядати як напрямний вектор прямої. Замінюючи ним вектор у рівнянні (9.20), дістанемо шукане рівняння прямої у просторі

.

Маючи кілька рівнянь однієї й тієї ж прямої, поміркуємо, як дістати зв’язок між ними. Розглянемо, як із загального рівняння (9.19) вивести канонічне рівняння (9.20). Для цього потрібно знайти точку, яка лежить на прямій, тобто розв’язати систему (9.19), і напрямний вектор прямої. Пригадуючи геометричний зміст коефіцієнтів у рівнянні площини, записуємо вектор — перпендикулярний до першої площини, а — неперпендикулярний до другої.

Рис.

Напрямний вектор прямої перпендикуляр­ний до обох цих векторів (рис.). Таким чином, . Використовуючи запис векторного добутку через визначник, дістаємо:

(9.21)

2. Кут між прямими у просторі.

і

візьмемо до уваги, що вектори і колінеарні відповідним прямим і скористаємося формулою:

.

З останньої формули випливає умова перпендикулярності двох прямих

,

а умову паралельності двох прямих дістанемо як умову колінеарності напрямних векторів і :

.

Розглянемо ще задачу знаходження відстані від точки до прямої .

Рис. 2.23

Шукану відстань можна розглянути як довжину висоти паралелограма, побудованого на векторах і (рис.). Відомо, що площа паралелограма дорівнює модулю векторного добутку векторів, на яких побудовано цей паралелограм. Доходимо висновку, що шукану висоту, а отже, і відстань від точки до прямої можна знайти за формулою:

(9.22)

Взаємне розміщення прямої і площини у просторі

Нехай задано пряму і площину у просторі. Якщо

,

то пряма перпендикулярна до площини, а коли

,

пряма паралельна площині.

Нехай . Знайдемо координати точки перетину площини і прямої. Перейдемо до канонічного рівняння прямої

і підставимо значення х, у, z у рівняння площини:

Звідси, використовуючи умову непаралельності, знайдемо значення параметра

.

Координати точки перетину:

.