1.6.5. Идеализированные цепи переменного тока

Цепь с активным сопротивлением R показана на рис. 1.13.

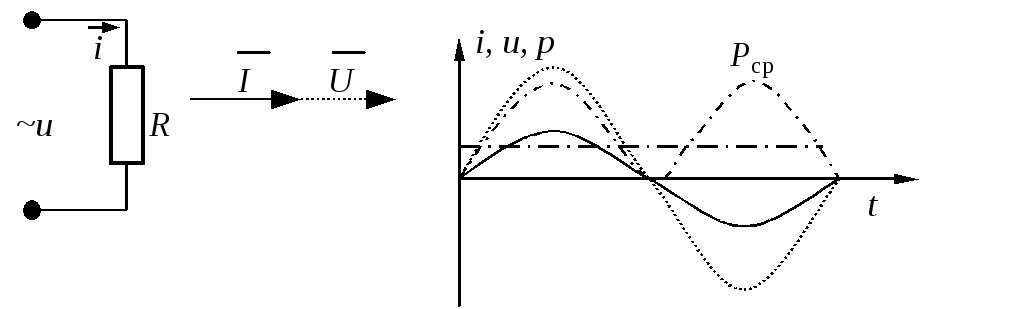
Рис. 1.13. Электрическая цепь с R (а), ее векторная диаграмма (б)

и графики (в) мгновенных значений (–––– – i; – _· – – p; ········· – u)

Пусть , тогда

.

В цепи с R ток и напряжение совпадают по фазе.

Закон Ома для цепи с R .

Пусть р = iu – мгновенная мощность, тогда

;

означает, что электрическая энергия все время потребляется приемником.

Цепь с индуктивностью L показана на рис. 1.14.

Рис. 1.14. Электрическая цепь с L (а), ее векторная диаграмма (б)

и графики (в) мгновенных значений (–––– – i; – _· – – p; ········· – u)

ЭДС самоиндукции

.

Пусть , тогда

e = – u ;

.

В цепи с L ток отстает по фазе от напряжения на .

З

Рис. 1.15. К понятию X_L

акон Ома для цепи сL , где – индуктивное сопротивление.

, т.е. цепь с индуктивностью активной мощности не потребляет.

В цепи с индуктивностью в первую четверть периода электрическая энергия потребляется и запасается в виде энергии магнитного поля, во вторую четверть периода энергия отдается обратно в цепь и т.д., при этом .

Цепь с емкостью С представлена на рис. 1.16.

Рис. 1.16. Электрическая цепь с C (а), ее векторная диаграмма (б)

и графики (в) мгновенных значений (–––– – u; – _· – – p; ········· – i)

Пусть ; ; . В цепи с емкостью напряжение отстает от тока по фазе на  .

.

З

Рис. 1.16. К понятию X_C

акон Ома для цепи сC , где – ёмкостное сопротивление.

.

Происходит колебательный обмен энергии между источником и приемником. При этом Р_ср = 0.

1.6.6. Цепь с последовательным соединением r, l, c

(рис. 1.17)

Рис. 1.17. Цепь с последовательным соединением R, L, C (а) и векторные диаграммы: б – цепь носит активно-индуктивный характер; в – цепь носит активно-емкостный характер

; .

В зависимости от соотношения U_L и U_C (x_L и x_C) цепь может носить активно-индуктивный, активно-емкостный или чисто активный характер. Последний случай рассмотрим отдельно. Из векторной диаграммы имеем

;

.

Закон Ома для цепи с :

,

здесь Z – полное сопротивление.

1.6.7. Треугольники напряжений, сопротивлений и мощностей

Из векторной диаграммы цепи с последовательным соединением имеем треугольник напряжений:

,

,

где cos  – коэффициент мощности, .

Согласно закону Ома ; ; .

Делим каждую сторону треугольника напряжений на ток и получаем треугольник сопротивлений:

; ;

; .

Умножаем каждую сторону треугольника напряжений на ток, и получаем треугольник мощностей:

; ;

; ,

здесь P – активная мощность [Вт]; S – полная мощность, вырабатываемая источником [ВА]; Q – реактивная мощность [ВАр].

Коэффициент мощности показывает, насколько эффективно и рационально используется энергия.Р характеризует ту часть энергетического процесса, в которой электрическая энергия потребляется приемником и преобразуется в другие виды энергии, т.е. в полезные дела. Q характеризует ту часть энергетического процесса, которая связана с изменением энергии электрического поля емкости или магнитного поля индуктивности. Реактивная мощность не совершает полезной работы, т.к. электрическая энергия не преобразуется в другие виды энергии.