Знаки у частичных токов берем с учетом их направления.

1.6. Цепи переменного тока

Пусть для передачи энергии мощностью P = 1000 Bт есть два варианта:

1) В, А;

2) В, А.

Первый вариант предпочтительнее для передачи энергии, так как в этом случае существенно меньше потери на нагрев проводов ЛЭП .

Таким образом, передавать энергию выгодно при высоком напряжении, а потреблять, из соображений техники безопасности, при низком.

Основная причина, по которой применяют переменный ток, – необходимость преобразования электрической энергии в энергию высокого напряжения перед ее передачей и обратно после ее передачи. Эти преобразования сравнительно просто делаются только в цепях переменного тока.

Переменный ток – это такой изменяющийся по величине и направлению ток, среднее значение которого за период равно нулю. Наиболее предпочтительный закон изменения тока – синусоидальный.

Преимущества переменного синусоидального тока:

• более высокие энергетические показатели работающих на нем машин;

• более простой расчет электрических цепей;

• производная от синусоидальной функции есть синусоидальная функция.

1.6.1. Основные параметры синусоидальной функции

П

Рис. 1.10. Мгновенные значения

тока и напряжения

устьi и u – мгновенные значения тока и напряжения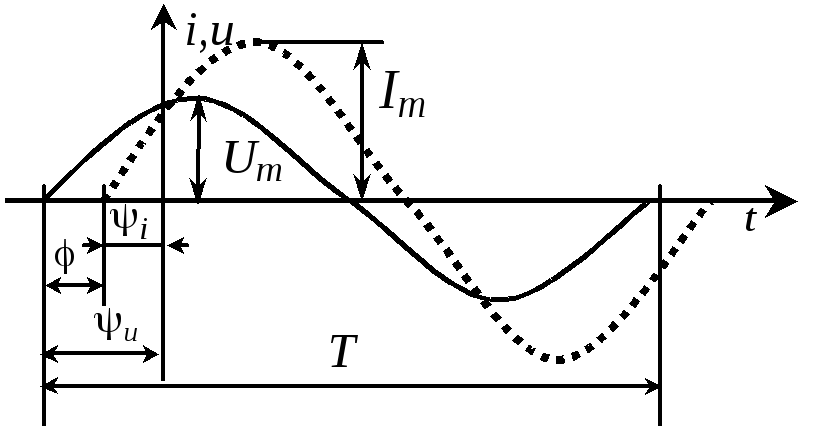: , , где и– максимальные амплитудные значения тока и напряжения (рис. 1.10).

, где f – частота, Т – период;  – круговая частота, =

= 2f; и – начальные фазы тока и напряжения,  – угол сдвига фаз, – фаза. ЕслиГц, то с^–1.

1.6.2. Получение синусоидальной эдс в промышленности

Переменную синусоидальную ЭДС в промышленности получают с помощью синхронных генераторов (рис. 1.11).

Магнитное поле создаётся ротором. При вращении ротора в проводниках обмотки статора возникает ЭДС – , где l – длина проводника обмотки статора; V – скорость; V и l – const.

Так как при вращении ротора индукция В изменяется по закону, то.

1.6.3. Действующее и среднее значение переменного тока

Под действующим значением переменного тока понимают значение постоянного тока I, который, проходя по резистору, выделяет в нем такое же количество тепла, что и действительный синусоидальный ток i = I_msin().

Обозначим W(–) энергию, выделяемую при протекании постоянного тока, W(~) энергию, выделяемую при протекании переменного тока.

;

;

; ;

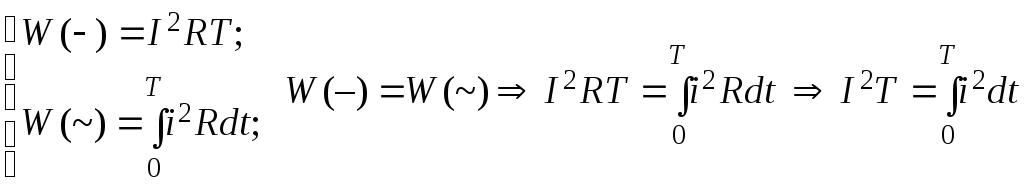действующее значение тока;

действующее значение напряжения ;

действующее значение ЭДС .

Определим среднее значение тока I_ср:

.

; – средние значения ЭДС и напряжения соответственно;

.

1.6.4. Изображение синусоидальной функции векторами

Рис. 1.12. Изображение синусоидальных функций векторами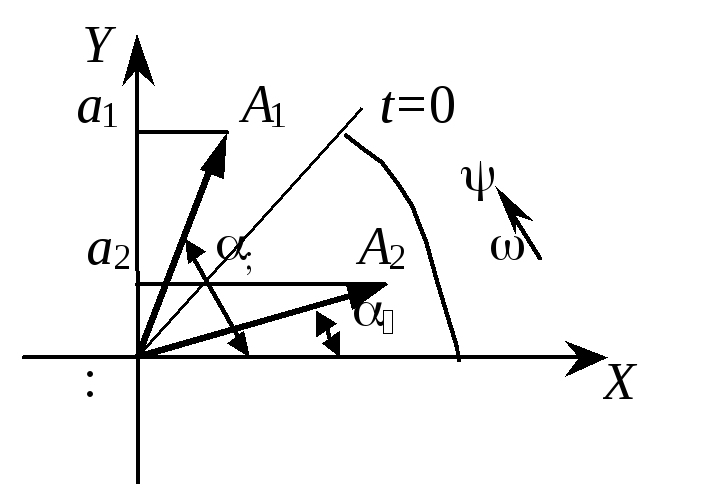

Пусть есть радиус-вектор ОА₂, длина которого соответствует амплитуде ЭДС Е_m: . Его проекция на вертикальную ось

.

Пусть , т.е. вектор вращается, тогда

.

Если при t = 0 радиус-вектор расположен под углом  к оси OX, то

; .

мгновенное значение синусоидальных ЭДС

.

Таким образом, проекция вращающегося вектора на вертикальную ось описывается синусоидальным законом, т.е. каждому вращающемуся вектору можно поставить в соответствие синусоидальную функцию и, наоборот, каждой синусоидальной функции – вращающийся вектор. Вектора изображают при t = 0.

Для перехода от мгновенного значения к вектору амплитуды необходимо в качестве длины вектора взять амплитуду, а в качестве угла от горизонтальной оси – начальную фазу. 

Вектор действующего значения короче вектора амплитудного значения в раз.

Особенностями анализа цепей переменного тока являются следующие:

1. В цепях переменного тока необходимо учитывать влияние индуктивности и емкости.

; .

2. В цепях переменного тока законы Ома и Кирхгофа без предварительного вывода можно применять только для мгновенных значений токов и напряжений или соответствующих им векторов.