2.2. Сумматоры.

Комбинационные сумматоры находят широкое применение в арифметических устройствах вычислительных систем.

Двоичным сумматором называется логическое устройство (узел), выполняющее операцию сложения двух двоичных чисел.

В сумматорах параллельного действия слагаемые числа поступают на входы сумматора в параллельном коде, результат выдается параллельным же кодом на его выходах.

Таким образом, комбинационный сумматор n-разрядных двоичных чисел представляет собой дискретной устройство, имеющее 2n входов и n выходов. Такое устройство называется многоразрядным сумматором. Многоразрядный сумматор представляет собой совокупность так называемых одноразрядных сумматоров, каждый из которых формирует значение только одного из разрядов суммы.

Одноразрядные сумматоры можно классифицировать по количеству входов на следующие виды:

- двухвходовые, именуемые полусумматорами;

- трехвходовые, именуемые полными сумматорами.

Одноразрядные сумматоры применяются для обработки последовательных кодов, а соответствующим образом соединенная совокупность таких сумматоров образует многоразрядный сумматор, предназначенный для обработки параллельных кодов.

Одноразрядный полусумматор (HS) имеет два входа и два выхода (рис. 2.2). С выхода S снимается сигнал суммы (S), а с выхода Р - сигнал переноса (Р).

Функционирование полусумматора описывается таблицей соответствия (истинности), изображенной в виде табл. 2.1

Таблица 2.1

X1	X2	S	P
0	0	0	0
0	1	1	0
1	0	1	0
1	1	0	1

Из табл. 2.1 получаем:

Видим, что логическая функция суммы S соответствует функции “неравнозначность” (сложение по модулю 2), а логическая функция переноса Р - функции “конъюнкция”.

Построив эти функции в заданном базисе, получим функциональную схему полусумматора. Схема HS в базисе И, ИЛИ, НЕ представлена на рис. 2.3,а.

Для сокращения числа логических элементов проведем некоторые преобразования логических функций S и Р. Выразим функцию S в КНФ (методом двойной инверсии или используя распределительный закон) и проведем преобразования:

.

Итак получили:

Функциональная схема такого полусумматора представлена на рис. 2.3, б (в базисе И, ИЛИ, НЕ).

Полусумматоры могут применяться как сумматоры по модулю 2. В этом случае используется один выход S. Во многих сериях ИМС полусумматор имеется как отдельный логический элемент.

Полным сумматором (SM) называется устройство (рис. 2.4), предназначенное для сложения трех однозарядных двоичных чисел и имеющее 3 входа и 2 выхода. При разрядном сложении двух многозарядных чисел приходится учитывать сигнал переноса предыдущего разряда (Р_i-1), который в полном сумматоре и подается на третий вход (х₃). На выходе S вырабатывается, как и в полусумматоре, сигнал суммы (S), а на выходе Р - сигнал переноса (Р). Функционирование полного сумматора описывается таблицей соответствия (табл. 2.2), из которой получаем:

Схема сумматора, построенная по этим выражениям в базисе И, ИЛИ, НЕ, представлена на рис. 2.5.

Таблица 2.2

X1	X2	X3	S	P
0	0	0	0	0
0	0	1	1	0
0	1	0	1	0
0	1	1	0	1
1	0	0	1	0
1	0	1	0	1
1	1	0	0	1
1	1	1	1	1

Так как быстродействие комбинационных схем определяется временем задержки входных сигналов логическими элементами, т.е. количеством элементов в цепях распространения сигналов, то приведенная схема полного сумматора по быстродействию наилучшая, хотя и обладает аппаратурной избыточностью.

Если в составе серии ЛЭ имеются готовые микросхемы полусумматоров, то целесообразно использовать их для построения полного сумматора, хотя схема последнего в этом случае не будет оптимальной.

Для реализации схемы полного сумматора на полусумматорах преобразуем логические функции S и Р следующим образом.

Первый полусумматор (HS1) имеет входы х₂и х₃, второй (HS2) - входы х₁и S_HS1.

Соответствующая этим функциям структурная схема полного сумматора изображена на рис. 2.6.

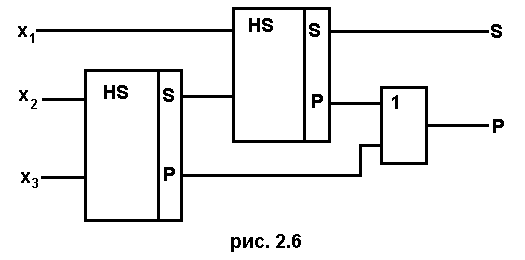
С помощью однозарядных сумматоров можно построить суммирующие устройства для сложения многоразрядных двоичных чисел, которые могут быть последовательного или параллельного действия.

Наиболее употребительны сумматоры параллельного действия, так называемые многоразрядные сумматоры, которые строятся из полных сумматоров, соединенных определенным образом так, что сигнал (выход Р) переноса предыдущего разряда поступает на третий вход последующего разряда (рис. 2.7). На первый и второй входы каждого полного сумматора поступают цифры одноименных разрядов слагаемых чисел (кодов).

Время суммирования определяется временем передачи сигнала переноса от младшего разряда к старшему:

,

где - время образования суммы в полном сумматоре;

n - разрядность сумматора;

t_n- время распространения переноса в одном разряде.

Поскольку , то быстродействие суммирующего устройства в основном зависит от времени распространения сигнала переноса.

Быстродействие суммирующего устройства параллельного действия значительно выше, чем последовательного.

Кроме комбинационных суммирующих устройств (подр. 2.2), применяются накапливающие суммирующие устройства (сумматоры с памятью), которые не только суммируют слагаемые, но и запоминают полученную сумму. В качестве элементов памяти, как правило, применяются триггеры со счетным входом. Одноразрядный накапливающий сумматор содержит схему ИЛИ на 3 входа и триггер со счетным входом, у которого нулевой выход является инверсным динамическим (рис. 2.8).

Слагаемые х₁, х₂и х₃суммируются (поступают на вход схемы ИЛИ) поочередно. х₁и х₂- это значения одноименных зарядов суммируемых кодов. В качестве третьего слагаемого х₃используется сигнал переноса (Р_i-1) соседнего младшего разряда. Результат суммирования запоминается в триггере, а сигнал переноса Р передается в соседний старший разряд. Работу однозарядного накапливающего сумматора поясним по временной диаграмме (рис. 2.10). Сумматор функционирует в соответствии с таблицей истинности (табл. 2.2). С приходом импульса сброса “Уст. 0” триггеры всех разрядов сумматора устанавливаются в соответствие 0. Сигнал сброса является преобладающим (более длительным) по сравнению с другими импульсами.

С приходом импульса х₁=I триггер устанавливается в состояние I (S=I). С приходом импульса х₂=I триггер переходит в состояние 0 и формируется сигнал переноса в старший разряд (S=0, P=I). С приходом импульса х₃=I триггер снова переходит в состояние I (S=I). Сигнал переноса при этом не формируется, но триггер старшего разряда запомнил сигнал переноса P=I, который поступил на его вход при суммировании двух сигналов х₁и х₂. Таким образом, и в случае суммирования трех сигналов получаем S=I, P=I, что и следует из таблицы соответствия.

Многоразрядные накапливающие сумматоры строятся из одноразрядных накапливающих сумматоров так же, как и многоразрядные комбинационные сумматоры параллельного действия (см. рис. 2.7)

При этом быстродействие сумматора также будет зависеть от способов организации цепей переноса. Однако при прочих равных условиях накапливающие сумматоры обладают более низким быстродействием, чем комбинационные суммирующие устройства, что объясняется последовательным вводом слагаемых и сигналов переноса, а также потерей времени на перевод триггеров из одного устойчивого состояния в другое.