1.4. Построение функциональных схем дискретных устройств на бесконтактных логических элементах.
Известно, что дискретные устройства могут строиться на различных наборах логических элементов. Важно, чтобы эти наборы были полными, т.е. реализовывали бы функционально полную систему логических функций.
Напомним, что к наиболее распространенным функционально полным наборам логических элементов относятся следующие наборы:
1) из трех элементов И, ИЛИ, НЕ (основной набор);
2) из двух элементов И, НЕ;
3) из двух элементов ИЛИ, НЕ;
4) из одного элемента ИЛИ-НЕ (НИ-НИ, элемент Пирса);
5) из одного элемента И-НЕ (элемент Шеффера).
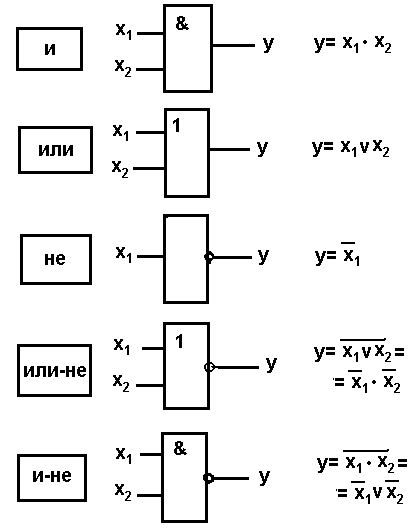
Логические элементы И, ИЛИ, НЕ реализуют соответственно функции конъюнкции, дизъюнкции и отрицания (инверсии) и обозначаются по ГОСТу как показано на рис. 1.15.
Универсальный элемент ИЛИ-НЕ реализует функцию отрицания дизъюнкции (стрелка Пирса). Выходной сигнал равен произведению инверсий входных сигналов. Универсальный элемент И-НЕ реализует функцию отрицания конъюнкции (штрих Шеффера). Выходной сигнал равен сумме инверсий входных сигналов.
Любая
логическая функция представляет собой
набор символов, связанных знаками
дизъюнкции, конъюнкции и инверсии.
Других операций нет. Поэтому возможность
реализации любой логической функции с
помощью основного набора логических
элементов (И, ИЛИ, НЕ) очевидна, а с помощью
остальных наборов - не очевидна.
С помощью универсального приема двойного инверсирования можно показать, как реализуются основные операции алгебры логики (конъюнкция, дизъюнкция и инверсия) на функционально полных наборах, состоящих из одного и двух логических элементов.
Рис 1.5.
Рассмотрим, например, реализацию основных операций алгебры логики на наборе ИЛИ-НЕ.
Необходимо рассмотреть реализацию трех основных функций.
Операция НЕ. В элементе ИЛИ-НЕ задействуется только один вход, тогда элемент работает как инвертор (рис. 1.16). Используется один элемент ИЛИ-НЕ.
Операция И.Воспользуемся приемом двойной инверсии:
Видим, что следует реализовать функцию отрицания дизъюнкции для двух инверсных сигналов (рис. 1.7). Необходимы три элемента ИЛИ-НЕ.
Операция ИЛИ.
Имеем инверсию от инверсии дизъюнкции, т.е. сначала ИЛИ-НЕ, потом НЕ. Для реализации необходимы два элемента ИЛИ-НЕ (рис. 1.18).
Рассмотрим реализацию основных операций алгебры логики на наборе И-НЕ.
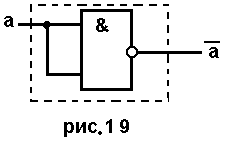
Операция НЕ.В элементе И-НЕ задействуется только один вход, тогда элемент работает как инвертор (рис. 1.19). Используется один элемент И-НЕ.
Операция
И.Воспользуемся приемом двойной
инверсии.
Имеем инверсию от инверсии конъюнкции,
т.е. сначала И-НЕ, потом НЕ. Для реализации
требуется 2 элемента И-НЕ (рис. 1.20).
Операция ИЛИ.
Имеем инверсию от конъюнкции инверсий,
т.е. сначала два раза НЕ, а затем И-НЕ
(рис. 1.11).
Аналогичным образом получаем реализацию основных операций алгебры логики для остальных функционально полных наборов (рис. 1.12).
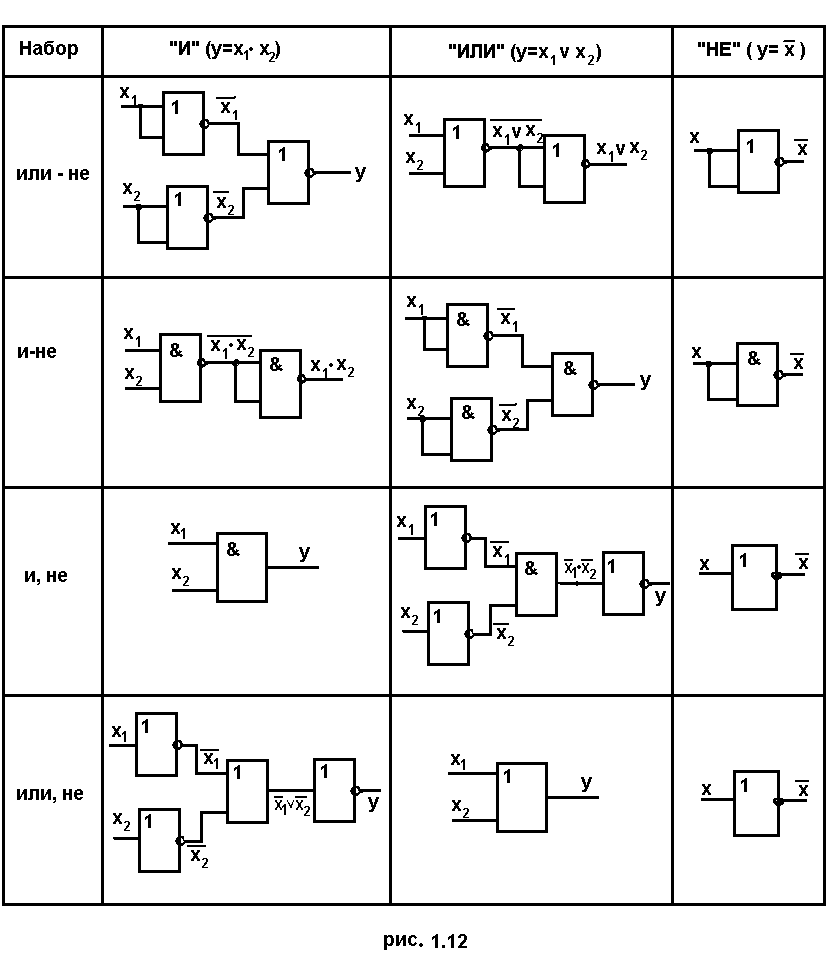
В случае большого числа переменных соответственно увеличивается количество входов или входных инверторов.
Классическая методика построения функциональной схемы ДУ по логической функции, которую оно реализует, заключается в следующем:
- по известной логической функции построить структурную схему ДУ в основных операциях алгебры логики (И, ИЛИ, НЕ);
- выбрать функционально полный набор БЛЭ для реализации ДУ;
- перейти от структурной схемы к функциональной с учетом правил реализации основных операций на выбранном наборе элементов;
- произвести упрощения схемы.
Упрощения производятся, как правило, за счет исключения из схемы двух последовательно стоящих инверторов.
Рассмотрим примеры построения функциональной схемы БДУ на наборах И-НЕ, ИЛИ-НЕ.
Пример 5. Даны условия работы ДУ в виде логической функции:
.
Построить функциональную схему.
Строим структурную схему ДУ (рис. 1.13), затем по правилам реализации операций (см. рис. 1.20) - функциональную схему ДУ на элементах И-НЕ (рис. 1.14).
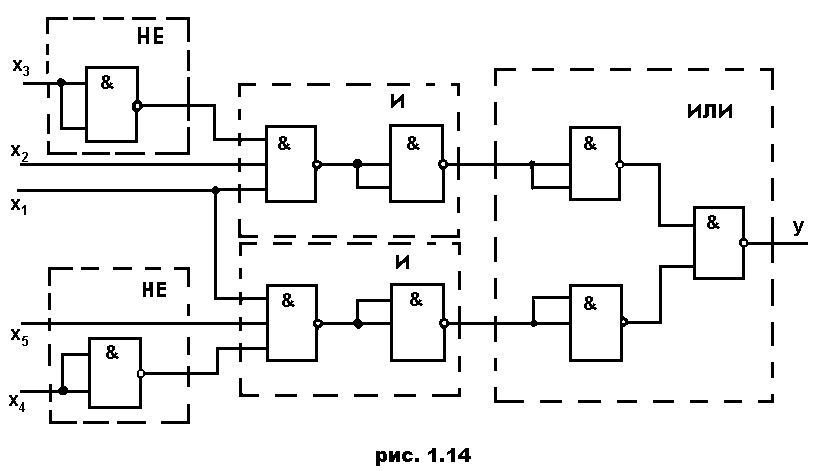
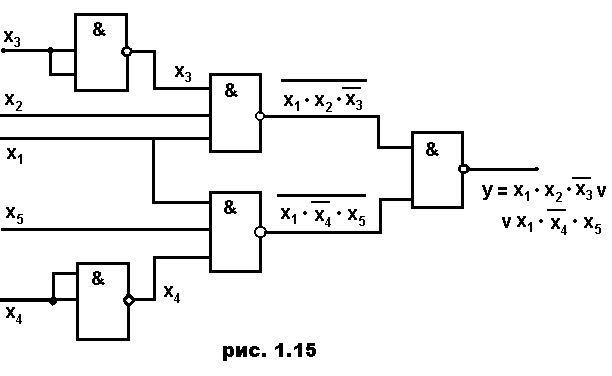
Последовательно соединенные два инвертора компенсируют друг друга и могут быть из схемы исключены. После упрощения получаем окончательную функциональную схему (рис. 1.15), состоящую из 5 элементов И-НЕ.
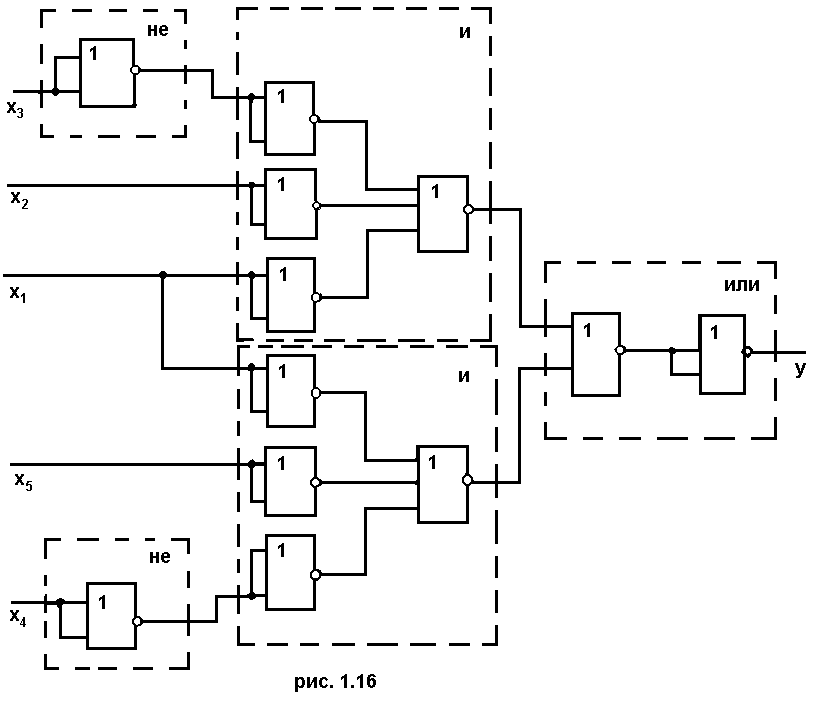
Теперь построим для этого же примера функциональную схему на элементах ИЛИ-НЕ. Используем ту же структурную схему (см. рис.1.13). Получаем схему (рис. 1.16), содержащую 12 элементов ИЛИ-НЕ.
Путем
исключения последовательных инверторов
и объединения сигнала
,
схема сокращается на 5 элементов и
остается 7 элементов ИЛИ-НЕ (рис. 1.17).
Изложенная методика построения функциональной схемы ДУ является универсальной, т.е. всегда лает правильное решение - работоспособную схему, но, как правило, слишком громоздкую.
В инженерной практике обычно, обладая известным навыком преобразования логических функций, выполняют этап преобразования исходного аналитического выражения (условия работы ДУ, полученные в результате абстрактного синтеза) к виду, удобному для реализации на выбранном наборе БЛЭ.
В результате этого этапа исходная функция записывается сразу в операторах И-НЕ для реализации на сериях интегральных элементов с базовым элементом И-НЕ, либо в операторах ИЛИ-НЕ для реализации на сериях БЛЭ “Логика”, “Логика-Т” и т.д. с базовым элементом ИЛИ-НЕ.
Для преобразования функции, как правило, пользуются универсальным приемом двойного инверсирования.
Двойное инверсирование функции, записанной в ДНФ, дает форму операторов И-НЕ, а двойное инверсирование функции, записанной в КНФ, дает форму операторов ИЛИ-НЕ.
Таким образом, если для построения ДА принят набор И-НЕ, то исходную функцию (условия работы ДА), полученную в результате абстрактного синтеза, следует преобразовать в ДНФ, а если принят набор ИЛИ-НЕ, то исходную функцию следует преобразовать в КНФ.
Пример 12. Построить
функциональную схему БДУ на наборе
ИЛИ-НЕ в соответствии с условиями работы
Условия работы (исходная функция) уже
написаны в КНФ. Применяем прием двойного
инверсирования:
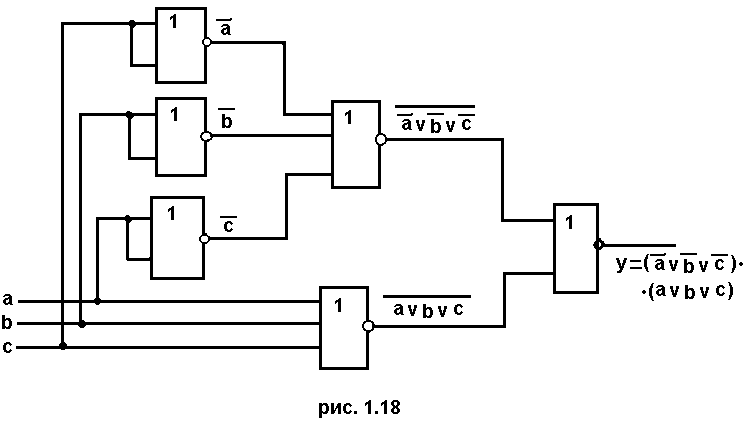
Получили выражение, записанное в операторах ИЛИ-НЕ. Функциональная схема ДУ, построенная по данному выражению, изображена на рис. 1.18.
Если нужно построить
эту функцию на наборе И-НЕ, то исходную
функцию следует привести к ДНФ, а затем
исследовать прием двойной инверсии.
Однако эту функцию можно упростить по
правилу: если ЛФ записанным в ДНФ (КНФ),
а нужно ее реализовать на наборе ИЛИ-НЕ
(И-НЕ), то прием двойного инверсирования
применяют дважды - сначала над каждым
членом исходной функции, затем над самой
функцией. Построим ЛФ
на наборе И-НЕ:
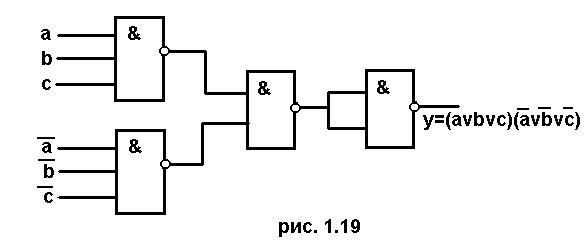
Схема приведена на рис. 1.19 (считаем, что известные сигналы уже получены).
Пример 13.
Построить функциональную схему БДУ на
наборе И-НЕ в соответствии с условиями
работы
.
Условия работы (исходная функция) уже
записаны в ДНФ. Применяем прием двойного
инверсирования:
.
Получили выражение, записанное сразу в операторах И-НЕ. Очевидно, что функциональная схема ДУ имеет вид, изображенный на рис. 1.20.
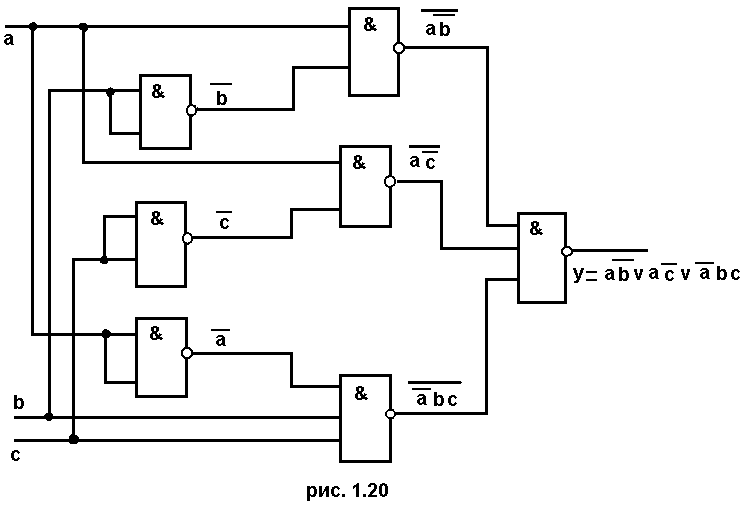
Попробуем еще преобразовать исходное выражение в направлении уменьшения числа операций ИЛИ (так как базовый элемент принят И-НЕ):
.
Полученное выражение также записано в операторах И-НЕ. Функциональная схема его представлена на рис. 1.21.
Заметим, что в подобных случаях функциональные схемы удобно строить “с конца” аналитического выражения.
Сравнивая рис. 1.30 и 1.31, видим, что достигнута экономия в два элемента И-НЕ.
В случае синтеза многовыходных ДА без памяти следует после получения минимизированных выражений для нахождения сигналов на каждом выходе провести преобразования системы уравнений с целью объединения одинаковых групп членов, членов или их частей в разных уравнениях, а после этого строить функциональную схему ДА.
Следующий этап - физический синтез. Он имеет своей целью переход от функциональной схемы структуры проектируемого ДУ к принципиальной электрической схеме. На этом этапе выбираются типы бесконтактных элементов, обеспечиваются дополнительные требования: надежность, технологичность, удобство контроля и т.д.