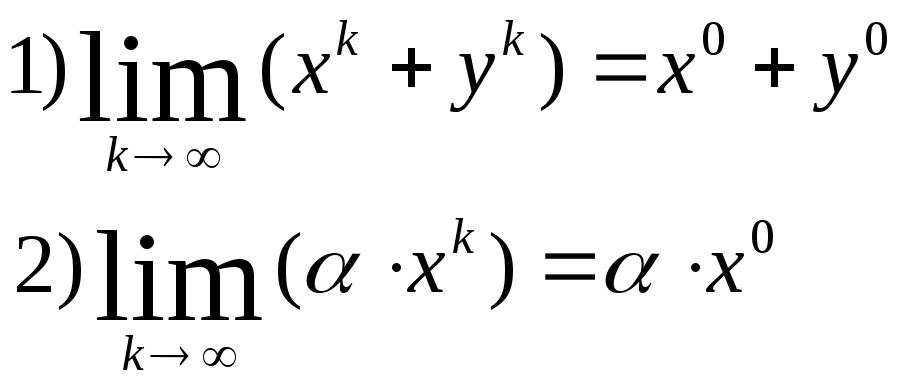Программирование / си++ / ЛЕКЦИИ АСУ-03 за 1й курс / II cemecTP / Шпоры по матану / 11-15 / моё

(11) ТОЧЕЧНЫЕ МНОЖЕСТВА НА ПЛОСКОСТИ И В ПРОСТРАНСТВЕ; ОТКРЫТЫЕ, ЗАМКНУТЫЕ И СВЯЗАННЫЕ МНОЖЕСТВА.

Множества в Rⁿ Понятие множества, не определяется, но может быть пояснено при помощи примеров (БСЭ) Шаром радиуса r в точке Х0 наз. Такое мн-во, в к-ром вып. усл:

где - координаты центра окр.

Открытое мн-во Мн-во X из R наз открытым, если вместе с любой т. Х0 в нем содержащейся, оно содержит некоторый шар радиусом r с центром в этой точке.

открытое множество образовано только внутренними точками

Замкнутое мн-во замкнутым наз такое мн-во, к-рое содержит все свои пограни

Ввнешняя точка Т. Х0 наз внешней для мн-ва, если она не содержится в этом мн-ве и сущ. круг(шар), не лежащий в нем.

Граничные точки Т. Х0 наз граничной для мн-ва Х, если в любом круге(шаре) имеются как внутренние, так и внешние точки этого мн-ва.

Окрестность Окр. Т. Х0 наз всякое открытое мн-во, содержащее эту точку.

Связанное мн-во мн-во Х из Rn наз связанным, если люб. Его точки х1,х2 можно соединить непрерывной кривой, содержащейся внутри этого мн-ва. Всякое открытое связанное мн-во наз областью

(12)ПОНЯТИЕ ФУНКЦИИ 2-Х И НЕСКОЛЬКИХ ПЕРЕМЕННЫХ, СПОСОБЫ И ЗАДАНИЯ.

Функция двух переменных Если каждой паре (х,у) значений двух, независимых друг от друга, переменных величин х и у, из некоторой области их измерения D соотв опр. Значение величины z, то z есть функция двух независимых переменных. Обозначается z=f(x,y)

Областью определения функции наз совокупность пар (х,у) значений х и у, при к-рых определяется ф-ция z=f(x,y)

Способы задания ф-ции: 1-аналитически (ур-нием), 2-таблично (табл.значений), 3-графиком или алгоритмом.

Функция нескольких переменных – определение аналогично опр. Ф-ии 2-х переменных

(13) ПОНЯТИЯ ПРЕДЕЛА ПОСЛЕДОВАТЕЛЬНОСТИ В R" И ПРЕДЕЛА ФУНКЦИИ N ПЕРЕМЕННЫХ

Предел последовательности. В m-мерном пространстве дана некоторая последовательность точек . Пределом этой последовательности будет нек. точка , если коорд. точки Мn порознь стремятся к соотв. коорд.точки M0

Предел ф-ции Ф-ция f(x1,...xm) имеет пределом число А при стремлении переменных х1,…,хм ,соответственно к а1,…,ам (M->M0) если для каждого числа найдется такое ,что при

Опр. по КОШИ:

Опр. по Гейне:

(14) ОСНОВНЫЕ СВОЙСТВА ПРЕДЕЛОВ ПОСЛЕДОВАТЕЛЬНОСТЕЙ И ФУНКЦИЙ В R"

(15) НЕПРЕРЫВНОСТЬ ФУНКЦИЙ N ПЕРЕМЕННЫХ. СВОЙСТВА ФУНКЦИЙ И ПЕРЕМЕННЫХ, НЕПРЕРЫВНЫХ В ТОЧКЕ, В ОТКРЫТОЙ ОБЛАСТИ И ЗАМКНУТОМ МНОЖЕСТВЕ.

Непрерывность ф-и Ф-я непрерывна в точке Х⁰ , если: 1-она определена в U(X⁰) 2- 3-A=f(X⁰)

Св-ва 1-Если f(x,y) определена и непрерывна в замкнутой и ограниченной области D, то в этой области найдется по крайней мере одна точка N(Х₀,Y₀) такая, что для всех других точек области будет выполняться и по крайней мере одна точка N’(Х₀^’,Y₀^’) такая, что для всех других точек области будет выполняться 2- Если f(x,y) определена и непрерывна в замкнутой и ограниченной области D и если М и m – наиб и наим знач ф-и в области, то для любого числа а, удовл усл m<a<M, найдется в области такая точка N(Х₀',Y₀'), что f(Х₀',Y₀')=а (это была т. коши о промежуточном значении) Следствие из (2)-Если f(x,y) определена и непрерывна в замкнутой и ограниченной области D и принимает как положительные, так и отрицательные значения, то внутри области найдутся точки, в к-рых ф-я обращается в 0. 3-арифм. операции над непрерывн в D ф-ями сохраняют непрерывность 4-если ф-я n-переменных непрерывна в открытой области D и все её координаты X_i явл ф-ями m-переменных в откр. обл. G, то суперпозиция этих ф-й так же непрерывна в обл G, т.е.