Программирование / лаб3

Задание.

Задание на лабораторную работу: построить имитационную модель Системы Массового Обслуживания с отказами и полной взаимопомощью между каналами обслуживания. Исследовать влияние числа каналов обслуживания и загрузки системы на вероятностные характеристики системы.

Исходные данные:

n (число каналов обслуживания) = 6 (изменяем в ходе исследования)

(загрузка системы , где - интенсивность поступления заявок, - интенсивность обслуживания каждого канала) (изменяем в ходе исследования)

Рассчитать:

1. вероятность простоя системы;

2. вероятность полной загрузки системы;

3. вероятность отказа в обслуживания.

Выполнение.

Примем за состояние системы число заявок, находящихся в данный момент на обслуживании и рассмотрим 3 случая с различным числом каналов обслуживания.

Построим для общего случая граф и систему:

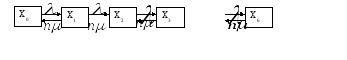
В связи с тем, что входящий поток заявок принимается Пуассоновским, как и поток обслуживания, вместо системы интегро-дифференциальных уравнений имеем систему алгебраических уравнений:

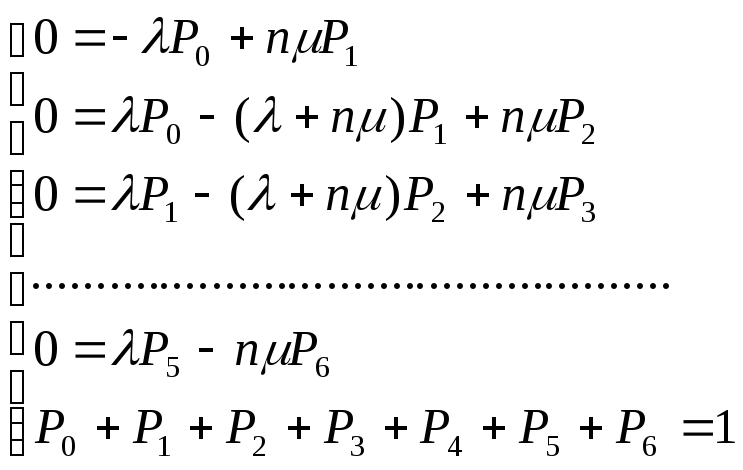
Моделируем поступление заявок по Пуасонновскому распределению:

-входящий поток -поток обслуживания

Считаем общее количество заявок N_ОБЩЕЕ , а также количество отказов N_{ОТКАЗОВ}, время занятости каналов T_{ЗАНЯТОСТИ}. Тогда вероятностные характеристики можно рассчитать по следующим формулам представленным ниже

Найдем вероятностные характеристики системы:

1. Вероятность простоя -

2. Вероятность полной загрузки

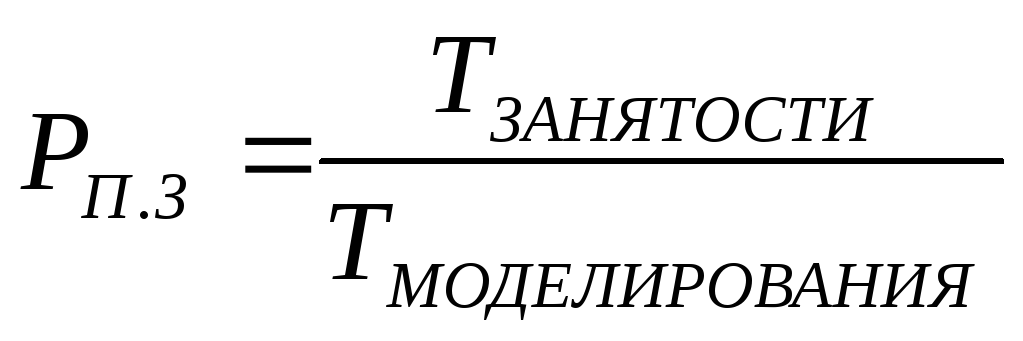
3. вероятность отказа в обслуживания

При моделировании получены следующие результаты: 1) n=6

Характеристика	Значение
Вероятность простоя системы	0,879353
Вероятность полной загрузки системы	0,121647
Вероятность отказа в обслуживании	0,000006

2) n=4

Дальнейшие действия аналогичны:

Найдем вероятностные характеристики системы:

При моделировании получены следующие результаты:

Характеристика	значение
Вероятность простоя системы	0,843434
Вероятность полной загрузки системы	0,156566
Вероятность отказа в обслуживании	0,001435

3) n=8

Найдем вероятностные характеристики системы:

При моделировании получены следующие результаты:

Характеристика	Значение
Вероятность простоя системы	0,977091
Вероятность полной загрузки системы	0,022909
Вероятность отказа в обслуживании	0,000002

Изучим влияние загрузки системы на вероятностные характеристики. Для этого дадим приращение и снова просчитаем вероятностные характеристики для систем с n= 4, 6, 8.

Соответствующие значения n=4:

Характеристика	Значение при =0,7	Значение при =0,9
Вероятность простоя системы	0,831164	0, 813328
Вероятность полной загрузки системы	0,178836	0,185661
Вероятность отказа в обслуживании	0,000697	0,002102

Для n=6

Характеристика	Значение при =0,7	Значение при =0,9
Вероятность простоя системы	0,885532	0,839465
Вероятность полной загрузки системы	0,114468	0,160535
Вероятность отказа в обслуживании	0,000003	0,000011

Для n=8

Характеристика	Значение при =0,7	Значение при =0,9
Вероятность простоя системы	0,920540	0,897876
Вероятность полной загрузки системы	0,079460	0,102124
Вероятность отказа в обслуживании	0,00000002	0,00000002

Листинг программы на языке TURBO PASCAL 7.0

const

n_kanalov=6;

ro=0.8;

xi=ro/n_kanalov;

lambda=3;

mu=xi/lambda;

time_t=1000000;

var

n_svob_mest,p:integer;

vypolneno:real;

kolvo,i,ok,obs,otkaz:integer;

t:longint;

t_z0,t_z,t_obs:real;

n:array[1..n_kanalov] of real;

t_zan:array[1..n_kanalov] of real;

n_vyp:array[1..n_kanalov] of integer;

Potkaz,Ppz,Pprost:real;

n_zero:array[1..l] of integer;

begin

randomize;

t_z0:=0;

kolvo:=0;

obs:=0;

otkaz:=0;

vypolneno:=0;

for i:=0 to n_kanalov do

begin

n_vyp[i]:=0;

t_zan[i]:=0;

end;

for t:=0 to time_t do

begin

for i:=1 to n_kanalov do

begin

if ((t>n[i])AND(n[i]<>0)) then

begin

n[i]:=0;

vypolneno:=vypolneno+1;

end;

end;

n_svob:=0;

for i:=1 to do n_zero[i]:=0;

p:=1;

for i:=1 to n_kanalov do

begin

if (n[i]=0) then

begin

inc(n_svob_mest);

n_zero[p]:=i;

inc(p);

end;

end;

if (n_svob_mest>=1)and(n_svob_mest<=n_kanalov) then begin

t_obs:=-1000/(n_kanalov*mu)*ln((random(1000)+1)/1000);

for i:=1 to l do

begin

n[n_zero[i]]:=t+t_obs;

t_zan[n_zero[i]]:=t_zan[n_zero[i]]+t_obs;

n_vyp[n_zero[i]]:=n_vyp[n_zero[i]]+1;

ok:=1;

end;

inc(obs);

end;

end;

if (t>=t_z0) then

begin

t_z:=-1000/lambda*ln((random(1000)+1)/1000);

t_z0:=t_z0+t_z;

inc(kolvo);

n_svob:=0;

for i:=1 to l do n_zero[i]:=0;

p:=1;

for i:=1 to n_kanalov do

begin

if (n[i]=0) then

begin

inc(n_svob);

n_zero[p]:=i;

inc(p);

end;

end;

if (n_svob>=l) then begin

t_obs:=-1000/(l*mu)*ln((random(1000)+1)/1000);

for i:=1 to l do

begin

n[n_zero[i]]:=t+t_obs;

t_zan[n_zero[i]]:=t_zan[n_zero[i]]+t_obs;

n_vyp[n_zero[i]]:=n_vyp[n_zero[i]]+1;

ok:=1;

end;

inc(obs);

end;

if ((n_svob>0)And(n_svob<l)) then begin

t_obs:=-1000/(l*n_svob)*ln((random(1000)+1)/1000);

for i:=1 to n_svob do

begin

n[n_zero[i]]:=t+t_obs;

t_zan[n_zero[i]]:=t_zan[n_zero[i]]+t_obs;

n_vyp[n_zero[i]]:=n_vyp[n_zero[i]]+1;

ok:=1;

end;

inc(obs);

end

else if (ochered1=0) then ochered1:=t_obs

else ok:=0;

if (ok<>1) then inc(otkaz);

end;

end;

Ppz:=0;

for i:=1 to n_kanalov do Ppz:=Pzk+t_zan[i]/time_t;

Pprost:=1-Ppz;

Potkaz:=otkaz/kolvo;

writeln('Вероятность отказа ',Potkaz:5:3);

writeln('Вероятность полной занятости ',Pzk:5:3);

writeln('Вероятность простоя ',Ppk:5:3);

readln;

end.

Выводы по лабораторной работе:

В данной лабораторной работе была построена иммитационная модель системы массового обслуживания с полной взаимопомощью и исследованы вероятностные характеристик системы.

В результате проведенной работы мы выяснили, как вероятностные характеристики системы зависят от числа обслуживающих приборов и загрузки системы. Зависимость осталась той же.Абсолютное отклонение от аналитической модели из лабораторной работы №2 не большое.

Пермский государственный технический университет

Кафедра Автоматики и Телемеханики

Отчет по лабораторной работе №3

Создание имитацтонной модели СМО.

Выполнили студенты гр. АТ-02-2:	Шестопалов А.Н. Чудинов ММ
Проверила:	Данилова С.А.

Пермь, 2005г.