2.2.1 Описание комбинационных устройств с помощью логических уравнений

Логическое выражение – набор узлов, чисел, констант и других логических выражений, разделенных между собой операторами. Логическое уравнение присваивает некоторому узлу или группе значение логического выражения.

В этом примере сигнал на выходе out1управляется «логическим И» сигналовa0и инверсным сигналомa1. Сигнал на выходеout1 управляется «логическим ИЛИ» двух сигналовout1 иb.

На рисунке 2.2 представлена схема устройства, описанного в примере 2.6.

Для получения более подробной информации см. раздел:

• Логические выражения

2.2.2 Объявление узлов

Узел (Node), объявленный в разделе переменных, может быть использован для хранения промежуточного значения выражения.

Узлы очень удобны, если одно и тоже выражение используется большое количество раз, т.к. при этом оно может быть заменено именем узла.

Пример, рассмотренный ниже эквивалентен примеру boole1.tdf, но имеет один выход.

В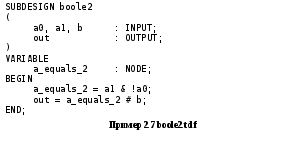этом примере присутствует определение узла с именемa_equals_2и присвоение ему значения выраженияa1 & !a0. Использование узлов позволяет более экономично использовать ресурсы устройства, если эти узлы используются в нескольких выражениях.

На рисунке 2.3 представлена схема устройства, описанного в примере 2.6.

2.2.3 Описание групп

Структура, которая может содержать до 256 членов (или бит) и рассматриваемая как совокупность узлов называется группой. Группа может быть как одномерной, двумерной так и n-мерной (см. пример ниже).

В логических выражениях группа может быть использована для присвоения ей значения некоторого выражения, для присвоения ей некоторой другой группы, некоторого узла, «Лог. 1», «Лог. 0», VCCилиGND. Структура Options может быть использована для указания старшего (MSB – Most Significant Bit) и младшего (LSB – Least Significant Bit) битов группы.

После того как группа определена, ее длину можно не указывать в выражениях. Например, группаa[4..1] в выражениях может быть использована как a[]. В следующем примере будут объявлены несколько групп и показаны простейшие операции с ними:

В данном примере структура Options использована для указания того, что самый правый бит каждой группы является старшим битом. Таким образом, если на вход а[]подать00то на выходеb[] будет значение1(десятичное).

Основные правила использования групп:

• Когда одна группа присваивается другой, равной ей по размеру то каждый бит группы, стоящей справа присваивается соответствующему биту группы, стоящей слева.

В следующем примере каждый бит первой группы присваивается соответствующему биту второй группы. Бит d2присваивается битуq8, битd1– битуq7, а битd0– битуq6:

d[2..0] = q[8..6]

В следующем примере точно также каждый бит первой группы присваивается соответствующему биту второй группы. Бит d1_1присваивается битуq10, битd1_0– битуq9, битd0_1– битуq8, а битd0_0– битуq7:

d[1..0][1..0] = q[10..7]

• Когда группе присваивается некоторый узел, то все биты группы «соединяются» с узлом. В следующем примере d2, d1 и d0 «соединяются» с n:

d[2..0] = n

• Когда группе присваивается значение VCCилиGND, то все биты группы становятся равны присваиваемому значению. В следующем примереd2, d1 и d0 принимают значениеVCC:

d[2..0] = VCC

• Когда группе присваивается какое-либо десятичное значение, например 1, то только младшему биту группы присваивается значение «Лог. 1», всем остальным битам группы присваивается значение «Лог. 0». В следующем примере только d2 станет равным «Лог. 1», а d1 и d0 принимают значение «Лог. 0», т.к 1 = B”001”:

d[2..0] = 1

• Когда две группы различного размера присваиваются друг другу, то при этом должно выполняться следующее условие: число бит группы, стоящей в левой части выражения, должно нацело делиться на число бит группы, стоящей в правой части выражения. При этом присвоение будет происходить так как показано в примере:

a[4..1] = b[2..1]

a4 = b2

a3 = b1

a2 = b2

a1 = b1

Для получения более подробной информации см. разделы:

• Группы

• Использование значений «по умолчанию» для переменных

• Арифметические выражения