4.1. Формула Эйлера – Лагранжа

Дана следующая задача:

–функционал, (4.1)

начальные условия: y(x₀ ) = y₀, y(x₁ ) = y₁ .

Требуется найти такую функцию у(х), проходящую через точки (x₀, y₀) и (x₁ , y₁), при которой данный функционал достигает максимума.

Решим задачу в общем виде.

Предположим, что функция у(х) доставляет экстремум функционалу. Дадим функции у(х) приращение  у такое, что  у = 0 в точках х₀ и х₁ и у  0 в других точках.

Найдем приращение функционала:

. (4.2)

Разложим подынтегральную функцию в ряд Тейлора:

f (x, y+y, y+y) = f (x, y, y) +  f / y  y +  f / y y + R₁, (4.3)

где R₁ – остаток. Тогда, используя (4.3), получим

.

Приращение функции в точке экстремума равно нулю. По аналогии, если функция у(х) доставляет экстремум функционалу, то I = 0, I – главная часть приращения (первая вариация функционала).

I = 0, следовательно,

. (4.4)

Второй интеграл уравнения (4.4) проинтегрируем по частям:

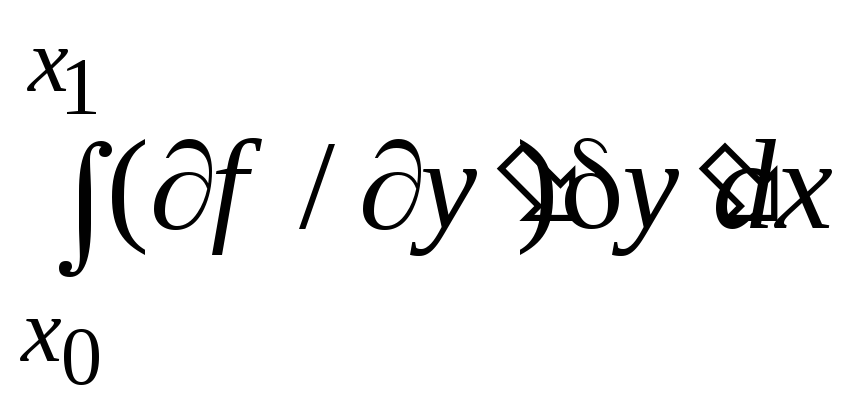= { u = f /y,du = (f /y)_xdx,dv = ydx=

= [(dy/dx)₂ - (dy/dx)₁] dx = [d(y₂ - y₁)/dx] dx = ( y)_x dx = d(y) , v = y } =

x₁ x₁

= ( f / y) y -  (f /y)_x  ydx.

х₁ x₀ x₀

(f /y)y = 0, так как  y в точках х₁ и х₀ равняется нулю. Следовательно,

х₀

x₁ x₁

 (f /y)y dx = -  (f /y)_x  ydx, (4.5)

x₀ x₀

x₁ x₁

I =  ( f / y)  y dx +  ( f / y)_х  y dx = 0, (4.6)

x₀ x₀

x₁

I =  ( f / y - ( f / y)_х )  y dx = 0. (4.7)

x₀

Интеграл (4.7) равен нулю, если равно нулю выражение в скобках.

,

или

(4.8)

– формула Эйлера – Лагранжа (Эйлера).

Чтобы решить задачу вариационного исчисления, нужно решить дифференциальное уравнение Эйлера – Лагранжа (4.7) с граничными условиями: y(x₀) = y₀, y(x₁) = y₁.

Тип экстремума определяется условиями Лежандра:

если f _yy  0, I  min, если f _yy  0, I  max. (4.9)

Пример 4.2.

₀

I =  (y ² - 12ху )dx, y(0) = 0, y(1) = 1.

¹

Требуется найти функцию, доставляющую экстремум функционалу, и определить вид экстремума.

Решение

1. Запишем формулу Эйлера: f_y - d (f_y )/dx = 0,

f = y ² - 12ху, f_y = - 12x, f_y = 2y,

- 12x - (2y)_x = 0.

2. Решим полученное дифференциальное уравнение:

- 12x - 2y = 0,

y = - 6x,

y = - 3x ² + c₁,

y =- x ³ + c₁x + c₂.

Определяем константы: y(0) = c₂ = 0, y(1) = - 1 + c₁ = 1, c₁ = 2,

y(x) = - x³ + 2x.

3. Определяем тип экстремума: f_yy = (2y)_y = 2, следовательно, при найденной функции у(х) функционал достигает максимума.