2.5. Приведение злп к каноническому виду
Процесс приведения задачи к каноническому виду называется нахождением начальной вершины.
Случай 1. Ограничения имеют вид неравенств типа (), ЦФ стремится к минимуму:
a
11x1
+ a12x2
+
+ a1nxn
b1,
a21x1 + a22x2 + + a2nxn b2,
(2.10)
am1x1 + am2x2 + + amnxn bm,
b 1, b 2 ,, b m 0,
Q = P1 x1 + P2 x2 + + Pn xn min .
Задача приводится к каноническому виду путем введения искусственных переменных, которые являются базисными. ЦФ не меняется.
a
11
x1
+
a12
x2
+
+ a1
nxn
+ xn+1
= b1,
a21 x1 + a22 x2 + + a2n xn + xn+2 = b2,
(2.11)
am1 x1 + am2 x2 + + amn xn + xn+m = bm .
Случай 2. Ограничения имеют вид (), ЦФ минимизируется. Кроме того, все коэффициенты ЦФ неотрицательны, а среди bi хотя бы один положительный.
Вводятся искусственные переменные, которые вычитаются из правых частей ограничений. Все коэффициенты ограничений домножаются на (-1).
-
a11
x1
- a12
x2
-
- a1n
xn
+ xn+1
= - b1,
-a21 x1 - a22 x2 - - a2n xn + xn+2 = - b2,
(2.12)
-am1 x1 - am2x2 - - amn xn + xn+m = - bm.
Далее задача решается двойственным симплекс-методом. Этот метод применяется, тогда когда имеются базисные переменные в ограничениях-равенствах, все коэффициенты ЦФ положительны, ЦФ минимизируется, а среди правых частей ограничений имеется хотя бы одно отрицательное значение. Алгоритм двойственного симплекс-метода рассмотрен в п. 2.6.
Случай 3. Ограничения имеют вид равенств, ЦФ минимизируется.
a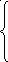
11
x1
+
a12
x2
+
+ a1n
xn
= b1,
a21 x1 + a22 x2 + + a2n xn = b2,
(2.13)
am1 x1 + am2 x2 + + amn xn =bm,
х i 0,
Q = P1 x1 + P2 x2 + + Pn xn min.
К такому виду сводятся все задачи линейного программирования, т.е. этот случай является общим.
Существует несколько методов приведения таких задач к каноническому виду. Один из них – метод искусственного базиса.
2.5.1. Метод искусственного базиса
Рассмотрим суть метода. Вводятся искусственные переменные xn+1, xn+2,, xn+m . Эти искусственные переменные добавляются к левым частям ограничений:
a
11
x1
+
a12
x2
+
+ a1n
xn
+ xn+1
= b1,
a21 x1 + a22 x2 + + a2n xn + xn+2 = b2, (2.14)
am1 x1 + am2 x2 + + amn xn + xn+m = bm.
Вводится искусственная целевая функция:
Q = xn+1 + xn+2 + + xn+m min,
xi
0, i =
1,(n+m).
Полученная задача приведена к каноническому виду. В ней искусственные переменные являются базисными. Далее эта задача решается симплекс-методом.
Чтобы ограничения остались прежними, в результате решения должны быть получены нулевые значения искусственных переменных и искусственной целевой функции.
Отметим особенность решения: если в процессе решения искусственная переменная переходит из базисной в свободную, то столбец, соответствующий этой переменной, исключается из рассмотрения, т.к. эта переменная становится равной нулю.
Анализ полученного решения:
1. Оптимальное решение полученной целевой функции положительно. В этом случае задача не имеет решения.
2. Оптимальное решение полученной целевой функции равно нулю и среди базисных переменных нет ни одной искусственной.
В итоге все исходные переменные оказались поделенными на две группы: свободные и базисные. В этом случае осуществляется переход к искомой целевой функции. Для этого в исходном выражении целевой функции базисные переменные выражаются через свободные.
Пример 2.4.
3
x1
+ 2 x3
- x5
= 12,
x1 - x2 + x3 = 5,
x1+ x3 + x4 = 6,
Q = 2 x1 + x2 - x3 + 3 x4 - x5 min.
Решение
1. Вводим искусственные переменные x6, x7, x8:
3
x1
+ 2 x3
- x5
+ x6
= 12,
x1 - x2 + x3 + x7 = 5,
x1+ x3 + x4 + x8 = 6.
Искусственная целевая функция G = x6 + x7 + x8 0, G = x6 + x7 + x8 = = 12 - 3 x1 – 2 x3 + x5 + 5 - x1 + x2 - x3 + 6 - x1- x3 - x4 = 23 – 5 x1 + x2 - 4 x3 - - x4 + x5 min.
2. Составляем симплекс таблицу:
-
1
2
3
4
5
63
0
2
0
-1
12
7
1
-1
1
0
0
5
8
1
0
1
1
0
6
-5
1
-4
-1
1
-23
Далее по симплекс-методу находим разрешающий элемент (3). Меняем местами переменные x1 и x6, причем столбец, соответствующий x6, вычеркиваем из таблицы.
Новая симплекс-таблица:
-
2
3
4
5
1
0
2/3
0
-1/3
4
7
-1
1/3
0
1/3
1
80
1/3
1
1/3
2
1
-2/3
-1
-2/3
-3
Теперь свободной становится переменная x8, следовательно, вычеркивается соответствующий столбец:
-
2
3
5
1
0
2/3
-13
4
7-1
1/3
1/3
1
4
0
1/3
1/3
2
1
-1/3
-1/3
-1
Из равноценных столбцов желательно выбрать такой,
чтобы искусственная переменная стала свободной.
В результате всех преобразований получена следующая таблица:
-
2
3
1
-1
1
5
5
-3
1
3
4
1
0
1
0
0
0
Как видно из таблицы, в результате тождественного преобразования исходные переменные разделены на базисные и свободные.
3. Переходим к исходной целевой функции:
Q = 2 x1 + x2 - x3 + 3 x4 - x5 .
Запишем ограничения, полученные из итоговой симплекс-таблицы:
x
1
- x2
+ x3=
5,
x5 – 3 x2 + x3 = 3,
x4+ x2 = 1.
Выразим базисные переменные через свободные и подставим эти выражения в целевую функцию:
Q = 2 x1 + x2 - x3 + 3 x4 - x5 =
= 2(5 + x2 – x3 ) + x2 - x3 + 3(1 – x2) – (3 +3 x2 - x3) = 10 - 3x2 - 2x3 .
В итоге получена начальная симплекс-таблица, т.е. задача приведена к каноническому виду:
-
2
3
1
-1
1
5
5
-3
1
3
4
1
0
1
-3
-2
-10